Моделирование алгебры высказываний с помощью релейно-контактных схем
Релейно-контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакты могут быть размыкающими и замыкающими. Каждый контакт подключен к некоторому реле. Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие - разомкнуты.
Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замыкающие контакты, подключенные к реле х, будем обозначать x1, ... xn, а размыкающие - 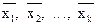 .
.
Всей схеме также можно поставить одно из двух значений 1, если схема проводит ток, и 0, если не проводит. Это значение есть функция переменных хi, 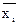 , т.е. логическая функция. Эту функцию называют функцией проводимости электрической цепи.
, т.е. логическая функция. Эту функцию называют функцией проводимости электрической цепи.
Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И наоборот, для некоторой схемы можно указать ее функцию проводимости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основные логические связки моделируются следующими элементарными схемами:
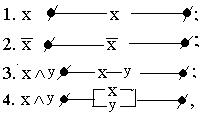
т.е. дизъюнкция моделируется параллельным соединением проводников, конъюнкция - последовательным.
Упражнение
Построить функцию проводимости следующей схемы:
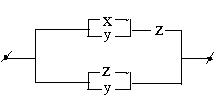
Рис. 5.1
Функция проводимости для такой схемы задается, очевидно, следующей таблицей:
Таблица 5.2
| x | y | z | f(x,y,z) |
По данной логической функции построим формулу - СКНФ:
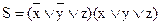
Упростим это выражение: 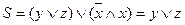 .
.
Построим более простую схему, имеющую ту же функцию проводимости, что и исходная:
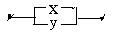
Рис. 5.2
Чтобы упростить релейно-контактную схему, не обязательно строить ее функцию проводимости. Можно написать соответствующую данной схеме формулу и упростить. Затем построить схему электрической цепи, моделирующую эту упрощенную формулу. Так, для электрической цепи, приведенной в данном примере,
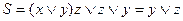 .
.
Дата добавления: 2016-01-26; просмотров: 1027;
