Работа сил, действующих на тело, и его кинетическая энергия
При переходе от рассмотрения движения материальной точки к рассмотрению движения тела законы Ньютона претерпели лишь небольшие уточнения. Иначе обстоит дело с понятиями «работа» и «кинетическая энергия». Поясним это на следующем примере.
Пример
Пусть человек сжимает двумя руками резиновый мяч, прикладывая к нему одинаковые по величине и противоположные по направлению силы (рис. 5.8).

Рис. 5.8.Работа, совершенная при сжатии мяча, отлична от нуля
Перемещение каждой руки направлено в сторону приложенной силы. Поэтому каждая рука совершила положительную работу. В тоже время мяч остался на месте, и его кинетическая энергия не изменилась (осталась равной нулю). Видимым результатом действия сил явилось лишь изменение его формы. Соотношение (4.8) между работой и кинетической энергией в этом случае не выполняется!
Кинетическая энергия тела, движение которого не является поступательным, тоже нуждается в уточнении, так как скорости точек тела различны.
Введем поправки и уточнения, необходимые для получения формул, которые можно использовать в практических расчетах.
Механической работойсилы, действующей на тело, называется скалярная величина, равная произведению силы на путь, пройденный точкой, к которой она приложена и на косинус угла между направлением силы и направлением движения этой точки:
A = F·s·соs(а). (5.8)
При вычислении кинетической энергии ограничимся рассмотрением движения твердого тела, т. е. тела, которое не изменяет форму и размеры. В этом случае кинетическая энергия равна сумме двух слагаемых:

где vцм —скорость движения центра масс тела, а евр — кинетическая энергия, связанная со вращением тела относительно центра масс. Формула для вычисления кинетической энергии вращения вокруг центра масс будет приведена в подразделе (7.1 ).
При поступательном движении тела скорости всех его точек одинаковы (v), а вращение отсутствует (Евр = 0). Поэтому кинетическая энергия при поступательном движении рассчитывается так же, как для материальной точки
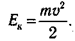
Связь между изменением кинетической энергии и работой внешних сил для твердого тела такая же, как для материальной точки:
Изменение кинетической энергии твердого тела равно сумме работ всех действующих на него внешних сил:
Fk2 – Fk1 = AI +AII + … (5.10)
Мощность
Даже очень маленькая сила при большом перемещении тела может совершить значительную работу. Правда, для этого потребуется немалый промежуток времени. Однако во многих случаях величина участка траектории и время действия силы ограничены. Например, при прыжке сила мышц действует только при разгибании сустава достаточно малое время. За это время работа мышц должна успеть сообщить прыгуну необходимую кинетическую энергию. Поэтому важной характеристикой «устройств», используемых для совершения работы является скорость ее совершения. Такая характеристика называется мощностью.
Полезной мощностью называется скалярная величина, равная отношению работы ко времени, за которое она совершена:

Затраченной мощностью (мощность энергозатрат) называется скалярная величина, равная отношению затраченной энергии ко времени, за которое она израсходована:
P3= 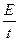 (5.12)
(5.12)
Формулы (5.11 и 5.12) определяют среднюю мощность. Для анализа практических ситуаций этого понятия не достаточно. Например, при спурте (англ. spurt — рывок) спортсмен должен за относительно малое время набрать большую скорость и способность к спурту у разных людей различна. Поэтому вводят понятие мгновенной мощности.
Мгновенной мощностью называют отношение работы (dA) ко времени, вычисленное для очень малого интервала (dt):

Аналогично определяется мгновенная мощность энергозатрат:

Отношение полезной мощности к затраченной показывает насколько эффективно используется энергия и называется коэффициентом полезного действия (КПД), который выражают в процентах:
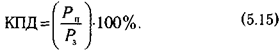
Единица измерения мощности в СИ называется Ватт: 1 Вт = ДЖ/с (т. е. 1 Вт — это мощность двигателя, который совершает работу 1 Дж за 1 с).
Если двигатель используется для перемещения тел, то мощность (Р), сила тяги (FT) и скорость движения (v) связаны соотношением:
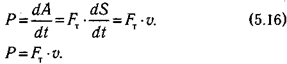
Дата добавления: 2015-11-28; просмотров: 1243;
