Пропускная способность газопровода

Особенностью работы МГ является сжимаемость транспортируемой среды. Перемещение газа по трубопроводу связано с преодолением сил трения, что приводит к снижению его давления. При снижение давления плотность газа уменьшается и при постоянном массовом расходе это приводит к увеличению объемной производительности и скорости течения газа.

Газ после компримирования имеет температуру, значительно превышающую температуру грунта и перемещение его по трубопроводу сопровождается снижением температуры, что вызывает повышение плотности, Давление газа на участке между КС снижается в 1,45-1,50 раза. Температура при этом максимально может измениться от 325 К до 273 К, то есть менее чем в 1,2 раза. Таким образом, объемная производительность газа в участке, а, следовательно, и скорость его течения возрастет более чем в 1,45: 1,2 = 1,2 раза. Возрастание скорости течения газа сопровождается увеличением потерь давления на преодоление сил трения и переходом части потенциальной энергии в кинетическую. Отсюда можно сделать вывод о том, что при движении газа по участку между КС потери давления на единице длинны трубопровода возрастают и линия изменения давления газа по длине участка не будет прямой.

Скорость распространения звука в МГ составляет величину порядка 450 м/с.

При отключении и подключении КС или потребителя в газопроводе возникает нестационарный режим течения газа. Продолжительность нестационарного режима определяется временем перехода МГ от одного стационарного состояния к другому и связана со скоростью распространения волн изменения давления по длине газопровода. Волны изменения давления перемещаются со скоростью распространения звука в газе, которая составляет порядка 450 м/с. Так при длине газопровода 100 км время прохождения волны составит порядка 4 мин. Так как время нестабильной работы МГ значительно меньше времени стабильной работы, то при проектировании и эксплуатации газопроводов их рассчитывают как условно стационарные.

Для вывода уравнения пропускной способности МГ можно воспользоваться двумя уравнениями: уравнением движения газа и уравне­нием неразрывности.

Уравнение неразрывности для постоянного массового расхода 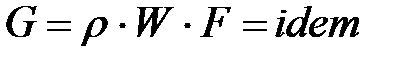, (1.23) в дифференциальной форме 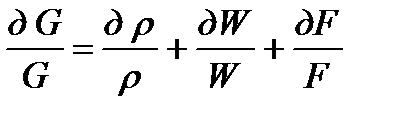. Поскольку газ является сжимаемой средой, то с удалением от компрессорной станции его плотность уменьшается и давление падает. Это приводит к росту скорости движения газа.

Уравнение баланса удельной энергии в дифференциальной форме будет выглядеть

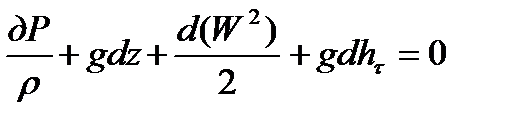(1.22).

где r, W, P - плотность, скорость течения и давление газа на расстоянии х от начала участка в момент времени t;

z - высота, на которой находится ось трубопровода в точке х;

g - ускорение свободного падения;

dh_τ – работа по преодалению сил трения

Установим физический смысл уравнения (1.22), для чего определим на примере члена в левой части единицу измерения членов его составляющих:

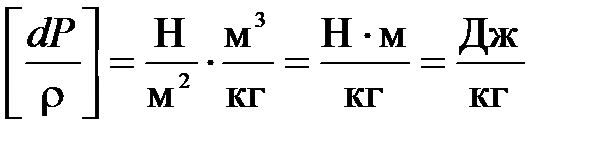
Таким образом, каждый член уравнения представляет собой удельную работу (удельную энергию), соответственно, изменения давления, преодоления сил трения, изменения скорости течения газа, преодоления силы тяжести.

Выражение (1.22) является уравнением баланса энергии установившегося потока газа в дифференциальной форме. Оно справедливо для сжимаемой и несжимаемой жидкости.

В реальных условиях МГ затраты энергии на изменение скорости течения газа значительно меньше общих затрат и ими пренебрегают (задача 1.3).

В условиях МГ в большинстве случаев можно пренебречь изменение кинетической энергии - 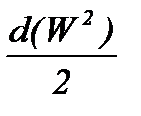. В большинстве случаев МГ проходят по относительно мало пересеченной местности и разность геодезических отметок не превышает 100 м. В соответствии с ОНТП такие газопроводы рассчитываются как горизонтальные, и разностью геодезических отметок 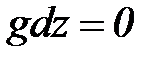. Тогда уравнение удельной энергии (1.22) приобретет вид:

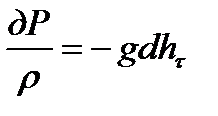(1.19)

Для решения уравнения 1.19 в случае изотермического установившегося движения воспользуемся уравнением состояния 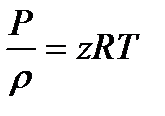, в уравнении (1.23) 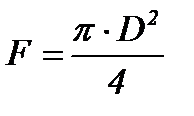. Используем уравнение Дарси-Вейсбаха для определения потери напора ,

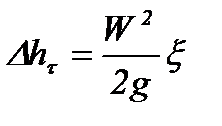где - 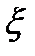коэффициент местного сопротивления, для участка трубы он равен ,

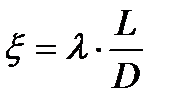где - 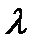- коэффициент потерь на трение, D- внутренний диаметр трубопровода.

Тогда для участка трубы потери напора составят:

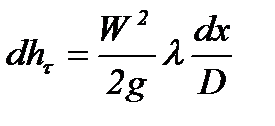(1.20).

Подставим в уравнение 1.19 уравнение 1.20

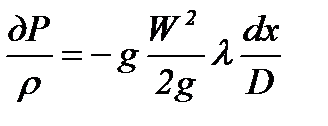, выразим 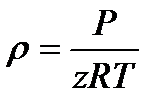и подставим 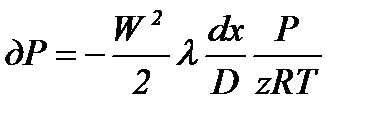(1.24)

Выразим скорость потока через уравнение неразрывности 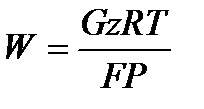и подставим в 1.24.

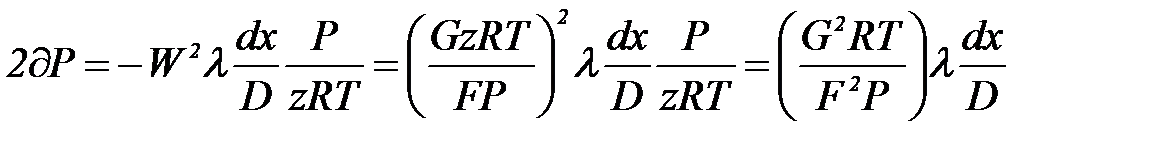
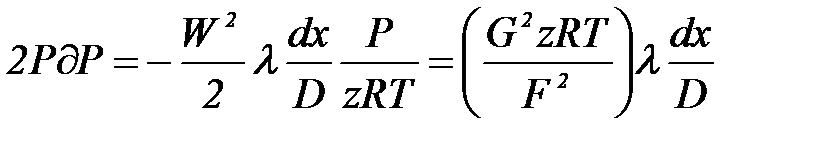(1.27)

Приняв l = idem, T=T_cp=idem, z=z_cp=idem проинтегрируем 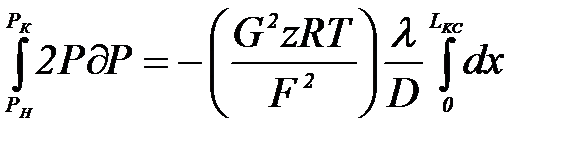и получим 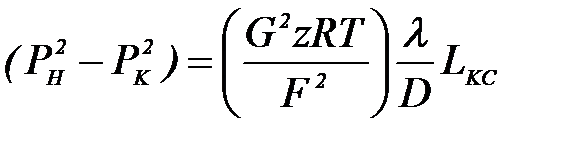(1.28)

где Р_Н, Р_К - давление газа в начале и в конце участка (абсолютное). Па;

Т - средняя температура газа в участке. К;

Z - среднее значение коэффициента сжимаемости газа в участке;

L_КС - длина участка, м ;

F - площадь поперечного сечения трубопровода, м²;

D - внутренний диаметр трубопровода, м.

Решим (1.28) относительно массовой производительности, выразив предварительно площадь поперечного сечения через диаметр

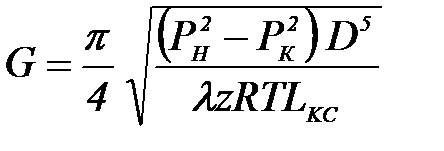. (1.29)

Как уже было сказано ранее, расчетной величиной при проектировании и эксплуатации МГ является объемная суточная производительность, приведенная к стандартным условиям.

Разделив (1.29) на плотность газа при стандартных условиях и выразив газовую постоянную газа через газовую постоянную воздуха , получаем

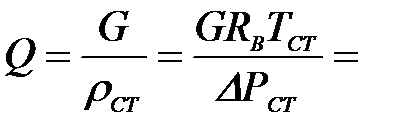
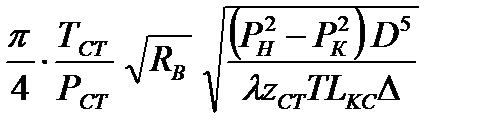, (1.30)

где Q - объемная пропускная способность участка, м³/ с.

Стоящие перед корнем величины являются постоянными и их можно объединить в один коэффициент с 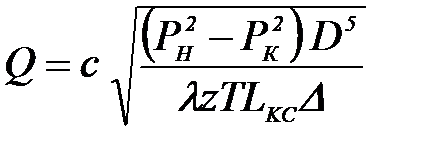, (1.31)

где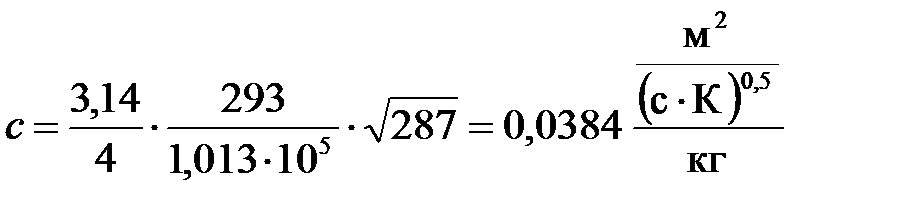

На практике удобно использовать производительность в млн. м³/сут, давление в МПа и длину участка в км. В этом случае коэффициент с будет учитывать помимо величии указанных выше еще и переходные коэффициенты и его значение составит 105,087.

ЛЕКЦИЯ 2.