Закон Архимеда. Плавание тел
Описанный выше способ определения вертикальной составляющей силы давления на криволинейную поверхность можно использовать для доказательства закона Архимеда.
Рассмотрим силы, действующие на погруженное в жидкость тело произвольной формы (рис. 3.17).Спроектируем это тело на свободную поверхность жидкости и построим проектирующую цилиндрическую поверхность АБВГА'Б'В'Г', касающуюся поверхности тела. Соединим точки касания цилиндрической поверхности с поверхностью тела и получим кривую АБВГ, которая разделяет поверхность тела на верхнюю и нижнюю части. Также разделим тело аналогичным образом вертикальной плоскостью и получим кривую БДГИ. В результате тело оказывается разделенным на четыре части – I, II, III и IV. На наружные поверхности этих частей действуют соответствующие вертикальные F 'В1…4 и горизонтальные составляющие F 'Г1…4 сил давления.Очевидно, что горизонтальные составляющие F 'Г1 и F 'Г2 равны по модулю и противоположны по направлению (см. подраздел 3.6). Такой же вывод можно сделать и силах F 'Г3 F 'Г4. Таким образом, равнодействующая горизонтальных составляющих сил давления будет равна нулю.


Вертикальная составляющая силы гидростатического давления F 'В1 направлена вертикально вниз и равна:
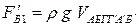 .
.
СилаF 'В2 также направлена вертикально вверх и определяется зависимостью:
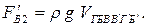
Равнодействующая силF 'В1 и F 'В2 будет направлена вертикально вниз и равна
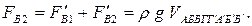 (3.32)
(3.32)
Проведя аналогичные выводы, получим зависимость для расчетаFВ1. Эта сила будет направлена вертикально вниз.
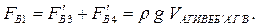 (3.33)
(3.33)
Так какF В1 > F 'В2, то равнодействующая силFВ1 и FВ2 будет направлена вертикально вверх и равна
 (3.34)
(3.34)
Объем VАИВДБГ является объемом тела VТ, погруженного в жидкость. Окончательно
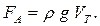 (3.35)
(3.35)
СилаFА называется силой Архимеда и является выталкивающей силой. Данное положение является законом Архимеда,который формулируется следующим образом: на тело, погруженное в жидкость, действует выталкивающая сила, численно равная весу жидкости, вытесненной телом, направленная вертикально вверх и приложенная в центре масс вытесненного объема. Это современная формулировка закона. Во второй книге трактата «О плавающих телах» в предложении 7 Архимед сформулировал этот закон следующим образом: «Если более тяжелое, нежели жидкость, тело будет в нее помещено, то оно опустится на дно, и его вес в жидкости уменьшится на столько, сколько весит жидкость в объеме, равном объему тела». Кроме того, в постулате 2 он писал: «Мы предполагаем, что сила, которою плавающее в жидкости тело поддерживается, направлена вертикально вверх и проходит через его цент тяжести» [4, с. 353].
На данное тело действует также сила тяжести G (см. рис. 3.17). В зависимости от соотношения сил FА и G возможны три случая положения тела:
- FА > G – тело всплывает и плавает на поверхности жидкости в частично погруженном состоянии (вес жидкости, вытесненный погруженной частью тела, равен весу тела);
- FА < G – тело тонет;
- FА = G – тело плавает в полностью погруженном состоянии.
Дата добавления: 2016-01-26; просмотров: 998;
