Сумісна дія згину та кручення.

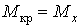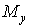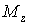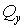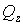Круглі вали. Сили, що діють на вали (тиск на зуби шестірень, натяг ременів, власна вага вала й шківів і т.п.), викликають у поперечних перерізах валів наступні внутрішні силові фактори: ; ; ; і . Таким чином, у будь-якому поперечному перерізі одночасно виникають нормальні напруження;tyyz від вигину у двох площинах, а також дотичні напруження від крутіння й вигину.

Для розрахунку вала в першу чергу необхідно встановити небезпечні перерізи. Із цією метою повинні бути побудовані епюри згинальних моментів 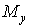, 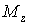і крутного моменту .

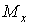Навантаження, що діють на вал, розкладаємо на складові уздовж координатних осей (рис. 10.29), а потім будуємо епюри: від сил 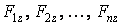- епюру 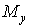, від сил 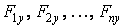-епюру 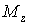(рис.5, б и в).

А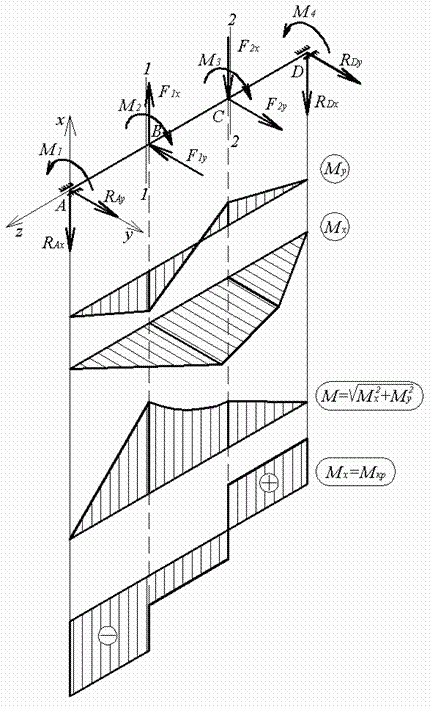
Б
В
Г
д

Рис. 5. Вигин із крутінням вала

При вигині вала круглого або кільцевого перетину в кожному з його перетинів має місце прямий вигин під дією результуючого згинального моменту

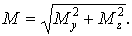
(4)

Вектор моменту М у різних перетинах може мати різні напрямки, у силу чого навіть при відсутності розподілених навантажень епюра М може бути криволінійною (рис. 5, г). Для загального випадку це легко показати аналітично.

Нехай 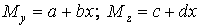(a, b, з, d — постійні коефіцієнти). Тоді

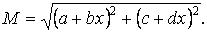
Вираз, що стоїть під радикалом, лише в деяких окремих випадках є повним квадратом (наприклад, при 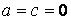), а в більшості випадків епюра криволінійна, причому

Це дозволяє будувати епюри М спрощеним способом, трохи завищуючи значення сумарного згинального моменту М на ділянках між переломами епюри: величини сумарного згинального моменту М обчислюють лише для тих перетинів, у яких на епюрах 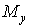і 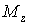є переломи. Ці величини відкладають у масштабі по одну сторону від осі на епюрі М и з'єднують прямою лінією.

Далі будуємо епюру 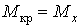(рис. 5, д) і шукаємо небезпечні перерізи, у яких одночасно великі M і 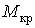. Зіставляючи епюри, знаходимо, що небезпечним буде перетин 1 — 1 або 2 — 2.

Тепер у небезпечному перерізі потрібно знайти небезпечні точки. Визначаємо положення нейтральної лінії і будуємо епюру нормальних напружень від результуючого згинального моменту М (рис. 6), які змінюються пропорційно відстані точок від нейтральної лінії. Очевидно, небезпечними є точки A і В, найбільш вилучені від нейтральної лінії, — у них одночасно і нормальні напруження від вигину і дотичні напруження мають найбільші значення:

	(5)
	(6)

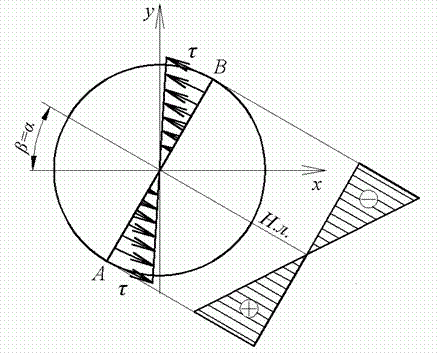
Рис. 6. Епюра нормальних напружень

У найнебезпечнішої точки У виділимо елемент (рис. 7) По чотирьох його гранях діють дотичні напруження, а до двох із цих граней прикладені ще й нормальні напруження. Інші дві грані вільні від напружень. Таким чином, при вигині із крутінням елемент у небезпечній точці перебуває в плоскому напруженому стані.

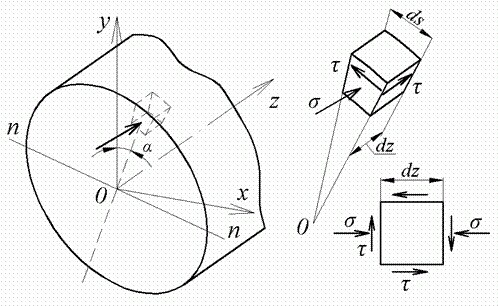
Рис. 7. Елемент вала при вигині із крутінням

Зовсім аналогічними були напруження на гранях у брусі який згинається, тому тут головні напруження потрібно визначати по тим же формулам:

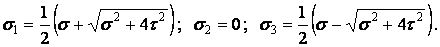
(7)

Різниця між виразами (6) і (7) лише в тім, що в останньому випадку дотичні напруження викликаються крутним моментом, а при вигині вони викликалися поперечною силою.

Помітимо, що в цьому випадку складного напруженого стану впливом дотичних напружень від поперечних сил зневажаємо, тому що вони значно менше дотичних напружень, викликаних крутінням.

Для перевірки міцності елемента, виділеного в небезпечної точці потрібно, вибравши відповідну теорію міцності:

по теорії Мору

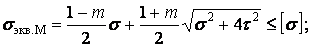
(8)

по IV теорії

(9)

Підставляючи у формули (8), (9) вираз для напружень і з огляду на, що , одержимо

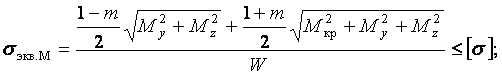
	(10)
	(11)

Чисельники цих формул являють собою наведені моменти, дія яких еквівалентно спільній дії трьох моментів (відповідно до прийнятої теорії міцності). Отже,

	(12)
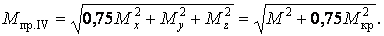
	(13)

Якщо буде потреба подібним же чином можна одержати формули для наведених моментів і по інших теоріях міцності.

Неважко помітити, що тепер умови міцності можна замінити однією простою формулою

(14)

Таким чином, при спільній дії вигину із крутінням стрижні круглого перетину розраховують на вигин від приведеного моменту М_пр.

Вирішуючи нерівність (14) відносно W, одержуємо формулу для визначення моменту опору:

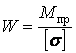
(15)

і діаметра круглого вала:

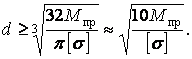
(16)

Помітимо, що наведені формули повністю застосовні і до стрижнів кільцевого перетину.

Розглянемо найпростіший приклад розрахунку вала на вигин із крутінням.

Приклад 1. На вал (рис. 8) насаджені три зубчасті колеса. Колеса навантажені силами 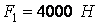; ; 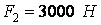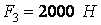, причому сила 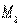вертикальна, а сил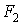и й 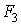горизонтальні. Діаметри зубчастих коліс наступні: ; ; 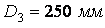. Допустиме напруження 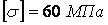. Підібрати діаметр вала по четвертій теорії міцності.

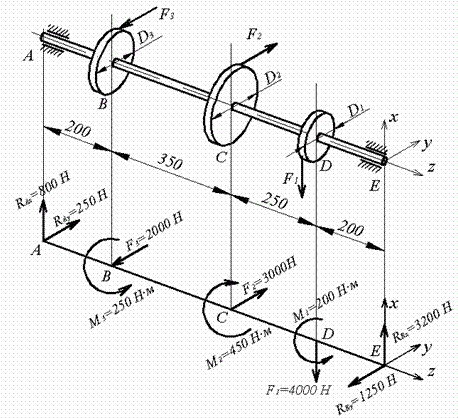
Рис. 8. До прикладу 1

Замінимо навантаження статично еквівалентною системою сил.

Перенесемо сили , і 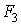на вісь вала, заміняючи кожну з них силою, прикладеної в точці В, З або D відповідно, і парою, що скручує, 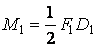сил 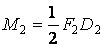; ; 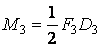відповідно. Таким чином, одержуємо розрахункову схему (рис. 10.32). На схемі зазначені як значення прикладених зовнішніх навантажень 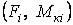, так і величини викликаних ними опорних реакцій.

Розглядаючи окремо сили в горизонтальній і вертикальній площинах (рис.9, а й б), будуємо епюри згинальних моментів. Для побудови сумарної епюри моментів М обчислюємо ординати в характерних точках по формулі :

у перетині В

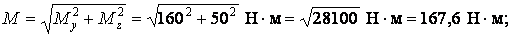
у перетині C

у перетині D

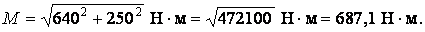
а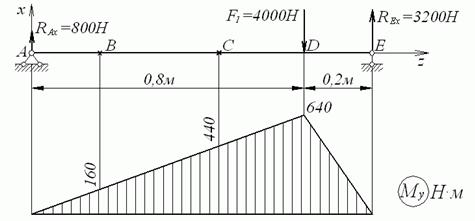
б
в
г

Рис. 9. Побудова епюр до прикладу 1

Епюра М, побудована за цим даними, наведена на рис. 9, в. Як вказувалося раніше, на ділянках ВР і CD такаючи епюра має завищені значення ординат (дійсні значення показані штриховою лінією).

Розглядаючи діючі на вал моменти, будуємо епюру крутних моментів (рис. 9, г).

Зіставляючи епюри M і 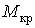, знаходимо, що небезпечним є перетин 1 – 1, розташований ліворуч від точки С, де одночасно діють 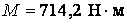і .

Згідно IV теорії міцності, наведений момент обчислимо по формулі (13). Одержимо

Підставляючи наведений момент у формулу (15), знаходимо необхідний осьовий момент опору:

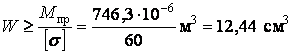
і, поклавши 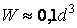, обчислюємо необхідний діаметр вала:

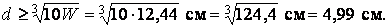
Округливши до найближчого стандартного діаметра, приймаємо .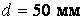

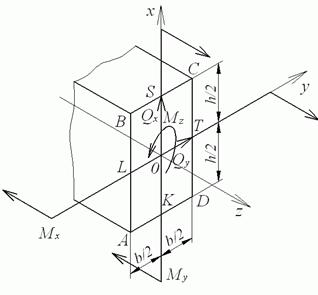
Брус прямокутного перетину. На практиці часто зустрічаються стрижні некруглого перетину, піддані дії крутних і згинальних моментів. Як приклад розглянемо брус прямокутного перетину (рис. 10, а), навантажений силами й , що викликають у поперечних перерізах згинальні момент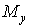и й 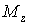, а також поперечні сил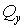и й .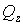

а
б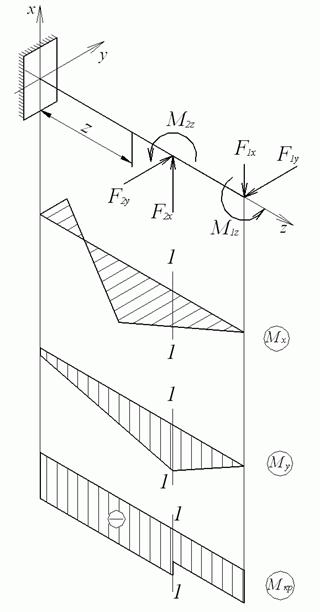

Рис. 10. Брус прямокутного перетину

Розрахунок виконуємо в такій послідовності. Розкладаємо задані навантаження (сили й ) на складові уздовж координатних осей і приводимо їх до осі вала; при цьому одержуємо в поперечних перерізах, у площинах яких перебувають точки прикладання сил, зовнішні моменти, що скручують, і . Отримана в такий спосіб розрахункова схема представлена на рис. 10.

Для того щоб установити положення небезпечного переріза, будуємо епюри згинальних моментів 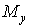і 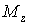, а також епюру крутних моментів 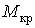(рис. 10, б).

Зіставлення епюр показує, що найнебезпечнішим є перетин 1 — 1 бруса, розташований ліворуч точки прикладання сили 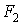. У цьому перетині діють найбільші згинальні моменти 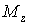, 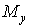і максимальний крутний момент 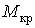. Щоб перевірити міцність бруса, потрібно в небезпечному перерізі знайти небезпечну точку, обчислити для неї еквівалентне напруження (по одній з теорій міцності) і зіставити його з допустимим напруженням, що.

Для знаходження небезпечної точки перетину будуємо епюри напружень від всіх силових факторів (рис. 11, б-е): ; ; ; ; .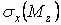

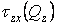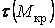Епюра 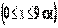для довгої сторони контуру має максимум, що позначимо 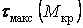. Найбільшу ординату епюри 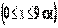на короткій стороні позначимо 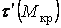. Ці напруження можна розрахувати по відомих формулах крутіння брусів прямокутного перетину:

(17)

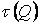Епюри нормальних і дотичних напружень наочно показують, що на відміну від круглого перетину в розглянутому випадку найбільші нормальні напруги й найбільші дотичні напруження й 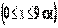мають місце не в одній і тій же точці.

а	б	в
г	д	е

Рис. 12. Епюри напружень

Отже, для виявлення самої небезпечної точки в перетині; потрібно зіставити еквівалентні напруження в декількох небезпечних точках. Звичайно вважають достатнім розглянути три точки перетину: одну кутову точку (A або С), одну точку посередині довгої сторони прямокутника (L або Т) і одну точку посередині короткої сторони прямокутника (S або K).

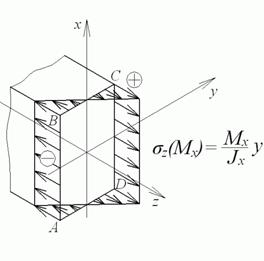
Елемент, виділений в околиці точки С (при прийнятих на рис. 12, а напрямках М_у й M_z), перебуває в умовах простого розтягання напруженнями, рівними сумі нормальних напружень від М_у й M_z. Тому умова міцності для цієї точки повинна бути записана як для випадку лінійного напруженого стану:

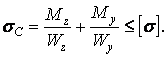
(18)

Елемент в околиці точки А також перебуває в умовах лінійного напруженого стану — простого стиску, тому що 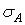відрізняється від 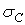тільки знаком. Якщо матеріал бруса має різні допустимі напруження, що, для розтягання й для стиску, то перевіряти міцність по формулі (18) необхідно в кожній із цих точок.

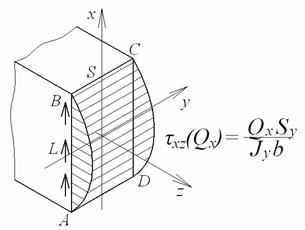
Елементи в околиці точок L і K перебувають у плоскому напруженому стані, і, отже, головні напруження в них, як і в круглому брусі, можна обчислити по формулі (7). У загальному випадку дотичні напруження, що входять у формулу (7), варто обчислювати як від дії крутного моменту 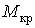, так і від дії поперечних сил:

(19)

Однак дотичні напруження від поперечних сил Q_y і Q_z, як відзначалося, звичайно мале, а тому в більшості випадків їх впливом можна зневажити.

Для обчислення еквівалентних напружень у точках L і K підставляємо значення нормальних і дотичних напружень у формули (8) і (9). Одночасно одержимо і відповідні умови міцності (по IV теорії й по теорії Мору):

у точці L

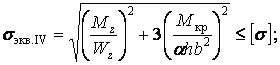
	(20)
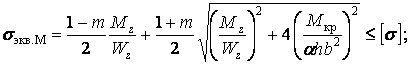
	(21)

у точці K

	(22)
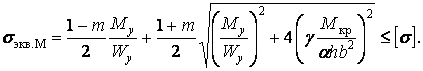
	(23)

Знаки моментів при підстановці їх у рівняння (20) – (23) не мають значення, тому що в ці формули входять квадрати моментів.

Таким чином, найнебезпечніша точка визначається тільки в результаті обчислення еквівалентних напружень у всіх трьох точках (З, L і K) по формулах (18) і (20) — (23), причому в кожному окремому випадку положення найнебезпечнішої точки залежить від конкретного співвідношення величин моментів 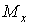, 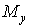і .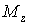
Питання для самоконтролю

1. Дайте визначення косого згину.

2. Напишіть формулу для визначення нормальних напруг у попереч­ному перерізі бруса при косому згині.

3. Як визначити положення нейтральної лінії при косому згині?

4. Як визначити положення нейтральної лінії при позацентровому розтягу /стиску/?

5. Як визначити небезпечний переріз вала при згині з крученням? Який напружений стан виникає в поперечному перерізі?

6. Розкрийте, сутність проектного і перевірного розрахунків на міцність вала при згині з крученням.

Заняття № 64