Пересечение линии второго порядка с прямой. Асимптотические направления. Классификация линий второго порядка по числу и действительности асимптотических направлений.

Предположим, что относительно ОДСК задана линия второго порядка общим уравнением .

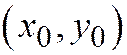Будем искать пересечение этой линии с прямой, уравнения которой возьмём в параметрической форме: , . Здесь - некоторая точка прямой, а - её направляющий вектор. Для нахождения координат точек пересечения прямой , с линией (1) надо найти значения параметра , при которых точка прямой лежит на линии (1). Подставляя в уравнение (1) и , получим:

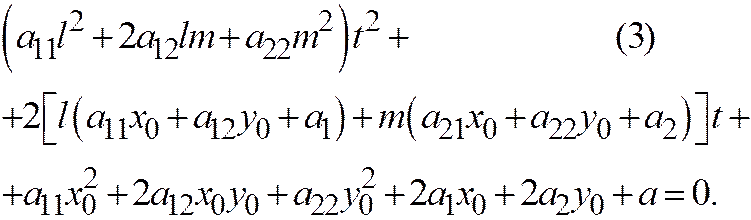
Если в этом уравнении коэффициент при отличен от нуля, то уравнение (3) имеет два корня (действительных различных, мнимых различных, или действительных совпадающих), и, значит, прямая линия пересекает линию (1) в двух точках (соответственно действительных различных, комплексных сопряжённых, или действительных совпадающих).

Если же 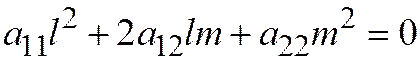, (4)

то прямая с направляющим вектором 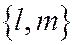либо пере-секает линию второго порядка только в одной точке (это будет тогда и только тогда, когда коэффициент при в уравнении (3) равен нулю, а коэффициент при не равен нулю); либо не пересекает её (это бу-дет тогда и только тогда, когда коэффициенты при и в уравнении (3) равны нулю, а свободный член не равен нулю); либо входит в состав данной линии (это будет тогда и только тогда, когда соотношение (3) яв-ляется тождеством относительно ).

Определение. Говорят, что прямая имеет асимптотическое направление по отношению к данной линии второго порядка, если координаты 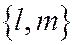её направляющего вектора удовлетворяют уравнению 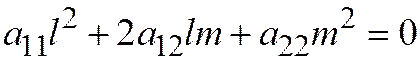. Говорят также, что вектор 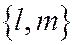имеет асимптотическое направление.

По отношению к асимптотическим направлениям линии второго порядка делятся на три типа:

А. Линии эллиптического типа: это линии второго порядка, не имеющие асимптотических направлений (эллипс, мнимый эллипс, две мнимые пересекающиеся прямые).

В. Линии гиперболического типа, имеющие два асимптотических направления (гипербола, две пересекающиеся прямые).

С. Линии параболического типа; это линии, имеющие одно асимптотическое направление (парабола, две параллельные или совпадающие прямые).

Теорема 3. Необходимым и достаточным условием того, что линия второго порядка, заданная общим уравнением (1) относительно ОДСК не имеет асимптотических направлений (действительных), т.е. явля-ется линией эллиптического типа, является условие:

.

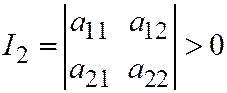Необходимым и достаточным условием того, что линия второго порядка, заданная общим уравнением (1) относительно ОДСК имеет два различных действительных асимптотических направления т.е. является линией гиперболического типа, является условие:

.

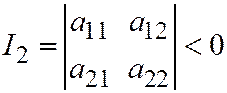Необходимым и достаточным условием того, что линия второго порядка, заданная общим уравнением (1) относительно ОДСК имеет только одно асимптотическое направление т.е. является линией параболического типа, является условие:

.

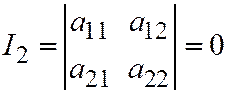Доказательство. Координаты вектора 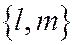, имеющего асимптотическое направление, определяются из уравнения .

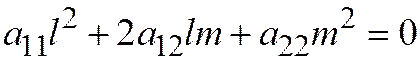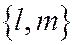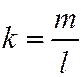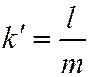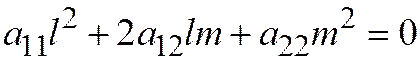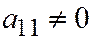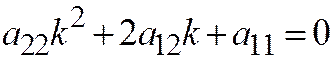Так как вектор ненулевой, то имеет смысл рассматривать по крайней мере одно из соотношений: ; или . Уравнение , следовательно, эквива-лентно одному из уравнений (или , или ):

; или .

Для того, чтобы решения любого из этих уравнений были комплексными (сопряжёнными), Действительными различными, или совпадающими, необходимо и достаточно, чтобы выполнялось, соответственно, условие ; ; .

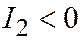В первом случае ( , при этом дискриминант квадратного уравнения 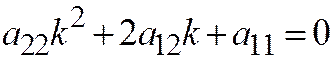: ), линия не имеет действительных асимптотических направлений и является линией эллиптического типа; во втором случае ( 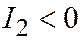, 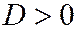), линия имеет два различных асимптотических направления и является линией гиперболического типа; в третьем случае ( , 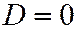), линия имеет одно (действительное) асимптотическое направление и является линией параболического типа. В последнем третьем случае угловой коэффициент 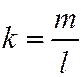единственного асимптотического направления определяется одним из соотношений: или .

Если , то асимптотическим направлением является направление оси , т.к. уравнение, определяющее координаты векторов, имеющих асимптотические направления 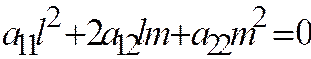, принимают вид: , откуда 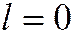. (Ну, напри-мер, возьмём параболу 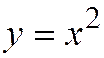, перепишем это урав-нение в виде . Здесь , 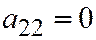. Но ведь мы с Вами хорошо знаем, что у параболы 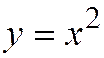асимптотическим направлением является направление оси .

Остаётся рассмотреть случай . Уравне-ние линии принимает вид: 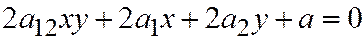, а уравнение, из которого находятся координаты векторов, имеющих асимптотические направления: 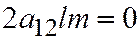, следовательно, либо , либо 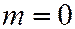, т.е. линия имеет два различных асимптотических направления - направления осей координат. (Заметим, что 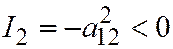, значит, линия гиперболического типа.

Обратно, если оси координат имеют асимптотичес-кие направления, то уравнение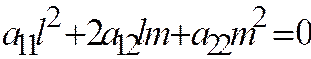

должно удовлетворяться и при , и при 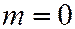, т.е. . Значит, уравнение линии имеет вид: .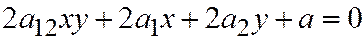

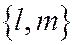Рассмотрим примеры. Для гиперболы или для двух пересекающихся прямых координаты векторов, имеющих асимптотические направления, определяются из уравнения 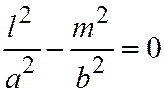, т.е. это, соответственно, или направления асимптот гиперболы, или (если это две пересекающиеся прямые) направления рассматриваемых прямых.

Для параболы 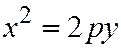уравнение, определяющее координаты вектора 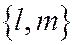асимптотического направления, имеют вид: 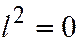, т.е. , значит, асимптотическое направление параболы есть направление её оси.

Если, наконец, уравнение линии второго порядка определяет две параллельные (или совпадающие) прямые, то асимптотическим направлением является направление этих прямых.