Вычисление объема тела по известным площадям его параллельных сечений
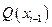
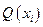


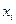
 x
x
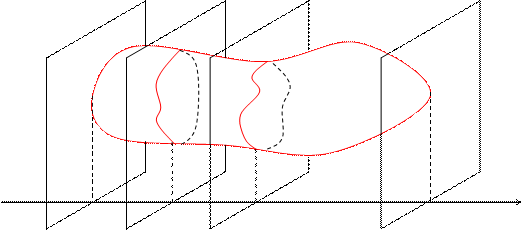
Рассмотрим тело с объемом V . Пусть известна площадь любого поперечного сечения тела Q, выражаемая непрерывной функцией 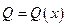 . Разобьем тело на “слои” поперечными сечениями, проходящими через точки
. Разобьем тело на “слои” поперечными сечениями, проходящими через точки 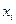 разбиения отрезка
разбиения отрезка 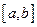 . На каждом отрезке разбиения
. На каждом отрезке разбиения 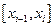 функция
функция 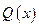 непрерывна. Следовательно, принимает на нем свои наибольшее и наименьшее значения. Обозначим их соответственно
непрерывна. Следовательно, принимает на нем свои наибольшее и наименьшее значения. Обозначим их соответственно 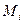 и
и 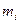 .
.
Если на этих наибольшем и наименьшем сечениях как на диаметрах построить цилиндры с образующими, параллельными оси  , то объемы этих цилиндров будут соответственно равны
, то объемы этих цилиндров будут соответственно равны  и
и  , где
, где  .
.
Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно 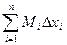 и
и 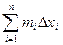 .
.
При стремлении к нулю шага разбиения наибольшего из отрезков разбиения l, эти суммы стремятся к общему пределу:
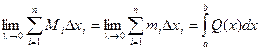
Таким образом, объем тела находится по формуле:
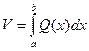
Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию 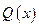 , что весьма проблематично для сложных тел.
, что весьма проблематично для сложных тел.
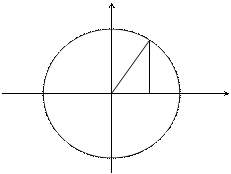
Пример. Найти объем шара радиуса R.
R y
-R 0 x R x
В поперечных сечениях шара получаются окружности переменного радиуса у. В зависимости от текущей координаты  этот радиус выражается по формуле
этот радиус выражается по формуле 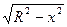 .
.
Функция площадей сечений имеет вид: 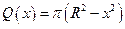 . Получаем объем шара:
. Получаем объем шара:
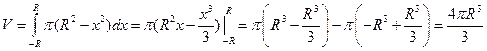 .
.
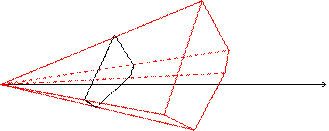
Пример. Найти объем произвольной пирамиды с высотой Н и площадью основания S.
 |
Q S
x H x
При пересечении пирамиды плоскостями, перпендикулярными высоте, в сечении получаем фигуры, подобные основанию. Коэффициент подобия этих фигур равен отношению 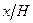 , где х – расстояние от плоскости сечения до вершины пирамиды.
, где х – расстояние от плоскости сечения до вершины пирамиды.
Из геометрии известно, что отношение площадей подобных фигур равно коэффициенту подобия в квадрате, т.е.
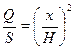 .
.
Отсюда получаем функцию площадей сечений: 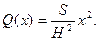
Находим объем пирамиды: 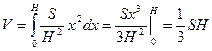 .
.
Дата добавления: 2015-11-28; просмотров: 991;
