Множество U, содержащее в себе все элементы рассматриваемых множеств, называется универсальным множеством.
Лекция Множества
Множество относится кпервоначальным понятиям науки, не определяемым через другие, более простые термины. Множество представляет собой определенную совокупность объектов, объединенных в единое целое в соответствии с некоторыми признаками и правилами.Множества обозначаются: A, B, C, X, Y, Z. Примеры множеств:
· множество всех атомов на Марсе;
· множество точек окружности;
· множество решений заданного уравнения;
· множество всех действительных чисел - R.
Г. Кантор (1845–1918 гг.) определял Множество как «многое, понимаемое как единое».
Наконец, определение Множества как «совокупности определенных различаемых объектов». Здесь для «объекта» важен просто сам факт принадлежностик Множеству – своеобразное характеристическое свойство.
Таким образом, в общем случае требуется задать характеристическое свойство, которым должны обладать все элементы множества. Способ задания «принадлежности», или попросту, путем перечисления годится, только для конечныхмножеств.
Множества обозначаются обычно большими латинскими буквами (необязательно), в их определении используется фигурные скобки ( {} ). Например, M = {a, b, c }.
Здесь определено 3-элементное множество путем простого перечисления элементов.
Еще пример, множество натуральных чисел: N= {1, 2, 3, …}.
Предметы (объекты), составляющие данное множество, называют его элементами.
Кстати, порядокэлементов множества роли не играет: {1, 2, 4} = {2, 1, 4}.
Это в отличие от набора (кортежа), где порядок важен и вместо фигурных скобок используются круглые: (1, 2, 4) ¹ (2, 1, 4).
Принадлежность элемента множеству символизируется знаком Î
(похоже на греческую букву e): 4 Î М, 3 Ï М.
Считается, что повторяющихся элементов во множестве быть не должно (в отличие опять же от кортежа).
Множество Æ, не содержащее ни одного элемента, называется пустым множеством Æ.
Пример . Множество решений уравнения x2 + 1 = 0 во множестве R – пустое множество Æ.
Множество U, содержащее в себе все элементы рассматриваемых множеств, называется универсальным множеством.
Важнейшей характеристикой множества является его мощность (размер, норма, длина). Это количество элементов множества. Например,
А = {1, 2, …, n} = {х : х Î N, 1 £ x £ n}, |А| = card (A) = n.
Множество – конечное, если оно пустое или если его элементы могут быть пронумерованы 1, …, n, n Î N. В противном случае множество –бесконечное.
Если каждый элемент множества А является вместе с тем и элементом множества В, то А называется подмножеством множества В:
А Í В - А содержится в В (или А включено в В) 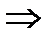 А подмножество В;
А подмножество В;
Если А Í В и А ¹ В, то А называется строгим (собственным) подмножеством множества В (обозначается А 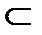 В).
В).
Свойства подмножества: Æ Í А, А Í А, А Í U.
Множества А и В называются равными, если каждый элемент множества А является вместе с тем и элементом множества В, и каждый элемент В является элементом А:
А = В  А
А 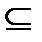 В и В
В и В 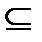 А.
А.
Для описания множеств будем использовать два способа:
1. Перечисление: A = ía, b, cý; X = íx1, x2, ¼, xný.
2. Задание множества с помощьюзаписи свойства, определяющего отношение принадлежности элементов данному множеству:
A = íx: F(x)ý - множеству А принадлежат все те и только те элементы х, которые обладают свойством F(x).
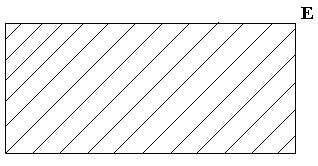 Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри него - кругов (или каких-либо других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств.
Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри него - кругов (или каких-либо других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств.
Универсальное множество на диаграмме Венна
Дата добавления: 2016-01-20; просмотров: 1278;
