Свойства векторного произведения векторов
Определение. Декартова прямоугольная система координат в пространстве называется правой (левой), если поворот от базисного вектора 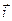 к вектору
к вектору 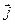 на наименьший угол виден с конца вектора
на наименьший угол виден с конца вектора 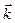 осуществляющимся против (по) часовой стрелки.
осуществляющимся против (по) часовой стрелки.
Говорят также, что тройка базисных векторов 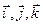 имеет правую (левую) ориентацию.
имеет правую (левую) ориентацию.
Определение. Векторным произведением двух неколлинеарных векторов 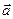 и
и 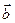 называется вектор
называется вектор 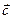 , перпендикулярный плоскости векторов
, перпендикулярный плоскости векторов 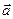 и
и 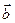 , имеющий длину, равную площади параллелограмма, построенного на векторах
, имеющий длину, равную площади параллелограмма, построенного на векторах 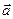 и
и 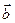 и направленный так, что тройка векторов
и направленный так, что тройка векторов 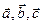 так же ориентирована, как и тройка базисных векторов
так же ориентирована, как и тройка базисных векторов 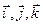 . Обозначение:
. Обозначение:  .
.
Векторное произведение двух коллинеарных векторов и в случае, когда один или оба сомножителя - нуль-векторы, по определению, равно нулю.
Теорема. Векторное произведение обладает следующими свойствами:
1)  2)
2)  3)
3) 
где 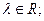
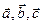 - произвольные векторы.
- произвольные векторы.
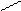 Докажем свойства 1) и 3). При
Докажем свойства 1) и 3). При 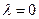 и при
и при  все части этих тождеств - нулевые векторы, т.е. тождества справедливы. Пусть
все части этих тождеств - нулевые векторы, т.е. тождества справедливы. Пусть  . Левая и правая части тождеств 1) и 3) определяют векторы, перпендикулярные одной и той же плоскости, т.е. коллинеарные друг другу. Длины этих векторов, как площади равных или равновеликих параллелограммов, равны. Эти векторы одинаково направлены. Действительно, поворот от вектора
. Левая и правая части тождеств 1) и 3) определяют векторы, перпендикулярные одной и той же плоскости, т.е. коллинеарные друг другу. Длины этих векторов, как площади равных или равновеликих параллелограммов, равны. Эти векторы одинаково направлены. Действительно, поворот от вектора 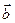 к вектору
к вектору 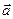 противоположен повороту от
противоположен повороту от 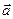 к
к 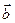 , а знак минус в тождестве 1) меняет направление вектора на противоположное. При
, а знак минус в тождестве 1) меняет направление вектора на противоположное. При  направления всех векторных произведений в тождестве 3) одинаковы, а при
направления всех векторных произведений в тождестве 3) одинаковы, а при 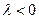 направление каждого векторного произведения этого тождества меняется на противоположное.
направление каждого векторного произведения этого тождества меняется на противоположное.
Пусть 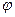 - угол между неколлинеарными векторами
- угол между неколлинеарными векторами 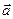 и
и 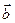
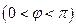 . Тогда
. Тогда

Теорема. Векторное произведение двух векторов
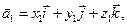
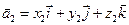 (4.1)
(4.1)
определяется формулой:

Доказательство. Из определения и свойств векторного произведения непосредственно следует, что правые части формул (4.1) можно перемножать как многочлен на многочлен, но, в отличие от скалярного произведения, со строгим соблюдением порядка следования множителей. Кроме того,

Получаем:
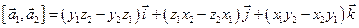 .
.
Правую часть этого равенства можно записать в виде определителя третьего порядка, в первой строке которого - базисные векторы 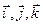 во второй - координаты первого вектора, в третьей - второго.
во второй - координаты первого вектора, в третьей - второго.
Следствие. Площадь треугольника с вершинами 
 равна половине модуля векторного произведения
равна половине модуля векторного произведения  , т.е.
, т.е.
 .
.
Векторное произведение является внутренней операцией умножения на множестве  векторов в пространстве. Эта операция антикоммутативна. Оказывается, что для векторного умножения не выполняется также закон ассоциативности, так как
векторов в пространстве. Эта операция антикоммутативна. Оказывается, что для векторного умножения не выполняется также закон ассоциативности, так как


т.е.
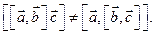
Пример. Найти векторное произведение векторов
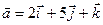 и
и  .
.
Имеем 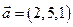 ;
; 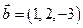 ;
;
 .
.
Пример. Вычислить площадь треугольника с вершинами 

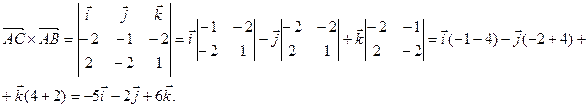

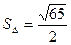 (ед2).
(ед2).
Пример. Доказать, что векторы 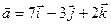 ,
, 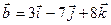 и
и  компланарны. Имеем:
компланарны. Имеем:
 . Векторы линейно зависимы, следовательно, они компланарны.
. Векторы линейно зависимы, следовательно, они компланарны.
Пример. Найти площадь параллелограмма, построенного на векторах 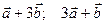 , если
, если 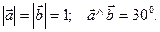
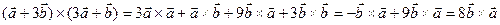
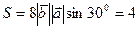 (ед2).
(ед2).
Дата добавления: 2015-11-28; просмотров: 836;
