Условие неразрывности струи

Рис.3

Для установления связи между скоростью ламинарного течения жидкости и площадью поперечного сечения участка, через который она протекает, выделим в трубке тока участки с площадью поперечного сечения S₁и S₂ (см.рис.3). В пределах этих сечений скорости частиц жидкости одинаковы, направлены перпендикулярно выделенным площадкам и равны по величине v₁ и v₂ соответственно. Объемы жидкости V₁ и V₂, протекающей через выделенное сечение за одно то же время t, одинаковы, так как жидкость практически несжимаема. Это позволяет записать равенство:

S₁v₁t = S₂v₂t или S₁v₁= S₂ v₂или Sv= const. (1)

Уравнение (1) представляет собой условие неразрывности струи, утверждающее, что при ламинарном течении жидкости произведение площади сечения участка, через который она протекает, на ее скорость является постоянной величиной для данной трубки тока.

При течении жидкости различают её линейную и объемную скорость. Линейная скорость (v) - это путь (L), проходимый частицами жидкости в единицу времени: v= L / t - для равномерного течения. Объемная скорость (или расход) (Q) - это объем жидкости (V), протекающий через некоторое сечение за единицу времени (t): Q = V / t.Объемная и линейная скорости течения жидкости связаны очевидным соотношением: Q = vS , где S - площадь поперечного сечения потока жидкости. Линейная скорость кровотока измеряется в м/с, а объемная - м³/с, л/мин, мл/мин и др.

Условие неразрывности струи (1) выполняется и в реальной гемодинамике. Здесь формулировка этого условия звучит следующим образом: в любом сечении сердечно-сосудистой системы объемная скорость кровотока одинакова:
Q = const.

Под площадью сечения сосудистой системы понимают суммарную площадь сечения кровеносных сосудов одного уровня ветвления. Так, в большом круге кровообращения первое (наименьшее по площади) сечение проходит через аорту, второе - через все артерии, на которые непосредственно разветвляется аорта, и т.д. Наибольшую площадь имеет сечение, соответствующее капиллярной сети.

Как следует из условия неразрывности струи, с увеличением площади сечения сосудистой системы скорость кровотока в ее соответствующих участках уменьшается. Так, в покое средняя линейная скорость кровотока в аорте составляет около 0,4-0,5 м/с, а в капиллярах - около 0,5 мм/с. Следовательно, сумма поперечных сечений всех функционирующих капилляров примерно в 800 раз больше площади сечения аорты.

Уравнение Бернулли

Основным количественным соотношением, описывающим течение идеальной (то есть абсолютно несжимаемой и невязкой) жидкости является уравнение Бернулли, вытекающее из закона сохранения энергии в движущейся жидкости.

Рис.4

Для его установления рассмотрим трубку тока идеальной жидкости, в которой выделим два сечения площадью S₁ и S₂ (рис.4). Пусть центры этих сечений расположены на высотах h₁ и h₂, отсчитываемых от некоторого уровня. Линейные скорости частиц жидкости в этих сечениях обозначим v₁ и v₂. Силы, обуславливающие течение жидкости, оказывают давление Р₁ и Р₂ на торцах объема жидкости между выделяемыми сечениями S₁ и S₂. При стационарном течении идеальной жидкости ее полная энергия в местах расположения выделенных сечений сохраняется, следовательно:

mv₁²/ 2 + Р₁V + mgh₁ = mv₂² / 2 + P₂V + mgh₂. (2)

В уравнении (2) m - одинаковая масса жидкости объема V, протекающей через сечения S₁ и S₂. Первые слагаемые в обоих частях равенства представляют кинетическую энергию жидкости, вторые - потенциальную энергию давления, третьи - потенциальную энергию, обусловленную расположением жидкости на высотах
h₁ и h₂.

Разделив правую и левую часть соотношения (2) на объем жидкости V и , вводя плотность жидкости r, получим:

rv₁²/2+P₁+rgh₁ = rv₂²/2+P₂+rgh₂ или rv²/2+P+rgh = const. (3)

Формула (3) называется уравнением Бернулли, утверждающим, что сумма разнопричинных давлений в жидкости (полное давление) является постоянной величиной. Слагаемое rv²/2 представляет динамическое давление, обусловленное движением жидкости; Р - статическое давление, не связанное с движением жидкости (оно может быть измерено, например, манометром, движущимся вместе с жидкостью); rgh - весовое (гидростатическое) давление.

Рассмотрим некоторые следствия, вытекающие из уравнения Бернулли:

а) Способ измерения скорости движения жидкости.

Рис.5

Представим, что в движущуюся жидкость опущены две трубки малого сечения, причем, плоскость поперечного сечения одной из них параллельна направлению скорости движения жидкости v, а другая (трубка Пито) изогнута так, что плоскость сечения изогнутой части перпендикулярна направлению скорости течения (рис.5). Подъем жидкости в прямой трубке на высоту h₁ обусловлен лишь статическим давлением Р_c, которое можно определить по формуле:
P_c= rgh₁. В трубке Пито подъем жидкости на высоту h₂ обусловлен полным давлением Р_п - в данном случае суммой статического Р_с и динамического Р_д давлений (течение происходит горизонтально и весовое давление не учитывается). Следовательно:

Р_п = Р_с + Р_д ; rgh₂ = rgh₁+ r v²/2 (4)

Из формулы (4) находим линейную скорость жидкости:

v = 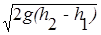. (5)

Таким образом, по измеренной разности уровней жидкости в прямой и изогнутой трубках определяется скорость течения жидкости.

б) Всасывающее действие струи.

Рассмотрим течение жидкости по горизонтальной трубе переменного сечения. Выделим два участка с площадью поперечного сечения S₁ и S₂, причем, для определенности, S₁> S₂ (рис.6). Запишем для данного случая уравнение Бернулли:

rv₁²/ 2 + P₁ = rv₂²/2 + P₂, (6)

Рис.6

где v₁и v₂ – скорости течения жидкости в сечениях S₁ и S₂. Статические давления Р₁ и Р₂ в соответствующих сечениях могут быть определены по высотам подъема жидкости
h₁ и h₂ в капиллярных трубках. Поскольку S₁> S₂, то v₁<v₂, - в узких местах жидкость течет быстрее. Тогда из уравнения (6) следует, что Р₁ > Р₂, т.е. статическое давление в более широкой части трубки большее, чем в ее узкой части. Если сужение значительно, то скорость жидкости в нем v₂намного превышает v₁, статическое давление Р₂ резко уменьшается и может стать ниже атмосферного. В этом случае воздух (или окружающая трубку другая среда) будет засасываться через отверстие в месте расположения сужения. На этом принципе устроены водоструйные насосы, ингаляторы, пульверизаторы и др.

<14 15 161718 19 20 >

Дата добавления: 2016-01-20; просмотров: 5794;