ОДНОКРАТНАЯ ПОПЕРЕЧНАЯ НЕСИММЕТРИЯ

Поперечная несимметрия в произвольной точке трехфазной системы в общем виде может быть представлена присоединением в этой точке трех неодинаковых сопротивлений. Такой подход позволяет получить решение в общем виде, из которого затем вытекают решения для всех частных случаев. Но такой подход приводит к громоздким выражениям, поэтому считается значительно проще и нагляднее проводить решение для каждого частного случая, используя характеризующие его граничные условия.

В этом разделе рассмотрены три основных вида несимметричных ко­ротких замыканий (двухфазное, однофазное на землю и двухфазное на зем­лю), наиболее часто случающиеся в системах с заземленной нейтралью. В приводимых ниже выкладках предполагается, что рассматриваются только основные гармоники тока и напряжения, причем схемы отдельных последовательностей состоят только из реактивных сопротивлений, найдены ре­зультирующая ЭДС 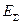и результирующие реактивности .

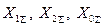При записи граничных условий примем, что фаза «А» находится в усло­виях, отличных от условий для двух остальных фаз, т.е. она является, как говорят, особой фазой. За положительное направление токов будем считать направление к месту короткого замыкания.

Для упрощения записи индекс вида короткого замыкания сохранен только при записи граничных условий и в окончательных результатах.

Приняв за особую фазу «А», можно составить уравнения ЭДС и напряжений контура для соответствующих последовательностей:

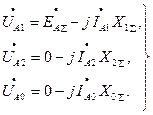(7.1)

Фазные токи и напряжения в месте короткого замыкания можно найти по формулам, полученным на основании (6.2)

(7.2)

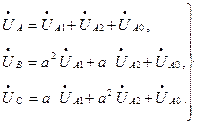(7.3)

В девяти уравнениях (7.1–7.3) имеется 12 неизвестных ( 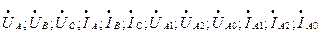). Чтобы решить эту систему уравнений, необходимо составить еще три уравнения, вытекающие из граничных условий соответствующего вида несимметричного короткого замыкания.