Значения усредненных коэффициентов местных сопротивлений (квадратичная зона)
| Сопротивление | ζкв | Сопротивление | ζкв |
| Вход в трубу: с острыми кромками вдающийся внутрь резервуара Выход из трубы Угольник с углом поворота: 45О 90О Колено плавное (90О) Тройник Шаровой кран Вентиль обычный Прижимная коробка трубы с клапаном и сеткой при dтр, мм: | 0,5 1,00 1,00 0,44 1,32 0,23 0,32 45,00 4,00 7,00 6,00 5,20 3,70 | Задвижка: полностью открытая (n=1) n=0,75 n=0,5 n=0,4 n=0,3 n=0,2 Кран пробковый Фильтры для нефтепродуктов: светлых темных Диафрагма с острыми кромками при n= Sот/Sтр: 0,4 0,5 0,6 0,7 | 0,15 0,20 2,00 4,60 10,00 35,00 0,40 1,70 1,20 7,00 4,00 2,00 0,97 |
Приложение 3.
Поправочная функция j для zкв в формуле z= jzкв
при ламинарном и переходном режимах движения
| Re | j | Re | j |
| 4,20 3,81 3,51 3,37 3,22 3,12 3,01 | 2,95 2,90 2,84 2,48 2,26 2,12 1,98 |
Приложение 4.
Теплофизические свойства некоторых жидкостей
| Свойство | Температура, оС | ||||||||
| Вода | |||||||||
| Плотность r, кг/м3 Динамическая вязкость h, мПа×с Давление насыщенных паров pп, кПа | 1,31 1,22 | 1,00 2,34 | 0,80 4,24 | 0,66 7,38 | 0,55 12,34 | 0,47 19,92 | 0,41 31,17 | 0,36 47,37 | 0,32 70,13 |
| Топливо Т-1 | |||||||||
| Плотность r, кг/м3 Динамическая вязкость h, мПа×с Давление насыщенных паров pп, кПа | –– –– –– | 1,49 4,67 | –– 7,47 | 1,08 11,21 | –– 15,61 | 0,83 21,35 | –– 28,02 | 0,66 36,02 | –– 44,43 |
| Масло МС-20 | |||||||||
| Плотность r, кг/м3 Динамическая вязкость h, мПа×с | 248,0 | 102,0 | 47,5 | 24,0 | 13,4 | 8,0 | 5,1 | 3,5 | 2,4 |
II. Задания для выполнения контрольных работ студентами – заочниками
Вариант 1
Номера контрольных задач выбираются согласно последней цифре шифра зачетной книжки студента (см. табл. 1.1), числовые значения указанных в задаче величин – по предпоследней цифре шифра зачетной книжки студента (табл. 1.2).
Таблица 1.1.
Номера задач для контрольных работ
| Последняя цифра шифра | При выполнении одной контрольной работы | |||||
| I вар. | II вар. | |||||
Задачи
1. Определить величину и направление силы F, приложенной к штоку поршня для удержания его на месте. Справа от поршня находится воздух, слева от поршня и в резервуаре, куда опущен открытый конец трубы, – жидкость Ж (рис. 1.1).
Показание пружинного манометра – PM.
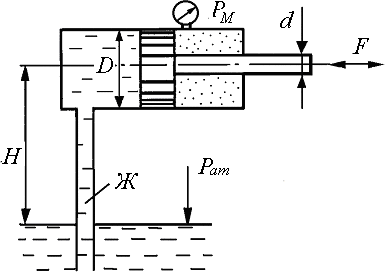
Рис. 1.1.
2. Паровой прямодействующий насос подает жидкость Ж на высоту Н (рис. 1.2). Каково абсолютное давление пара, если диаметр парового цилиндра D, а насосного цилиндра d? Потерями на трение пренебречь.
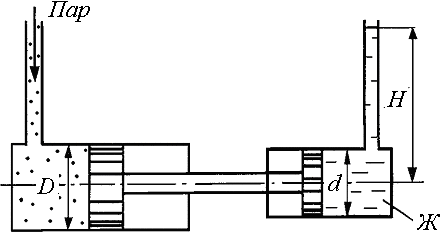
Рис. 1.2.
3. Определить силу прессования F, развиваемую гидравлическим прессом, у которого диаметр большего плунжера D, диаметр меньшего
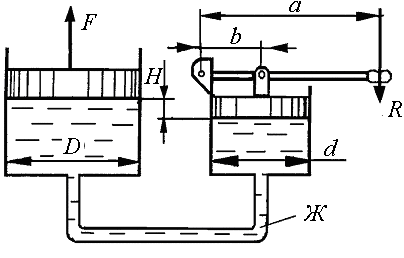
Рис. 1.3.
плунжера d. Больший плунжер расположен выше меньшего на величину Н, рабочая жидкость Ж, усилие, приложенное к рукоятке, R
(рис. 1.3).
4. Замкнутый резервуар разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а, закрытое крышкой (рис. 1.4). Давление над жидкостью Ж в левой части резервуара определяется показаниями манометра PM, давление воздуха в правой части – показаниями мановакуумметра. Определить величину и точку приложения результирующей силы давления на крышку.
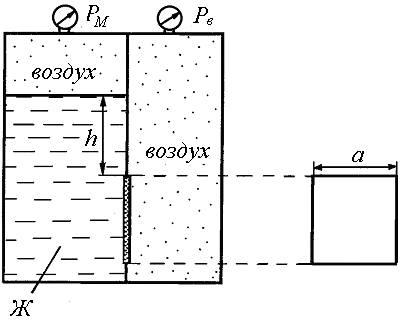
Рис. 1.4.
5. Шар диаметром D наполнен жидкостью Ж. Уровень жидкости в пьезометре, присоединенном к шару, установился на высоте Н от оси шара. Определить силу давления на боковую половину внутренней поверхности шара (рис. 1.5). Показать на чертеже вертикальную и горизонтальную составляющие, а также полную силу давления.
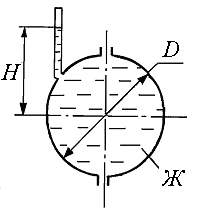
Рис. 1.5.
6. Определить силу давления на коническую крышку горизонтального цилиндрического сосуда диаметром D, заполненного жидкостью Ж
(рис. 1.6). Показание манометра в точке его присоединения – PM. Показать на чертеже вертикальную и горизонтальную составляющие, а также полную силу давления.
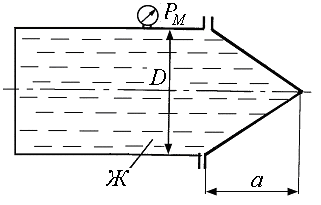
Рис. 1.6.
7. При истечении жидкости из резервуара в атмосферу по горизонтальной трубе диаметра d и длиной 2l уровень в пьезометре, установленном посередине длины трубы, равен h (рис. 1.7). Определить расход Q и коэффициент гидравлического трения трубы l, если статический напор в баке постоянен и равен Н. Построить пьезометрическую и напорную линии. Сопротивлением входа в трубу пренебречь.
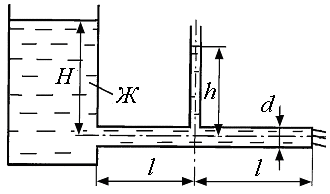
Рис. 1.7.
8. Жидкость Ж подается в открытый верхний бак по вертикальной трубе длиной l и диаметром d за счет давления воздуха в нижнем замкнутом резервуаре (рис. 1.8). Определить давление P воздуха, при котором расход будет равен Q. Принять коэффициенты сопротивления вентиля xв = 8,0; входа в трубу xвх = 0,5; выхода в бак xвых = 1,0. Эквивалентная шероховатость стенок трубы kЭ = 0,2 мм.
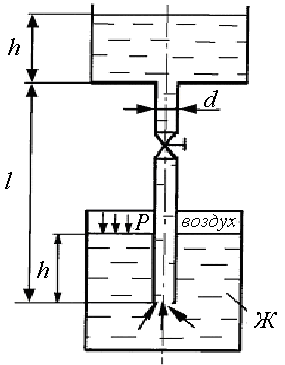
Рис. 1.8.
9. Поршень диаметром D движется равномерно вниз в цилиндре, подавая жидкость Ж в открытый резервуар с постоянным уровнем (рис. 1.9). Диаметр трубопровода d, его длина l. Когда поршень находится ниже уровня жидкости в резервуаре на Н = 0,5 м, потребная для его перемещения сила равна F. Определить скорость поршня и расход жидкости в трубопроводе. Построить напорную и пьезометрическую линии для трубопровода. Коэффициент гидравлического трения трубы принять l = 0,03. Коэффициент сопротивления входа в трубу xвх = 0,5. Коэффициент сопротивления выхода в резервуар xвых = 1,0.
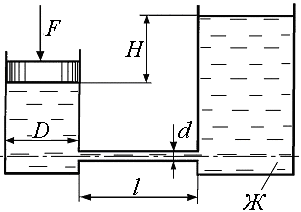
Рис. 1.9.
10. Определить диаметр трубопровода, по которому подается жидкость Ж с расходом Q из условия получения в нем максимально возможной скорости при сохранении ламинарного режима. Температура жидкости t = 20 °С.
11. При ламинарном режиме движения жидкости по горизонтальному трубопроводу диаметром d = 30 см расход равнялся Q, а падение пьезометрической высоты на участке данной l составило Н. Определить кинематический и динамический коэффициенты вязкости перекачиваемой жидкости.
12. По трубопроводу диаметром d и длиной l движется жидкость Ж
(рис. 1.10). Чему равен напор Н, при котором происходит смена ламинарного режима турбулентным? Местные потери напора не учитывать. Температура жидкости t = 20 °С.
У к а з а н и е. Воспользоваться формулой для потерь на трение при ламинарном режиме (формула Пуазейля).
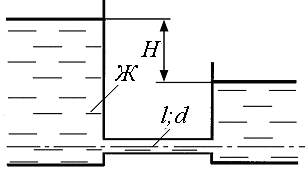
Рис. 1.10.
13. На поршень диаметром D действует сила F (рис. 1.11). Определить скорость движения поршня, если в цилиндре находится вода, диаметр отверстия в поршне d, толщина поршня а. Силой трения поршня о цилиндр пренебречь, давление жидкости на верхнюю плоскость поршня не учитывать.
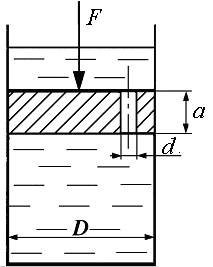
Рис. 1.11.
14. Определить длину трубы l, при которой расход жидкости из бака будет в два раза меньше, чем через отверстие того же диаметра d. Напор над отверстием равен Н. Коэффициент гидравлического трения в трубе принять l = 0,025 (рис. 1.12).
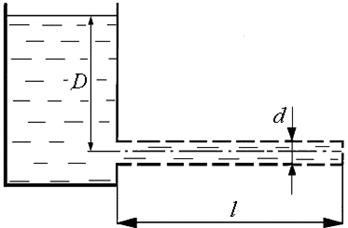
Рис. 1.12.
15. Определить длину трубы l, при которой опорожнение цилиндрического бака диаметром D на глубину Н будет происходить в два раза медленнее, чем через отверстие того же диаметра d. Коэффициент гидравлического трения в трубе принять l = 0,025 (рис. 1.12).
У к а з а н и е. В формуле для определения времени опорожнения бака коэффициент расхода m выпускного устройства определяется его конструкцией. Для трубы
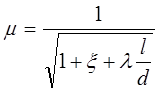 ,
,
где x - суммарный коэффициент местных сопротивлений.
16. Определить диаметр d горизонтального стального трубопровода длиной l = 20 м, необходимый для пропуска по нему воды в количестве Q, если располагаемый напор равен Н. Эквивалентная шероховатость стенок трубы k = 0,15 мм.
У к а з а н и е. Для ряда значений d и заданного Q определяется ряд значений потребного напора HП. Затем строится график НП = f(d) и по заданному Н определяется d.
17. Из бака А, в котором поддерживается постоянный уровень, вода протекает по цилиндрическому насадку диаметром d в бак В, из которого сливается в атмосферу по короткой трубе диаметром D, снабженной краном (рис. 1.13). Определить наибольшее значение коэффициента сопротивления крана x, при котором истечение из насадка будет осуществляться в атмосферу. Потери на трение в трубе не учитывать.
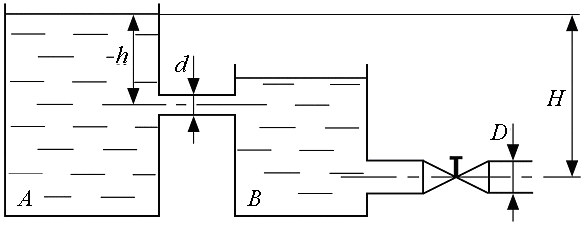
Рис. 1.13.
18. При внезапном расширении трубопровода скорость жидкости в трубе большего диаметра равна v. Отношение диаметров труб D/d = 2
(рис. 1.14). Определить Н – разность показаний пьезометров.
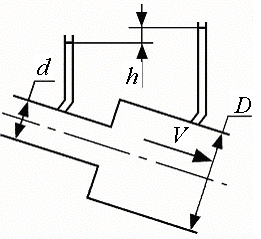
Рис. 1.14.
19. Горизонтальная труба служит для отвода жидкости Ж в количестве Q из большого открытого бака (рис. 1.15). Свободный конец трубы снабжен краном.
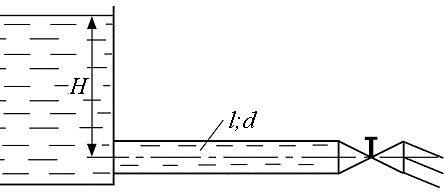
Рис. 1.15.
Определить ударное повышение давления в трубе перед краном, если диаметр трубы d, длина l, толщина стенки d, материал стенки - сталь. Кран закрывается за время tзак по закону, обеспечивающему линейное уменьшение скорости жидкости в трубе перед краном в функции времени.
20. Вода в количестве Q перекачивается по чугунной трубе диаметром d, длиной l с толщиной стенки d. Свободный конец трубы снабжен затвором. Определить время закрытия затвора при условии, чтобы повышение давления в трубе вследствие гидравлического удара не превышало DP = 1 МПа. Как повысится давление при мгновенном закрытии затвора?
21. Определить время закрытия задвижки, установленной на свободном конце стального водопровода диаметром d, длиной l с толщиной стенки d, при условии, чтобы максимальное повышение давления в водопроводе было в три раза меньше, чем при мгновенном закрытии задвижки. Через сколько времени после мгновенного закрытия задвижки повышение давления распространится до сечения, находящегося на расстоянии 0,7  l от задвижки?
l от задвижки?
Приложения к задачам варианта 1
Таблица 1.3.
1. Удельный вес g и плотность r жидкостей при t = 20° C.
| Наименование | g, Н/м3 | r, кг/м3 |
| Бензин авиационный | 7250÷350 | 739÷751 |
| Вода пресная | 998,2 | |
| Глицерин безводный | ||
| Керосин | 7770÷8450 | 792÷840 |
| Масло касторовое | ||
| Масло минеральное | 8600÷8750 | 877÷892 |
| Нефть | 8340÷9320 | 850÷950 |
| Ртуть | ||
| Спирт этиловый безводный | 789,3 | |
| Масло трансформаторное | 8870÷8960 | 904÷915 |
| Масло турбинное | 9200÷9300 | 940÷952 |
Таблица 1.4.
2. Кинематический коэффициент вязкости жидкостей n при t = 20° C.
| Жидкость | n, см2/с | Жидкость | n, см2/с | |
| Бензин авиационный | 0,0073 | Глицерин | 8,7 | |
| Керосин Т-1 | 0,025 | Воздух | 0,149 | |
| Вода | 0,010 | Масло трансформаторное | 0,3 | |
| Ртуть | 0,0016 | |||
| Масло индустриальное (веретенное) | 0,5 |
Таблица 1.5
3. Давление насыщения паров, МПа (абс.)
| Вещество | Температура, °С | ||||
| Бензин Б-70 | 0,0163 | 0,0332 | 0,056 | 0,1 | - |
| Керосин Т-1 | 0,0035 | 0,0058 | 0,0075 | 0,0012 | 0,02 |
| Вода | 0,0033 | 0,008 | 0,02 | 0,048 | 0,1 |
| Спирт | 0,008 | 0,02 | 0,049 | - | - |
Таблица 1.6.
4. Модуль упругости жидкостей при t = 50° C, МПа
| Жидкость | Модуль упругости | Жидкость | Модуль упругости |
| Вода | Турбинное масло | ||
| Спирт | |||
| Нефть | Глицерин | ||
| Керосин | |||
| Ртуть |
5. Модуль упругости металлов, МПа
Сталь ………………………………. 2×105
Чугун ………………………………. 105
Вариант 2
Номера контрольных задач студент выбирает по последней цифре шифра зачетной книжки студента (табл. 2.1), а числовые значения – по предпоследней цифре (табл. 2.2).
В условиях контрольных работ не всегда указывают все цифровые значения параметров, необходимых для решения задач (например, может быть не указана плотность, коэффициент вязкости или другой параметр). Тогда недостающие параметры выбираются из таблиц, помещенных в приложении. В исключительных случаях можно пользоваться также данными других справочников, в каждом случае указывая в своей контрольной работе название справочника, номер таблицы или графика.
Таблица 2.1.
Дата добавления: 2016-01-20; просмотров: 2611;
