Процесс непрерывного дозирования

Непрерывное дозирование – сложный технологический процесс, обеспечивающий требуемую производительность – массовый расход сыпучих материалов и жидкостей.

Объект регулирования в этом ТП – дозатор (Рис. 16.8).

Автоматическое непрерывное весовое дозирование материала производится бункерными и ленточными дозаторами. Для обоих типов весовых дозаторов

.

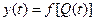Для бункерного дозатора основной параметр - расход материала

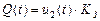. (16.1)

где Q(t) - изменение массы материала в бункере; 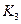- коэффициент передачи задвижки, кг / {с [и₂(t)]}. Здесь [и₂(t)] означает размерность управляющего воздействия и₂ (t).

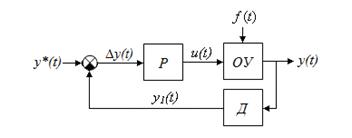
Рис. 16.7 – Структурная схема САР непрерывного ТП: Р - регулятор; ОУ - объект управления; Д - датчик выходного параметра; y*(t) - заданный параметр; ∆y(t) - рассогласование; u(t) – управляющее воздействие; y(t) - регулируемый параметр; y1(t) - измеренное значение параметра; f(t) - возмущающее воздействие

В операторной форме .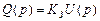

Передаточная функция бункерного дозатора

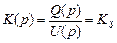. (16.2)

Выражения (16.1), (16.2) справедливы в пределах времени Т_ц, когда масса материала М₀ в бункере не равна нулю.

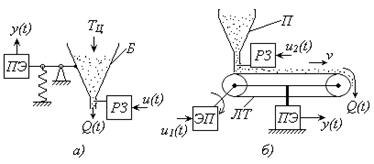
Рис. 16.8 – Процессы непрерывного дозирования: а) бункерный весовой дозатор; б) ленточный весовой дозатор; Б – бункер; ТЦ – цикл загрузки бункера; ПЭ - преобразующий элемент; РЗ – регулирующая задвижка; Q(t) – расход материала (кг/с); П – питатель; ЛТ – ленточный транспортер; ЭП – ленточный электропривод транспортера; v – скорость движения ленты транспортера; y(t) – выходной параметр; u(t), u1(t), u2(t) – управляющие воздействия

Для ленточного весового дозатора, очевидно, что при постоянной скорости движения ленты (v=const) расход материала 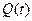будет также определяться величиной открытия задвижки ( 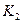). В этом случае также будут справедливы соотношения (16.1), (16.2) при К_З = К₂. При изменении скорости ленты v, величина 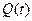тоже будет изменяться. При этом

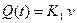, (16.3)

где 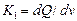- постоянная величина, определяемая техническими параметрами электропривода ЭП.

Скорость ленты зависит от входного воздействия 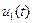, управляющего электроприводом, для которого

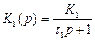. (16.4)

Кроме этого будет иметь место запаздывание t₃, обусловленное конечной скоростью движения ленты и ее длиной L:

.

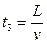В операторной форме это явление учитывается запаздывающим звеном, для которого

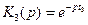. (16.5)

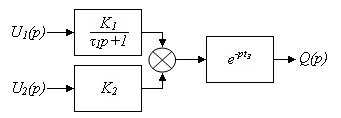
Учитывая формулы (16.3), (16.4) и (16.5) можно построить структурную схему ленточного дозатора (Рис. 16.9), соответствующую его функциональной схеме, приведенной на рис. 16.8,б).

Рис. 16.9 – Структурная схема ленточного весового дозатора