Общие сведения о нелинейных элементах и цепях

Нелинейным элементом (НЭ) называется элемент электрической цепи, параметры которого зависят от значений токов и напряжений.

Нелинейная цепь – это цепь, содержащая хотя бы один нелинейный элемент.

Параметры элементов линейных цепей – R, L и C не зависят от электрических величин – тока и напряжения. Однако на практике большинство электротехнических устройств содержат элементы, параметры которых в большей или меньшей степени зависят от токов и напряжений в этих элементах, то есть R(i) или R(u), L(i) и C(u) (Рис. 2.19). Если в линейных элементах ток и напряжение связаны линейными зависимостями:

, , ,

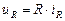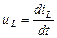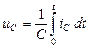то для НЭ эти соотношения не будут выполняться.

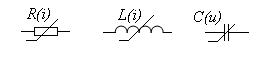
Рис. 2.19 – Нелинейные элементы

Свойства НЭ могут быть определены из их характеристик: вольтамперной i_R = f(u_R) для нелинейного активного сопротивления, вебер-амперной Ψ_L = f(i_L) для нелинейной индуктивности и кулон-вольтной q_C = f(u_C) для нелинейной емкости.

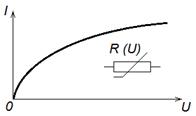
Пример вольтамперной характеристики (ВАХ) нелинейного активного сопротивления приведен на Рис. 2.20.

Рис. 2.20 – ВАХ нелинейного элемента

Нелинейные элементы могут быть управляемыми и неуправляемыми. Неуправляемый нелинейный элемент описывается одной характеристикой. Примерами таких элементов являются: терморезистор, катушка индуктивности с ферромагнитным сердечником, полупроводниковый диод, лампа накаливания. Управляемые нелинейные элементы, у которых характеристики зависят от управляющего фактора, описываются семейством характеристик. Такими элементами являются: транзистор, тиристор, операционный усилитель (как элемент цепи).

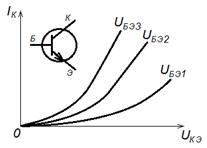
Пример семейства ВАХ транзистора приведен на Рис. 2.21.

По определению, электрическая цепь является нелинейной, если она содержит хотя бы один нелинейный элемент. Процессы в нелинейных элементах и в нелинейных цепях описываются нелинейными алгебраическими и дифференциальными уравнениями. Для нелинейных цепей неприменимы методы расчета, основанные на принципе суперпозиции: метод наложения, метод контурных токов, метод эквивалентного генератора.

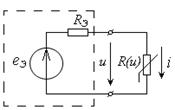
Рассмотрим цепь с нелинейным резистивным элементом, находящуюся под воздействием переменной ЭДС (Рис. 2.22).

Рис. 2.22 – цепь с нелинейным резистивным элементом
Рис. 2.21 – Семейство ВАХ транзистора IK = f(UKЭ) при различных значениях UБЭ

Пусть переменная ЭДС будет задана в виде гармонического колебания

е_Э = E_m sin (ωt – Ψ₁), . (2.42)

где E_m – амплитуда, ω – круговая частота, Ψ₁ = ωt₁ – начальная фаза.

С учетом этого формулу (2.42) получим в виде

е_Э = E_m sin ω(t – t₁).

Ток i через НЭ будет выражаться соотношением:

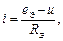(2.43)

которое называют нагрузочной характеристикой.

Графически нагрузочная характеристика будет представлять собой прямую линию, проходящую через точки u = е_Э = E_m sin ω(t – t₁) на оси абсцисс и точки е_Э / R на оси ординат.

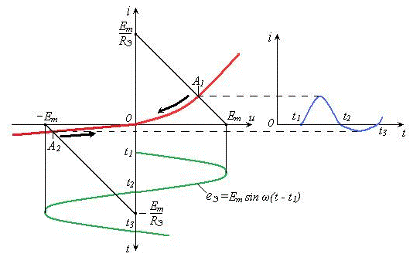
На рис. 2.23 показаны крайние положения нагрузочной характеристики, когда е_Э = ± E_m и ток i = ± E_m/R. Положение нагрузочной характеристики будет зависеть от времени t, определяющего точку ее пересечения с осью абсцисс. С течением времени эта точка будет перемещаться по ВАХ нелинейного элемента из положения А₁ в положение А₂ и обратно.

Рис. 2.23 – Графики, поясняющие процессы в нелинейной цепи

Каждому положению рабочей точки на ВАХ будет соответствовать определенное значение тока i через нелинейный элемент (Рис. 2.23). Форма тока отличается от формы переменной ЭДС, действующей в цепи. Это отличие обусловлено нелинейностью ВАХ элемента R(u), параметр которого (активное сопротивление) зависит от напряжения u. Ток i не является гармоническим, то есть колебанием одной частоты. Он будет являться периодическим несинусоидальным колебанием с периодом Т = 2π/ω. Частотный спектр такого тока будет содержать гармонические колебания с частотами, кратными частоте переменной ЭДС.

Свойства нелинейных элементов используются при различных преобразованиях электрических колебаний, таких как: выпрямление переменного тока, генерирование и усиление, преобразование формы колебаний, регистрация и измерение неэлектрических величин и так далее.