Эпюры внутренних сил.

Внутренние усилия изменяются по длине стержня. Исследование соответствующих зависимостей удобно осуществлять с помощью графиков, так называемых эпюр внутренних усилий. Рассмотрим несколько примеров.

Пример 2.1.1 Пусть имеем расчетную схему прямого стержня АВС. К стержню приложены три внешние сосредоточенные силы F_A= 8 кН, F_B = 14 кН, F_C = 6 кН, рис. 2.1.7, а. Силы действуют по оси стержня и удовлетворяют условиям равновесия. Определить внутренние усилия и построить соответствующую эпюру.

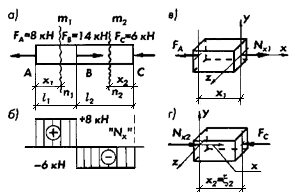
Рисунок 2.1.7

Сечением В, в котором приложена сила F_B, весь стержень подразделяется на два участка длиной l₁ и l₂‚, рис. 2.1.7, а. В пределах первого из них имеем внутреннюю нормальную силу N_x1 =+ F_A = +8 кH, в пределах второго — нормальную силу N_x2 = F_C = -б кН, см эпюру N_x (х) на рас, 2.1.7, б. Чтобы удостовериться в справедливости сказанного, займемся вопросом подробнее.

Проведем в пределах первого участка произвольное сечение m₁n₁ и обозначим расстояние до него от левого конца через х₁ рис. 2.1.7, а. На рис. 2.1.7, в изображена левая отсеченная часть стержня. Чтобы соблюдалось условие равновесия ∑F= 0, к этому телу в сечении m₁n₁ нужно приложить силу N_x1 так, как показано на рис. 2.1.7, в. Из этого условия получаем модуль внутреннего усилия 1N_x11 = 1F_A1 = 8 кН. В соответствии с правилом знаков, данным выше, приходится этому усилию приписать положительный знак. Можно убедиться самостоятельно в том, что а условий равновесия правой отсеченной части даст тот же ответ как по модулю, так и по знаку (с учетом при правила знаков). Добавим, что в пределах первого участка: усилие N_x1 не зависит от координаты х₁ усилия Q_x , Q_y, М_х, M_y и М_z отсутствуют; это означает, что пять из шести уравнений обращаются в тождества вида 0=0.

Система сил F_A и N_x1 приложенных к левой отсеченной части стержня, вызывает ее растяжение. Можно показать, что положительные внутренние нормальные усилия всегда сопровождаются растяжением соответствующей части стержня, если придерживаться принятого выше правила знаков для внутренних сил.

Проведем произвольное сечение m₂n₂ в пределах второго участка стержня. Обозначим через х₂ расстояние от правого конца до сечения и изобразим правую отсеченную часть стержня, рис. 2.1.7, г. Из условия равновесия имеем 1N_x21 = 1F_с1 = б кН. Так как - сила N_x2 направлена в положительном направлении внутренней нормали х, то согласно принятому правилу знаков приходится принять N_x2= -6 кН. Система сил F_с и N_x2 сжимает отсеченную часть стержня. Более того, отрицательной нормальной силе всегда отвечает сжатие стержня.

Вызывает некоторое неудобство различие в направлениях оси х в сечениях m₂n₂ и координаты х Разрешением этого формального противоречия будет, скажем, введение обозначения ξ₂= х₂

Анализируя построенную на рис. 2.1.7, б эпюру N_x (х), отметим наличие скачков. Эти скачки отвечают сосредоточенным силам, причем численно значение скачка всегда равно модулю силы,

В заключение укажем, что на рис. 2.1.7 используется прием, упрощающий построение эпюры. В этом подвижная система координат xyz, связанная с произвольным сечением, поступательно перёмещается от одного конца стержня к другому последовательно через все участки.

В заключение сделаем несколько замечаний.

Во-первых, проекция изогнутой оси балки несколько короче начальной длины этой оси в прямой балке (до приложения внешних нагрузок). В элементарной теории изгиба балок этим обстоятельством обычно пренебрегают. Однако на практике с этим эффектом необходимо считаться. Например, при необходимости закрепления балки на двух и более опорах лишь одна из них может быть неподвижна в продольном направлении. В противном случае в такой балке возникают значительные продольные усилия, которые представляют опасность не столько самой балке, сколько ее опорам. Обязательность описанной нормы обуславливается также возможностью появления дополнительных продольных усилий за счет нагрева или охлаждения всей конструкции в целом.

Во-вторых, скачки на эпюрах внутренних усилий нужно рассматривать как результат идеализации внешних нагрузок («сосредоточенная» сила или «сосредоточенный момент»).

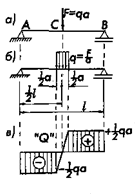
Рисунок 2.1.8

Предположим что сила F равномерно распределена с интенсивностью q на малом отрезке длиной а в ближайшей окрестности точки С, т. е. имеем F = qa. В этом случае эпюра поперечных сил принимает вид, изображенный на рис. 2.1.8, в. Таким образом, переход от идеальной схемы, к более реальной схеме устраняет неопределенность в определении значения поперечной силы в сечения С.

В-третьих, реальная конструкция, которой соответствует расчетная схема на рис. 2.1.8, а, обычно переходят в состояние разрушения следующим образом: возникает трещина в том поперечном сечении, где приложена сила F, здесь имеет место наибольший изгибающей момент. Следовательно, именно с изгибающим моментом следует связывать разрушение балок. В одной из последующих лекций будет показано, что иногда разрушение балки определяется не изгибающим моментом, а поперечной силой. Возможность разрушения тем или иным способом определяется в каждом конкретном случае численным расчетом. Поэтому в ходе такого расчета инженеру необходимо иметь одновременно как эпюру Q, так и эпюру М

Пример 1.2. На рис. 2.1.9, а изображена схема Г-образной рамы АВС. Рама заделала концом С, а на свободном конце А имеет вертикально приложенную силу F.

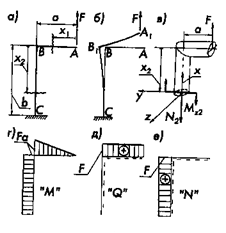
Рисунок 2.1.9

Найти реакции в опорном закреплении, определить внутренние усилия М, Q и N (с построением эпюр), изобразить примерный вид изогнутой оси рамы.

В глухой заделке, как установлено выше, могут возникнуть три реакции, рис. 2.1.9, а. Из уравнений равновесия

∑F_x=0 , ∑F_y=0, ∑m_2(C)=0

устанавливаем:

H_C=0 , R_C=F , M_C=Fa

Участок ВА данной рамы работает как консоль поэтому эпюры Q и М будут как показано на рисунке. Перейдем ко второму участку ВС. Проведем произвольное сечение на расстоянии х от верхнего конца В. На рис. 2.1.9, в изображена верхняя отсеченная часть рамы. С упомянутым произвольным сечением связана подвижная система координат хуz так, чтобы ось х сохранила направление одноименной оси из предыдущего участка, а ось х была направлена вдоль оси стержня. Направление оси х подчиняют обычно еще одному требованию: на обоих участках направления осей х согласуется с направлением обхода рамы, начиная с одного из ее концов, в данном случае — с конца С.

Из условий равновесия отсеченной части и с учетом правила знаков находим выражения для внутренних усилий:

M_z = F а , Q_y2= 0, N₂ = F

Соответствующие эпюры смотри на рис. 2.1.9, г, д и е. Эпюра М построена на сжатой стороне изогнутого второго участка рамы.

Примерный вид изогнутой оси рамы дается на рис. 2.1.9, 6. Обращаем внимание, что при этом построении учтено свойство глухой заделки С: она запрещает как вертикальное и горизонтальное перемещение соответствующего сечения стержня рамы, так и поворот этого сечения. Добавим, что при этом построении учтено требование приближенной теории изгиба стержней: длина первоначально прямого стержня и длина проекции искривленного стержня на начальное направление равны. В соответствии с этим правилом узел В, поворачиваясь и перемещаясь налево, не перемещается в вертикальном направлении.

В заключение укажем на вспомогательный прием, используемый при построении эпюр. Он заключается в том, что значками «—« отмечается на чертеже так называемая внутренняя сторона рамы на которой затем откладываются отрицательные ординаты соответствующих эпюр. При обходе рамы с одного конца до другого ее внутренняя сторона все время должна оставаться с одной и той же стороны.

Приведем некоторые правила построения эпюр (применительно к плоскости ху).

1. Каждая ордината эпюры Q, в любом сечении равна в некотором масштабе взятому с обратным знаком тангенсу образуемого с осью х угла наклона касательной к эпюре М_х.

2. При отсутствии на участке балки распределенной нагрузки, т. е. при q= 0 имеем Q = const и tgβ=0. Следовательно эпюра Q отражается отрезком прямой параллельной оси абсцисс

3. Если участок балки нагружен равномерно распределенной нагрузкой интенсивности q_у = const, то эпюра Q очерчивается наклонным отрезком прямой. Причем значения Q убывают (tgβ<0) при q_у > 0 (нагрузка направлена вверх) и возрастают при q_у <0 (tgβ>0).

4. При q_у > 0 Следовательно, эпюра моментов представляет собой вогнутую кривую, т. е. имеющую положительную кривизну. При q_у <0 эпюра М выпукла.

5. Если на некотором участке

— Q_у >0, то имеем tgа <0 и убывающую эпюру М;

— Q_у <0, то имеем tgа > 0 и возрастающую эпюру М;

— Q_у переходит через нуль, меняя знак, то эпюра М имеет экстремум;

— Q_у = 0, т. е tgа = 0, то получаем М = const;

б. Сосредоточенной силе, приложенной в некотором сечении, соответствует скачок на эпюре Q_у, а также резкое изменение угла наклона (излом) смежных участков эпюры М

7. В сечении, где приложена пара сил, эпюра М имеет скачок, равный моменту этой пары. На эпюре Q_у это не отражается.