Внешние и внутренние силы.

Внешними называют силы, действующие на тело со стороны точек или тел, не входящих в данное тело или систему. Внутренними называют силы, с которыми точки данного тела действуют друг на друга.

Разрушение или даже просто выход из строя конструкционного элемента возможны лишь при возрастании внутренних усилий и при переходе их через некоторый предельный барьер. Высоту этого барьера удобно отсчитать от того уровня, который отвечает отсутствию внешних сил. По существу нужно принять во внимание лишь дополнительные внутренние усилия, возникающие только при наличии внешних сил. Эти дополнительные внутренние силы называют в механике просто внутренними усилиями в узком, механическом смысле.

Определяются внутренние усилия с помощью «метода сечений», в основе которого лежит достаточно очевидное утверждение: если тело в целом находится в равновесии, то и любая выделен из него часть также находится в этом состоянии

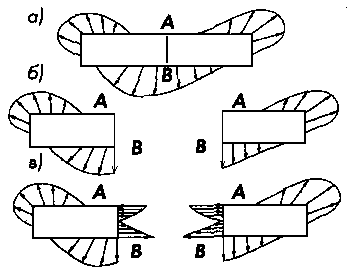
Рисунок 2.1.5

Рассмотрим стержень, находящийся в равновесии под действием системы внешних сил, рис. 2.1.5, а. Сечением АВ мысленно разделим его на две части, рис. 2.1.5, б. К каждому из сечений АВ левой и правой частей приложим систему усилий, соответствующую внутренним усилиям, действующим в реальном теле, рис. 1.7, в. Таким образом, с использованием метода сечений внутренние силы переводятся во внешние по отношению к каждой из отсеченных частей тела, что позволяет определять их из условий равновесия каждой из этих частей в отдельности.

Сечение АВ может быть ориентировало любым образом, но более удобным для дальнейших рассуждений оказывается поперечное сечение, перпендикулярное продольной оси стержня.

Введем обозначения:

, , ,

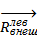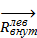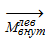
главные векторы и главные моменты внешних и внутренних сил, приложенных к левой отсеченной части. С учетом введенных обозначений условия равновесия этого тела можно записать в виде:

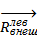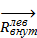+ =0, + =0 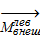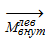(2.1.1)

Аналогичные выражения могут быть составлены и для правой отсеченной части стержня. После несложных преобразований можно получить:

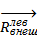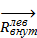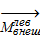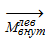=- , =- (2.1.1)

что может быть истолковано как следствие известного закона механики: действие всегда сопровождается равным и противоположно направленным противодействием.

В случае решения задачи о динамическом воздействии на стержень можно обратиться к известному принципу Даламбера, согласно которому к внешним силам присоединяются силы инерции, что вновь сводит задачу к уравнениям равновесия. Следовательно, процедура метода сечений остается

Величины и 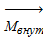не зависят от ориентации сечения АВ (см. рис. 2.1.5). Однако в практических расчетах наиболее удобным представляется использование поперечного сечения. В этом случае нормаль к сечению совпадает с продольной осью стержня. Далее главный вектор и главный момент внутренних сил обычно представляют в виде их проекций на ортогональные оси координат, причем одна из осей (например, ось х) совмещается с упомянутой нормалью см. рис. 2.1.6.

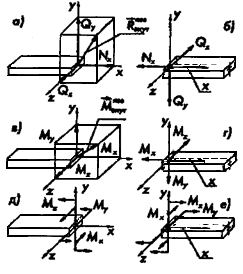
Рисунок 2.1.6

Разложим векторы 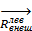, , 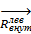, 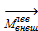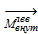по осям координат, рис. 2.1.6, а—г. Компоненты главного вектора и главного момента имеют общепринятые названия. Усилие N_x нормальное к плоскости сечения, называют нормальной (продольной) силой, а Q_x и Q_y— поперечными (перерезывающими) силами. Моменты относительно осей у и z, т. e. M_y и М_z будут изгибающими а момент относительно продольной оси х, т.е. М_х — крутящим.

Компоненты главного момента внутренних сил в сопротивлении материалов чаще всего отображают так, как дано на рис. 2.1.6, д и е.

Векторные уравнения равновесия могут быть представлены в виде проекции на оси координат:

Таким образом, каждый компонент главного вектора для главного момента внутренних сил подсчитывается как сумма проекций всех внешних сил на соответствующую ось или как сумма моментов всех внешних сил относительно этой оси (с учетом принятого правила знаков), расположенных по одну сторону от сечения.

Проекция вектора на ось координат, являясь величиной скалярной, может быть как положительной, так и отрицательной. Это зависит от того, совпадает направление проекции с положительным или отрицательным направлением оси соответственно. Для внутренних усилий это правило соблюдается лишь для случая, когда нормаль х является внешней, как это имело место для левой отсеченной части на рис. 2.1.6. В ситуации, когда нормаль х является внутренней, см. правую отсеченную часть на рис. 2.1.6, знак внутреннего усилия принимается положительным при совпадении его направления с отрицательным направлением оси. На рис. 2.1.6 все проекции внутренних усилий N_x, Q_x , Q_y, М_х, M_y и М_z (как относящиеся к левой, так и относящиеся к правой отсеченным частям) изображены положительными.