Минимизация функций. Запись функции в СДНФ не единственно возможная и, как правило, не самая короткая
Запись функции в СДНФ не единственно возможная и, как правило, не самая короткая. Чем меньше элементов содержит аналитическое выражение, тем проще логическая схема.
Выражение (1.1) можно упростить, если добавить в него дважды abc (закон тавтологии), сгруппировать попарно слагаемые (сочетательный закон) и исключить (закон склеивания) переменные, которые в группе меняют свои значения.
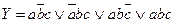
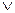 abc
abc 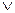 abc= (abc
abc= (abc 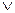 a
a 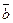 c)
c) 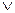 (abc
(abc 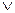
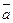 bc)
bc) 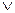 (abc
(abc 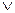 ab
ab 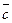 ) =
) =
= ac(b 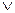
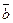 )
) 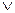 bc(a
bc(a 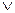
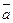 )
) 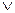 ac(c
ac(c 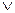
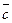 ) = ac
) = ac 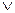 bc
bc 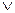 ac (1.2)
ac (1.2)

Рис. 1.7. Схема, реализующая (1.2).
a) в булевском базисе; б) в базисе И-НЕ.
В инженерной практике для минимизации наиболее часто применяют карты Карнау (Карно).
Карты Карно – это графическое представление таблиц истинности логических функций. Структура карт для функций двух, трех и четырех переменных показана ниже.
Таблица истинности (а) и структура карты Карно (б) для функции двух переменных.
| x1 | x2 | f(x1,x2) |
| f(0,0) | ||
| f(0,1) | ||
| f(1,0) | ||
| f(1,1) |
| x2 | |||
| x1 | |||
| f(0,0) | f(0,1) | ||
| f(1,0) | f(1,1) |
|
|
Таблица истинности (а) и cтруктура карты Карно (б) для функции трех переменных.
| x1 | x2 | x3 | f(x1,x2,x3) |
| f(0,0,0) | |||
| f(0,0,1) | |||
| f(0,1,0) | |||
| f(0,1,1) | |||
| f(1,0,0) | |||
| f(1,0,1) | |||
| f(1,1,0) | |||
| f(1,1,1) |
| а) |
| x2,x3 | ||||||
| x1 | ||||||
| f(0,0,0) | f(0,0,1) | f(0,1,1) | f(0,1,0) | |||
| f(1,0,1) | f(1,1,1) | f(1,1,0) |
Cтруктура карты Карно для функции четырех переменных.
| x3,х4 | |||||
| x1,х2 | |||||
| f(0,0,0,0) | f(0,0,0,1) | f(0,0,1,1) | f(0,0,1,0) | ||
| f(0,1,0,0) | f(0,1,0,1) | f(0,1,1,1) | f(0,1,1,0) | ||
| f(1,1,0,0) | f(1,1,0,1) | f(1,1,1,1) | f(1,1,1,0) | ||
| f(1,0,0,0) | f(1,0,0,1) | f(1,0,1,1) | f(1,0,1,0) |
Карта размечается системой координат, соответствующих значениям входных переменных. Например, верхняя строка карты для функции от трех переменных соответствует нулевому значению переменной х1, а нижняя – ее единичному значению. Каждый столбец этой карты характеризуется значениями двух переменных: х2 и х3.
Обратим внимание на то, что координаты строк и столбцов следуют не в естественном порядке возрастания двоичных кодов, а в порядке 00, 01, 11, 10. Это код Грея. Изменение порядка следования наборов сделано для того, чтобы соседние наборы (отличающиеся между собой лишь цифрой одного разряда) были соседними в геометрическом смысле.
Ячейки, в которых функция принимает единичное значение, заполняются единицами. В остальные ячейки записываются нули. Процесс минимизации использует закон склеивания и заключается в формировании прямоугольников, содержащих по 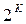 ячеек, где k – целое число. В прямоугольники объединяются соседние ячейки, соответствующие соседним элементарным произведениям. Те переменные, которые в прямоугольнике изменяют свои значения, исчезают.
ячеек, где k – целое число. В прямоугольники объединяются соседние ячейки, соответствующие соседним элементарным произведениям. Те переменные, которые в прямоугольнике изменяют свои значения, исчезают.
Совокупность прямоугольников, покрывающих все единицы, называется покрытием. Заметим, что одна и та же ячейка может покрываться несколько раз.
Рассмотрим несколько примеров.
|
| x3,х4 | ||||||
| х1,х2 | ||||||
|
| x3,х4 | |||||
| x1,х2 | |||||
|
| x3,х4 | ||||||
| x1,х2 | ||||||
|
Рис. 1.8. Карты Карно для функций четырех переменных.
Чем больше ячеек в прямоугольнике, тем меньше переменных содержится в соответствующем ему элементарном произведении. Например, для карты Карно, изображенной на рис. 1.8.а, прямоугольнику, содержащему четыре ячейки, соответствует произведение 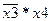 , а квадрату из одной ячейки – произведение
, а квадрату из одной ячейки – произведение 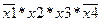 . Функция Q, соответствующая этому покрытию, имеет вид:
. Функция Q, соответствующая этому покрытию, имеет вид:
Q= 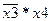 Ú
Ú 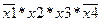 .
.
Формула, получающаяся в результате минимизации логической функции с помощью карт Карно, содержит сумму стольких элементарных произведений, сколько произведений имеется в покрытий.
Несмотря на то, что карты Карно изображаются на плоскости, соседство ячеек устанавливается на поверхности тора. Верхняя и нижняя границы карты Карно как бы «склеиваются», образуя поверхность цилиндра. При склеивании боковых границ образуется тороидальная поверхность. Так ячейки с координатами 1011 и 0011 (рис. 1.8,б) являются соседними и объединяются в один прямоугольник. Действительно, указанным ячейкам соответствует следующая сумма элементарных произведений:
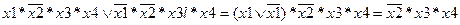 .
.
Аналогично объединяются и остальные четыре единичные ячейки. В результате их объединения получаем элементарное произведение 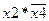 . Окончательно функция P, соответствующая покрытию, изображенному на рис. 1.8.б, имеет вид:
. Окончательно функция P, соответствующая покрытию, изображенному на рис. 1.8.б, имеет вид: 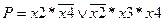
Карта Карно, показанная на рис.1.8.в, содержит единичные ячейки по углам. Все они являются соседними и после объединения дадут элементарное произведение 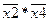 .
.
Рассмотренные примеры позволяют сформулировать последовательность действий, выполненных для минимизации логических функций с использованием карт Карно:
Изображается таблица для nпеременных и производится разметка ее сторон.
Ячейки таблицы, соответствующие наборам переменных, обращающих функцию в единицу, заполняются единицами, остальные – нулями.
Выбирается наилучшее покрытие таблицы прямоугольниками. Наилучшим считается такое покрытие, которое образовано минимальным числом прямоугольников, а если таких вариантов несколько, то из них выбирается тот, который дает максимальную суммарную площадь прямоугольников.
Сократить работу по минимизации иногда можно за счет работы не с самой заданной функцией, а с ее инверсией. Если число единиц в таблице истинности превышает половину числа комбинаций аргументов, то СДНФ для инверсии функции будет содержать меньше конъюнкций, чем СДНФ прямой функции. При аппаратной реализации к выходу схемы, обрабатывающей инверсию заданной функции, нужно подключить инвертор.
Пример.
Построить схему, реализующую функцию, заданную таблицей:
| a | b | c | Y | 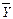
| a | B | c | y | 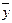
|
СДНФ требуемой функции: 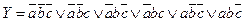
Для 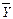 СДНФ будет значительно проще:
СДНФ будет значительно проще: 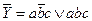 .
.
Последнее выражение более обозримо и легко минимизируется:
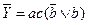 = ac, откуда
= ac, откуда 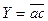 .
.
Для реализации необходим один двухвходовой элемент 2И–НЕ.
Рассмотрим особенности минимизации недоопределенныхфункций.
Недоопределенной называют функцию, значения которой при некоторых комбинациях не определены или, как говорят, безразличны. Например, при двоично-десятичном кодировании десятичные цифры представляются четырьмя двоичными разрядами. Из 16 возможных кодовых комбинаций используются лишь 10, остальные запрещены и никогда появиться не могут.
В таблице истинности не определенные значения функции отмечают прочерками.
Пример.
Построить схему, реализующую функцию Y, не определенную на наборах 000 и 111 и заданную таблицей.
 Y Y
| bc | |||||
| a | ||||||
| – | ||||||
| – | ||||||
При двух прочерках возможны четыре способа доопределения. Каждый из них дает работоспособную схему, но по аппаратурным затратам они будут разными. Самая простая схема получится, если доопределить функцию так, как показано на рис. 1.8,а.
В этом случае схема строится на двух ЛЭ: 2И и 2ИЛИ. (рис. 1.9.б)
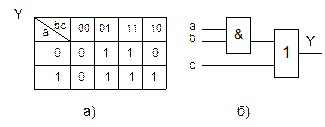
Рис. 1.9.Реализация недоопределенной функции.
Дата добавления: 2016-01-18; просмотров: 1085;
