Хозяйственной деятельности

Стохастический анализ выступает в качестве инструмента углубления детерминированного анализа факторов, по которым нельзя построить детерминированную модель.

Для изучения стохастической зависимости применяют следующие методы стохастического моделирования: группировка многомерных наблюдений, корреляционный и регрессионный анализ, дисперсионный анализ, методы причинного анализа, компонентный анализ.

Корреляционно-регрессионный анализ изучает взаимосвязи показателей хозяйственной деятельности, когда зависимость между ними не является строго функциональной и искажена влиянием посторонних, случайных факторов. В зависимости от количества исследуемых показателей различают парные и многофакторные модели корреляционно-регрессионного анализа.

Основной задачей корреляционно-регрессионного анализа является выяснение формы и тесноты связи между результативным и факторным показателями. Под формой связи понимают тип аналитической формулы, выражающей зависимость результативного показателя от изменений факторного. Различают связь прямую, когда с ростом (снижением) значений факторного показателя наблюдается тенденция к росту (снижению) значений результативного показателя. В противном случае между показателями существует обратная связь. Форма связи может быть прямолинейной (ей соответствует уравнение прямой линии), когда наблюдается тенденция равномерного возрастания или убывания результативного показателя, в противном случае форма связи называется криволинейной (ей соответствуют уравнения параболы, гиперболы и др.).

Основные модели корреляционного анализа: коэффициент парной корреляции, коэффициент частной корреляции, коэффициент множественной корреляции, коэффициент детерминации.

Линейный коэффициент парной корреляции (р) определяется по формуле:

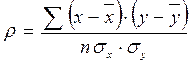
где 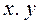— значения факторного и результативного показателей соответственно;

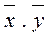— средние значения соответствующих показателей;

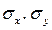— средние квадратические отклонения показателей х и у;

; ;

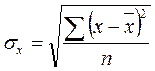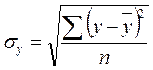где п — количество наблюдений в совокупности.

Значение коэффициента парной корреляции изменяется в пределах от 1 до +1. Знак «+» означает наличие прямой связи между показателями, знак «—» - обратной. Значение коэффициента от 0 до 1 характеризует степень приближения корреляционной зависимости между показателями и к функциональной. При 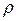= 1 между показателями существует функциональная связь. При 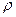= 0 линейная связь отсутствует.

Часто в анализе хозяйственной деятельности при изучении связи между показателями х и у требуется исключить воздействие третьего показателя z, выступающего как общий фактор изменения анализируемых показателей. Для этого используется коэффициент частной корреляции ( 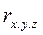), свойства которого совпадают со свойствами коэффициента парной корреляции:

;

где 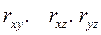- коэффициенты парной корреляции между соответствующими показателями.

Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором факторных показателей:

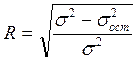, или ;

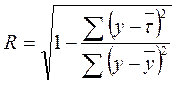где 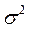- общая дисперсия эмпирического ряда, характеризующая общую вариацию результативного показателя (у) за счет факторов;

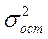- остаточная дисперсия в ряду у, отражающая влияние всех факторов, кроме х;

у - среднее значение результативного показателя, вычисленное по исходным наблюдениям;

х — среднее значение результативного показателя, вычисленное по уравнению регрессии.

Коэффициент множественной корреляции принимает только положительные значения в пределах от 0 до 1. Чем ближе значение коэффициента к 1, тем больше теснота связи, и, наоборот, чем ближе к 0, тем зависимость меньше. При значении R < 0,3 говорят о малой зависимости между величинами, при значении 0,3 < R < 0,6 — о средней тесноте связи, при R> 0,6 — о наличии существенной связи.

Квадрат коэффициента множественной корреляции называется коэффициентом детерминации (D): D=R². Коэффициент детерминации показывает, какая доля вариации результативного показателя связана с вариацией факторных показателей.

Математические модели корреляционного анализа в форме коэффициентов имеют ограниченные аналитические возможности. С их помощью невозможно определить закономерности формирования уровня результативного показателя под влиянием исследуемых факторов, оценить интенсивность их влияния, классифицировать факторы на основные и второстепенные. Для этих целей используются модели регрессионного анализа. Линейная модель (уравнение) регрессионного анализа может быть представлена в виде:

,

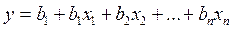где 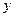- результативный показатель,

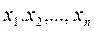- факторные модели,

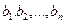- коэффициенты регрессии.

Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Коэффициенты 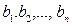показывают, на сколько единиц уровень результативного показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии характеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициентов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов.

Аналитические достоинства регрессионных моделей в том, что: во-первых, точно определяется фактор, по которому выявляются резервы повышения результативности хозяйственной деятельности; во-вторых, выявляются объекты с более высоким уровнем эффективности; в-третьих, возникает возможность количественно измерить экономический эффект от внедрения передового опыта и проведения организационно-технических мероприятий.