Средние показатели ряда динамики
Ряд динамики представляет статистическую совокупность показателей, варьирующих во времени. Для сравнения изменений того или иного показателя в разные периоды, в разных странах и т.п. необходимы обобщающие показатели в виде средних величин. Такими обобщающими характеристиками в рядах динамики являются:
- средний уровень ряда динамики;
- средний абсолютный прирост;
- средний темп роста,
- средний темп прироста.
Средний уровень ряда динамики рассчитывается неодинаково для различных видов рядов динамики. Кроме того, в исчислении средних величин по рядам динамики большое значение играет равенство (либо неравенство) промежутков времени между соседними уровнями.
Так, в интервальном ряду с равными периодами (интервалами) времени средний уровень рассчитывается по формуле средней арифметической простой:
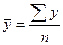 . (8.16)
. (8.16)
Например, по данным таблицы 8.9:
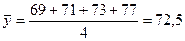 (млрд. руб.).
(млрд. руб.).
А в интервальном ряду с неравными периодами он рассчитывается по формуле средней арифметической взвешенной:
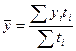 . (8.17)
. (8.17)
Таблица 8.10 – Динамика выпуска продукции
| Период времени | I кв. 2008 | IIкв. | |
| Выпуск продукции, млрд.руб. |
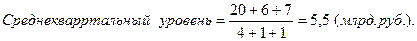
В моментных рядах динамики с равными интервалами времени средний уровень рассчитывается по формуле средней хронологической:
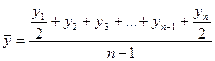 . (8.18)
. (8.18)
Таблица 8.11 – Динамика остатков готовой продукции на складе организации в первом квартале
| Дата | 01.01.08 | 01.02.08 | 01.03.08 | 01.04.08 |
| Остатки ГП на складе, млн. руб. |
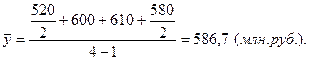
Для моментных рядов с неравными интервалами средний уровень определяется по формуле средней арифметической взвешенной, но в качестве весов принимается ti – количество отрезков времени, на протяжении которых сохраняется данный уровень:

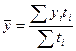 . (8.19)
. (8.19)
Например, необходимо определить среднегодовую стоимость основных средств по данным таблицы 8.12.
Таблица 8.12 – Динамика стоимости основных средств
| Дата | 01.01.08 | 01.04.08 | 01.05.08 | 01.09.08 | 01.01.09 |
| Стоимость ОС, млрд. руб. |
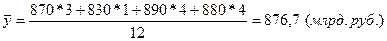
ti – в данном случае количество месяцев; за год Σ ti =12.
Средний абсолютный прирост рассчитывается как средняя арифметическая простая из абсолютных приростов (цепных):
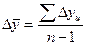 , (8.20)
, (8.20)
где n – число уровней ряда динамики;
n − 1 – число абсолютных приростов, которые могут быть получены по n уровням.
Либо учитывая накопление абсолютного прироста:
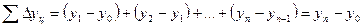 , (8.21)
, (8.21)
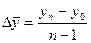 . (8.22)
. (8.22)
В нашем примере (таблица 8.9): 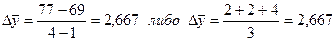 .
.
Важную роль в анализе рядов динамики играет средний темп роста. Наиболее часто он рассчитывается как средняя геометрическая из цепных темпов роста:
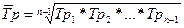 . (8.23)
. (8.23)
Используя выражения 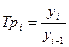 , можно получить другую формулу:
, можно получить другую формулу:
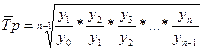 , т.е.
, т.е. 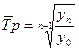 . (8.24)
. (8.24)
В нашем примере (таблица 8.9): 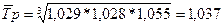
либо 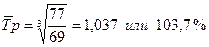 .
.
Средний темп прироста определяется на основе взаимосвязи между темпами роста и прироста.
Если данные о средних темпах роста выражены в виде коэффициента:
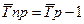 (8.25)
(8.25)
1,037 – 1 = 0,037,
а если данные приводятся в процентах, то:
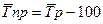 (8.26)
(8.26)
103,7 – 100 = 3,7 (%).
По средним показателям в нашем примере можно сделать следующие выводы:
а) размер среднегодовой прибыли за исследуемый период составляет 72,5 млрд. руб.;
б) из года в год прибыль увеличивается в 1,037 раза;
в) за каждый год прибыль возрастает в среднем на 2,667 млрд. руб. или на 3,7 %.
Дата добавления: 2016-01-16; просмотров: 1356;
