РАДИОЭЛЕКТРОННЫХ СРЕДСТВ

Проектирование радиоэлектронных средств с применением ЭВМ требует описания этого объекта на языке математики в виде, удобном для его алгоритмической реализации.

Математическое описание проектируемого объекта называют математической моделью.

Математическая модель – это совокупность математических элементов (чисел, переменных, векторов, множеств и т.п.) и отношений между ними, которые с требуемой для проектирования точностью описывают свойства проектируемого объекта.

2.1. Уровни абстрагирования и формы представления
моделей проектируемых объектов

На каждом этапе проектирования используется свое математическое описание проектируемого объекта, сложность которого должна быть согласована с возможностями анализа на ЭВМ, что приводит к необходимости иметь для одного объекта несколько моделей различного уровня сложности.

В общей теории математического моделирования математическую модель любого объекта характеризуют внутренними, внешними, выходными параметрами и фазовыми переменными.

Внутренние параметры модели определяются характеристиками компонентов, входящих в проектируемый объект, например номиналы элементов принципиальной схемы. Если проектируемый объект содержит n элементарных компонентов, то и его математическая модель будет определяться параметрами w₁...w_n, которые образуют вектор внутренних параметров:

.

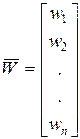Каждый из параметров w_i, в свою очередь может быть функцией, вектором или еще более сложным математическим функционалом в зависимости от объекта проектирования.

Выходные параметры модели – это показатели, характеризующие функциональные, эксплуатационные, конструкторско-технологические, экономические и другие характеристики проектируемого объекта. К таким показателям могут относиться коэффициенты передачи, масса и габариты проектируемого объекта, надежность, стоимость и т.п.

Вектор выходных параметров модели обозначают:

.

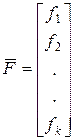Понятия внутренних и выходных параметров инвариантны, при моделировании на более сложном уровне выходные параметры могут стать внутренними и наоборот.

Пример: Сопротивление резистора является внутренним параметром при моделировании усилительного устройства, компонентом которого он является, но это же сопротивление будет выходным параметром при моделировании самого резистора, что требуется при пленочном его исполнении.

Внешние параметры модели – это характеристики внешней по отношению к проектируемому объекту среды, а также рабочие управляющие воздействия.

.

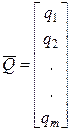Вектор внешних параметров в общем случае содержит множество самых различных составляющих.

Уравнения математической модели могут связывать некоторые физические характеристики компонентов, которые полностью характеризуют состояние объекта, но не являются выходными или внутренними параметрами модели. Такие характеристики называют фазовыми переменными. Минимальный по размерности вектор фазовых переменных, полностью характеризующий работу объекта проектирования, называют базисным вектором:

.

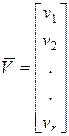Пример. Усилитель мощности.

Внутренние параметры: номиналы элементов электрической схемы.

Выходные параметры: выходная мощность и коэффициент передачи.

Фазовые переменные: узловые потенциалы схемы.

Использование вектора фазовых переменных позволяет упростить алгоритмическую реализацию программ, составляющих уравнения математической модели устройства.

В общем случае выходные параметры 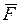представляются операторами от векторов 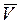, , 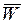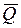и могут быть определены из решения системы уравнений математической модели устройства. Математическая модель любого радиотехнического объекта может быть представлена в виде следующих систем уравнений:

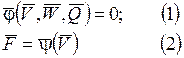
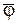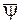где и – операторы, определяющие вид систем уравнений модели.

Система уравнений (1) может представлять собой систему линейных алгебраических уравнений, нелинейных уравнений различного вида, дифференциальных в полных или частных производных и представляет собой собственно математическую модель проектируемого объекта. В результате решения системы (1) определяются действующие в устройстве фазовые переменные 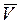. Система уравнений (2) определяет зависимость выходных параметров объекта от фазовых переменных .

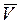По способу получения математические модели РЭС делят на физические и формальные.

Физические модели получают на основе изучения физических закономерностей функционирования проектируемого объекта, поэтому структура уравнений и параметры модели имеют ясное физическое толкование.

Формальные модели получают на основе измерения и установления связи между основными параметрами объекта в тех случаях, когда физика работы его известна недостаточно полно.

Как правило, формальные модели требуют большого числа измерений и по своей природе являются локальными, справедливыми вблизи тех режимов, в которых производились измерения. В литературе иногда такие модели называют моделями «черного ящика».

С точки зрения учета инерционности РЭС при проектировании различают модели статические и динамические.

Статические модели отражают состояние объекта проектирования при неизменных внешних параметрах и не учитывают его переходные характеристики.

Динамические модели дополнительно отражают переходные процессы в объекте, происходящие при изменении во времени внешних параметров.

Для синтеза адекватных реальному объекту моделей большинства радиотехнических устройств базовый набор должен содержать по крайней мере пять типов сосредоточенных схемных элементов:

1) резистор,

2) конденсатор,

3) индуктивность,

4) источник напряжения,

5) источник тока.

Таблица 2.1

Компонентные уравнения базовых схемных элементов

Базовые элементы	Компонентные уравнения
в операторной форме	во временной форме	в частотной форме
1. Резистор:
Линейный	u=Ri(p)	u(t)=Ri(t)	u(ω)=Ri(ω)
управляемый током	u=r(i)i(p)	U(t)=R[i(t)]i(t)	u(ω)=R[i(ω)]i(ω)
управляемый напряжением	i=G(u)u(p)	i(t)=G[u(t)]u(t)	i(ω)=G[u(ω)]u(ω)
2. Конденсатор:
Линейный	i=Cpu(p)	i(t)=Cdu/dt	i(ω)=jωCu(ω)
управляемый током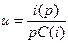
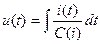
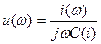
управляемый напряжением	i=pC(u)u(p)		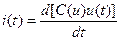i(ω)=jωC(u)u(ω)
3. Индуктивность:
Линейная	u=Lpi(p)		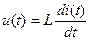u(ω)= jωLi(ω)
управляемая током	u=pL(i)i(p)		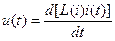u(ω)= jωL(i)i(ω)
управляемая потоком	u=pФ(p)		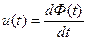u(ω)= jωФ(ω)
4. Источник напряжения:
независимый	u=E(p)	U=E(t)	u(ω)=E(ω)
управляемый током iab	u=E[iab(p)]	U(t)=E[iab(t)]	u(ω)=E[iab(ω)]
управляемый напряжением uab	u=E[uab(p)]	U(t)=E[uab(t)]	u(ω)=E[uab(ω)]
5. Источник тока:
независимый	i=I(p)	i=I(t)	i(ω)=I(ω)
управляемый током iab	i=I[iab(p)]	i(t)=I[iab(t)]	i(ω)=I[iab(ω)]
управляемый напряжением uab	i=I[uab(p)]	I(t)=I[uab(t)]	i(ω)=I[uab(ω)]