Составление ведомости прямых и кривых

Зная румб начального направления, пикетажные значения вершин углов поворота и точек начала и конца обеих кривых, название (правый и левый) и величину углов поворота, составляют ведомость прямых и кривых, которая необходима для контроля всех вычислений, связанных с положением трассы в плане. Кроме того, она является основным документом для разбивки трассы на местности. Образец ведомости прямых и кривых для рассматриваемого в учебно-методическом пособии случая приведен в прил.4.

Графа 1 – номер точек – заполняется через строчку названиями точек переломов трассы в плане (НТ, ВУ1, ВУ2, КТ), где НТ – начало трассы; КТ – конец трассы.

Графа 2 заполняется пикетажным обозначением главных точек трассы в плане. Эти значения одинаковы для всех вариантов заданий.

Графы 3 и 4 заполняются значениями углов поворота из индивидуальных данных.

Графы 5 – 9 заполняются значениями элементов обеих кривых, вычисленных в подразделе «Расчет основных элементов горизонтальных круговых кривых», с подсчетом сумм кривых и домеров.

Графы 10 и 11 заполняются данными вычислений пикетажных значений точек НК и КК, выполненных в подразделе «Расчет пикетажных значений главных точек кривых».

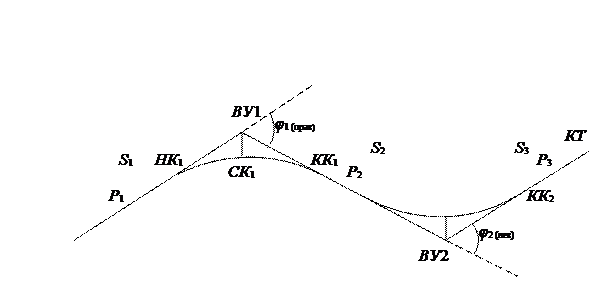
Графа 12 заполняется величинами прямолинейных участков трассы Р, оставшихся после вписывания обеих круговых кривых. Способ их вычисления будет понятен при рассмотрении схемы трассы с расчетными элементами (рис. 2.3).

Рис. 2.3. Схема трассы с расчетными элементами

Длины прямых вставок Р₁, Р₂ и Р₃ вычисляются следующим образом:

• Длина прямой вставки, расположенной на стороне НТ–ВУ1, определяется разностью пикетажных значений начала первой кривой и начала трассы. Для нашего примера НТ имеет пикетажное значение ПК0, поэтому Р₁ = НК₁ – НТ.

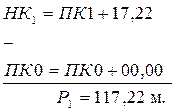
• Длина вставки на сторону ВУ1 – ВУ2 вычисляется разностью пикетажных значений начала второй круговой и конца первой круговой кривой: Р₂ = НК₂ – КК₁.

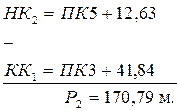
Так как по условиям задания общая длина трассы должна быть равна 10 пикетам, то прямая вставка Р₃ определится разностью пикетажных значений КТ и конца второй круговой кривой:

Р₃=КТ–КК₂; КТ=ПК10+00,00.

В строчке «Сумма» подсчитывается общая длина трех прямых вставок.

Графа 13 заполняется значениями расстояний между вершинами углов поворота S₁, S₂ и S₃ (см. рис. 2.3). Значения S₁, S₂ и S₃ вычисляют по следующим формулам:

S₁=ВУ1;(2.10)

S₂=ВУ2–ВУ1+ Д₁;(2.11)

S₃= КТ–ВУ2+Д₂ (2.12)

или

S₁=Р₁+ Т₁; (2.13)

S₂=Т₁+Р₂+Т₂;(2.14)

S₃=Т₂+ Р₃. (2.15)

Для нашего примера получим следующие значения.

По формулам (2.10)–(2.12)

S₁=230,63 м;

S₂=718,70 м–230,63 м+2,20 м=490,27 м;

S₃= 1000 м–718,70 м+6,70 м=288,00 м.

По формулам (2.13)–(2.15)

S₁=117,22 м+113,41 м=230,63 м;

S₂=113,81 м+170,79 м+206,07 м=490,27 м;

S₃=206,07 м+81,93 м=288,00 м.

В строчку «Сумма» необходимо вписать общую длину всех трех расстояний между вершинами углов поворота (S₁+S₂+S₃).

Графа 14 заполняется значениями дирекционных углов сторон трассы. Для вычисления дирекционных углов сторон ВУ1–ВУ2 и ВУ2–ПК10 используют исходный румб начальной стороны НТ–ВУ1 и значения углов поворота трассы. Переведя исходный румб в дирекционный угол, вычисляют дирекционные углы всех последующих сторон по правилу: дирекционный угол последующего направления трассы равен дирекционному углу предыдущего направления плюс правый или минус левый угол поворота трассы.

В нашем случае r_исх=ЮВ: α=47^º20^'; φ₁=18^º20^´; φ₂=23^º05^´.

Так как название румба ЮВ, то α_н=180º–r_исх=132º40'.

	для направления (НТ–ВУ1)     для направления (ВУ1–ВУ2)
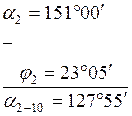
	для направления (ВУ2–КТ)

Вычисленные дирекционные углы записываются в колонку 14, от их значений переходят к румбам и заносят их в графу 15 ведомости.

Контроль правильности вычисления дирекционных углов:

;

.

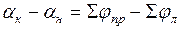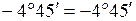После заполнения ведомости прямых и кривых производится контроль расчетов по формуле

SP+ SK= SS-SД= L, (2.16)

где L – общая длинна трассы (1000 м).

Значения составляющих элементов этой формулы берём из графы «Сумма» ведомости прямых и кривых. Для рассматриваемого случая контроль расчетов будет следующим:

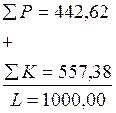
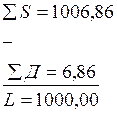
Допустимое значение расхождений L также равно 2 см, оно объясняется округлением при расчетах основных элементов кривых.