Виды средних величин

В статистике используют различные виды средних величин, которые делятся на два больших класса:

• степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадратическая, средняя кубическая);

• структурные средние величины (мода, медиана).

Для вычисления степенных средних величин необходимо использовать все имеющиеся значения признака. Мода и медиана определяются лишь структурой распределения, поэтому их называют структурными, позиционными средними. Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной величины невозможен или нецелесообразен.

Самый распространенный вид средней величины – средняя арифметическая. Под средней арифметической величиной понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности. Вычисление данной величины сводится к суммированию всех значений варьирующего признака и делению полученной суммы на общее количество единиц совокупности. Например, пять рабочих выполняли заказ на изготовление деталей, при этом первый изготовил 5 деталей, второй – 7, третий – 4, четвертый – 10, пятый– 12. Поскольку в исходных данных значение каждого варианта встречалось только один раз, для определения средней выработки одного рабочего следует применить формулу простой средней арифметической:

т. е. в нашем примере средняя выработка одного рабочего равна

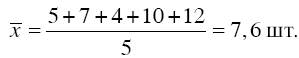
Пример.

По состоянию на 14 октября имеются следующие данные о расходе металла 8 рабочими (кг): 17,2; 19,0; 20,0; 17,0; 18,0; 19,8; 18,0; 18,6 Для того чтобы определить средний расход металла на одного рабочего, необходимо общий расход металла разделить на число рабочих:

кг.

Наряду с простой средней арифметической величиной изучают среднюю арифметическую взвешенную величину. Если данные представлены в виде дискретного ряда распределения, то расчет средней производится по формуле средней арифметической взвешенной

,

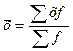где х – значение признака;

f – частота повторения соответствующего признака (веса).

Например, рассчитаем средний возраст студентов в группе из 20 человек, возраст которых варьируется от 18 до 22 лет, где x_i – варианты усредняемого признака, f_i – частота, которая показывает, сколько раз встречается i-е значение в совокупности (табл.1).

Исходная таблица

Таблица 1.

Средний возраст рассчитаем по формуле простой средней:

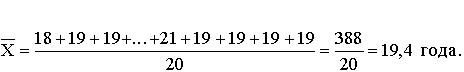
Сгруппируем исходные данные по возрасту студентов. Получим следующий ряд распределения:

Таблица 5.1