Операторы физических величин. Средние значения.

Уравнение Шредингера.

Чтобы записать уравнениеШредингера (1926), рассмотрим сначала схему вывода дисперсионного уравнения для плоской монохроматической волны:

исходное волновое уравнение:

, (2.1)

решение – плоская волна:

, (2.1a)

действие операторов 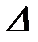и :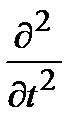

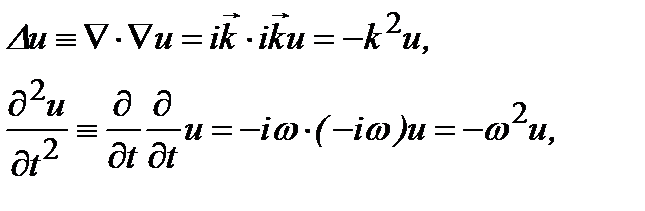(2.1б)

подстановка (2.1б) в исходное уравнение:

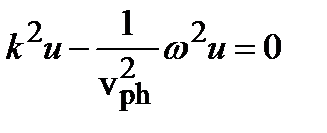. (2.1в)

Отсюда следует дисперсионное уравнение, связывающее частоту и волновое число плоской волны (2.1а):

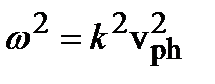. (2.2)

Из (2.1б) видно, что действие оператора «набла» на выражение для плоской волны приводит к умножению на :

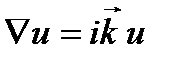, (2.3)

тогда как действие оператора 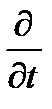приводит к умножению на :

. (2.4)

Справедливо также обратное: умножение выражения для плоской волны на волновой вектор 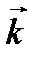эквивалентно действию оператора :

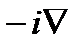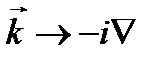, (2.3а)

а умножение на частоту 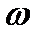– действию оператора :

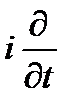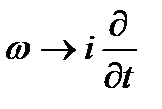. (2.4а)

Чтобы записать уравнение Шредингера для волновой функции, воспользуемся схемой (2.1-2.2), идя «снизу вверх» – от (2.2) к (2.1). «Дисперсионным уравнением», связывающим частоту и волновой вектор волн де Бройля, является формула для полной энергии частицы:

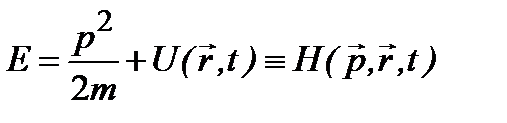, (2.5)

где 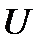– потенциальная энергия частицы, 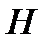– функция Гамильтона. Действительно, пользуясь соотношениями (1.49), (1.50), из (2.5) получаем:

. (2.5а)

Умножим формально обе части (2.5а) на волновую функцию:

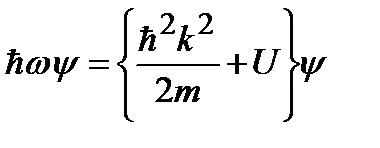. (2.5б)

Заменяем затем 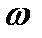и 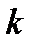на операторы согласно (2.3а), (2.4а). Тогда приходим к искомому уравнению Шредингера:

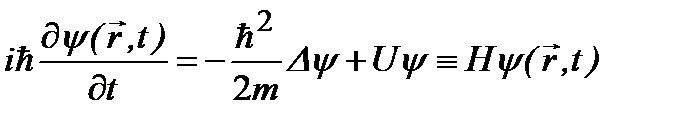, (2.6)

где величина

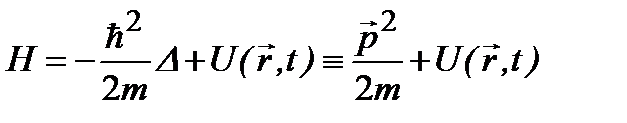(2.7)

оператор Гамильтона, или гамильтониан. Шляпка над буквой означает соответствующий оператор. В формуле (2.7) на основе соотношений (1.49), (2.5) и (2.3а), введен оператор импульса:

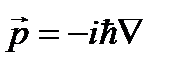.(2.8)

Уравнение (2.6) - нестационарное уравнение Шредингера.

Если потенциальная энергия 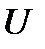не зависит от времени, то оператор Гамильтона (2.7) зависит только от координат. В этом случае состоянияквантовой системы называются стационарными. Для таких состояний пространственная и временная зависимости в волновой функции могут быть разделены: 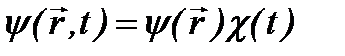. Тогда из (2.6) получаем: 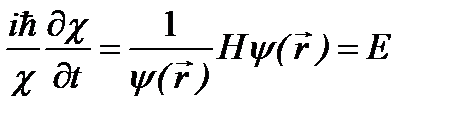, где Е – постоянная разделения, имеющая смысл энергии состояния. Отсюда следует, что временная зависимость волновой функции согласно уравнению 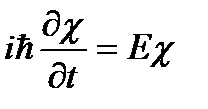является вполне определенной: 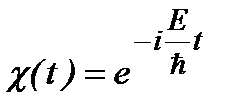. Пространственная зависимость волновой функции описывается уравнением:

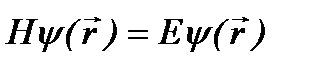. (2.9)

Таким образом, для стационарных состояний волновая функция имеет вид:

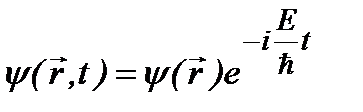. (2.10)

Плотность вероятностей таких состояний не зависит от времени: 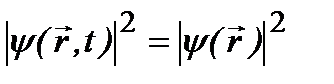. Поэтому они называются стационарными. Уравнение (2.9) - стационарное уравнение Шредингера, которое часто записывают в эквивалентной форме:

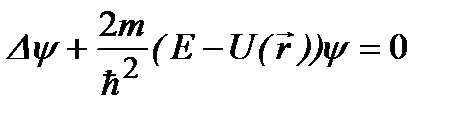. (2.11)

Уравнение Шредингера линейно относительно волновой функции. Поэтому справедливпринцип суперпозиции решений. Линейная комбинация нестационарных решений уравнения Шредингера также является нестационарным решением. Суперпозиция стационарных решений с разными значениями энергии, в общем, может не быть стационарным решением. Пусть

. (2.12)

В этом случае плотность вероятности зависит от времени:

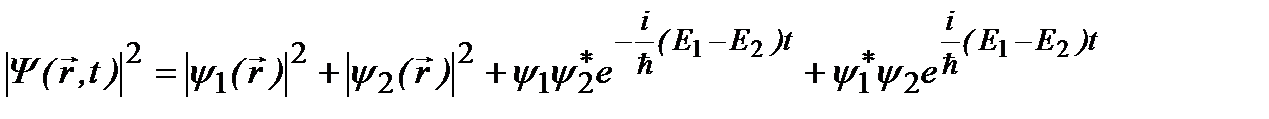. (2.12a)

Видно, что плотность вероятности периодически изменяется с частотой 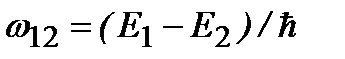, которая совпадает с боровской частотой перехода между стационарными состояниями.Если система находится в одном из стационарных состояний, то плотность вероятностей в этом состоянии не зависит от времени – ее энергия имеет некоторое определенное значение, так что система не излучает и не поглощает энергию. Таким образом, квантовая механика атома не противоречит законам электродинамики.

Условие нормировки волновой функции вытекает из уравнения Шредингера: умножая уравнение (2.8) слева на функцию 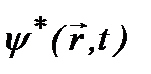, а комплексно–сопряженное уравнение – на 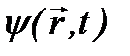, и затем, вычитая полученные выражения, приходим к уравнению:

.

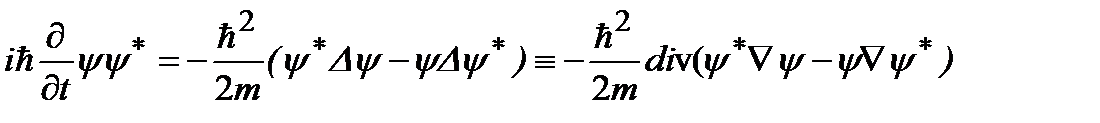Величина 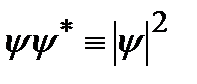определяет плотность вероятности. Вектор

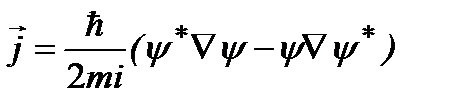(2.13)

интерпретируется как вектор плотности потока вероятности. Таким образом, приходим к уравнению, имеющему смысл уравнения сохранения вероятности:

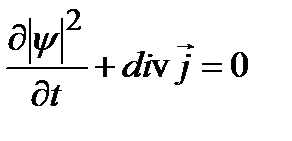. (2.13a)

После интегрирования по всему пространству: 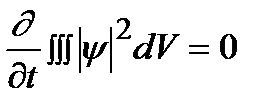, так как 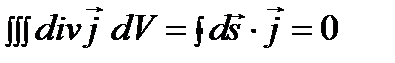, где 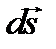– элемент поверхности Таким образом, 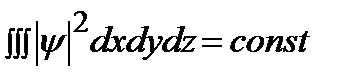. По смыслу волновой функции эта постоянная должна быть равна единице.

Физически приемлемые решения уравнения Шредингера требуют выполнения определенных условий. Волновая функция должна быть однозначной, непрерывной и ограниченной вместе со своими первыми производными.

Уравнение Шредингера является нерелятивистским и не учитывает важного свойства микрочастиц – их спина. В этом его недостаток. Кроме того, уравнение Шредингера является феноменологическим, поскольку внешние воздействия на частицу (поля) задаются классически с помощью выражения для потенциальной энергии. Такой подход аналогичен описанию распространения электромагнитных волн в среде, свойства которой задаются с помощью феноменологического показателя преломления.

Уравнение Шредингера в форме (2.9) показывает, что в результате воздействия оператора Гамильтона (2.7) на волновую функцию получается та же волновая функция, помноженная на постоянное значение энергии. Тогда говорят, что поставлена задача на собственные значения оператора, в данном случае, оператора Гамильтона. При соблюдении физических требований на волновую функцию и при соответствующих граничных условиях решение этой задачи существует не при любых значениях постоянной Е, а лишь при строго определенных значениях, образующих энергетический спектр рассматриваемой системы: 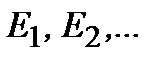Эти значения называются собственными значениями энергии, а соответствующие им волновые функции 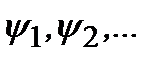называются собственными функциями.Квадрат модуля собственной волновой функции 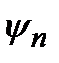определяет плотность вероятности того, что квантовая система находится в элементе объема dV вблизи точки 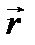в состоянии со значением энергии 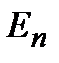. По формуле полной вероятности:

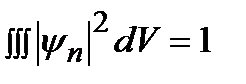. (2.14а)

Рассмотрим теперь уравнение Шредингера (2.9) для собственной функции 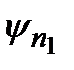с собственным значением энергии 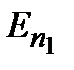и для собственной функции 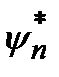с собственным значением 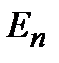По физическому смыслу собственные значения энергии должны быть действительными величинами. Будем считать, что эти значения энергии различны:

.

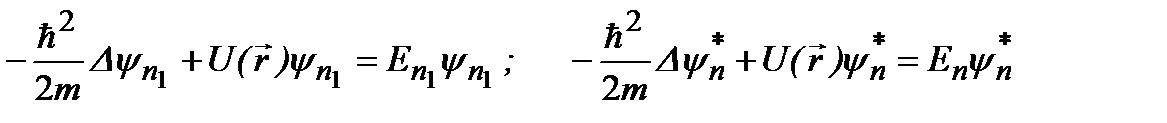Умножим первое из этих уравнений на 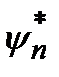, а второе – на 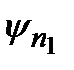, и затем вычтем одно из другого: 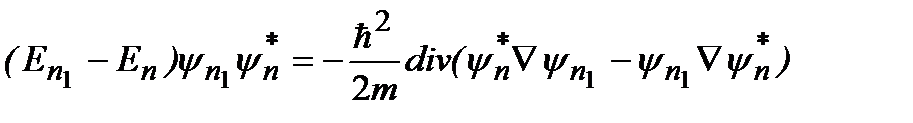. Интегрируя по всему пространству с использованием теоремы Гаусса–Остроградского, получаем: 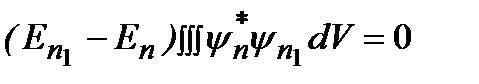. Так как, по условию, 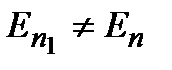, то отсюда следует соотношение: 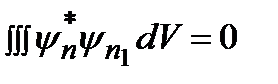. Это соотношение показывает, что собственные волновые функции, отвечающие разным собственным значениям, взаимно ортогональны.

Вместе с формулой (2.14а) полученное соотношение может быть записано единым образом как условие ортонормировкисобственных волновых функций:

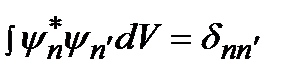, (2.14)

где 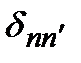– символ Кронекера: .

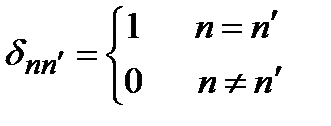В квантовой механике принимается, что измеряемые на опыте значения физических величин, так же как значения энергии, являются собственными значениями соответствующих операторов. Для определения этих собственных значений необходимо данной физической величине сопоставить соответствующий оператор (Борн, 1926). Таким образом, если F – некоторая физическая величина, то ей сопоставляется оператор 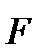, для которого аналогично (2.9) ставится задача на собственные значения. Эти собственные значения образуют спектр величины F. В общем спектр может быть дискретным, составленным из дискретных значений 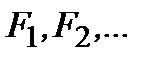, и может быть непрерывным,простирающимся по всей области задания величины F. Для удовлетворения принципу суперпозиции квантовые операторы должны быть линейными. 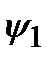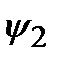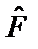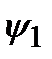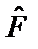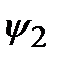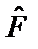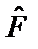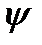Такие операторы определяются условиями: ( + ) = = + , (а )=а , где 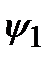, 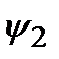– произвольные функции, а – произвольная постоянная.

В случае дискретного спектра задача на собственные значения ставится аналогично (2.9):

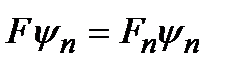. (2.15)

Собственные функции удовлетворяют условию ортонормировки (2.14). Если квантовая система описывается произвольной волновой функцией 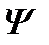, то в результате измерения величины F должно получиться одно из собственных значений 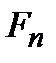, которому соответствует собственная функция 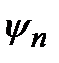. Отсюда следует, согласно принципу суперпозиции, что волновая функция 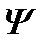, в общем, должна быть представлена в виде линейной комбинации собственных функций 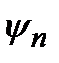оператора :

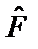, (215а)

где 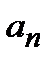– некоторые коэффициенты. Используем условие нормировки волновой функции и условие ортонормировки собственных функций (2.14). В результате получаем:

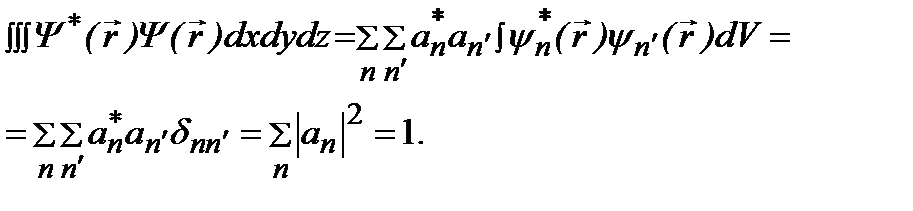(2.16)

Отсюда следует, что величину 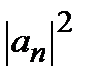можно интерпретировать как вероятность того, что величина F имеет значение 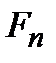. Умножая (2.15а) на 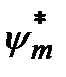и используя условие (2.14), находим, что коэффициенты разложения (2.15а) определяются формулой

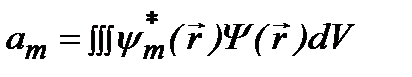. (2.16а)

Среднее значениевеличины F определяется по общим правилам теории вероятностей как сумма собственных значений, умноженных на соответствующую им вероятность:

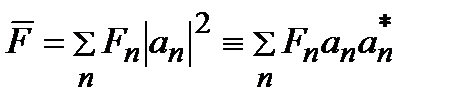. (2.17)

Преобразуем это выражение, используя соотношения (2.16а), (2.15), (2.15а):

.

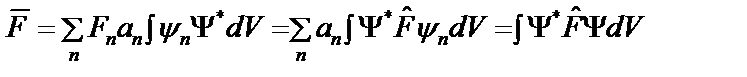(2.17а)

Отсюда следует, что среднее значение любой физической величины можно вычислить в координатном представлении волновой функции, если известен соответствующий оператор в этом представлении. Например, среднее значение импульса равно: Когда система находится в состоянии, описываемом собственной волновой функцией, то среднее значение величины F совпадает с его собственным значением:

.

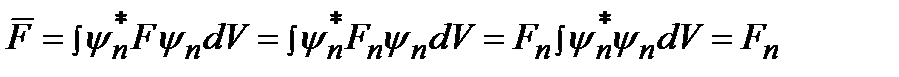В этом случае коэффициент (при фиксированном n), а остальные коэффициенты обращаются в нуль.

Собственные значения физических величин, а также их средние значения являются действительными величинами. Это накладывает ограничения на свойства квантово–механических операторов. Вещественность среднего значения оператора означает, что должно выполняться интегральное соотношение:

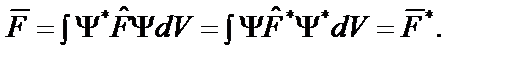
В этом случае говорят, что оператор 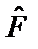– эрмитов оператор. Более общее условие эрмитовости оператора определяется соотношением:

,

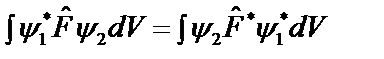где 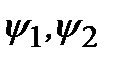– произвольные функции. Таким образом, операторы физических величинв квантовой механике должны быть линейнымииэрмитовыми.

В стационарных состояниях собственные волновые функции являются функциями вида: 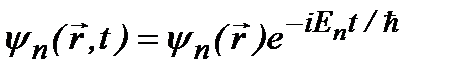. В этом случае состояние, описываемое функцией с разложением (2.15а), не является стационарным. Подставляя такую функцию в (2.17а), получаем:

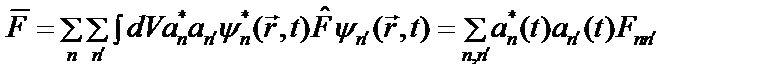. (2.17б)

Величина

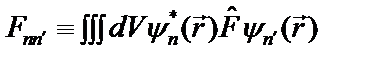(2.17в)

называется матричным элементом оператора 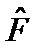, соответствующим переходу из состояния n в состояние 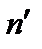. Коэффициенты 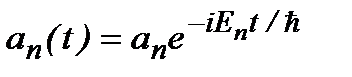. Временная зависимость в (2.17б) определяется множителем , где 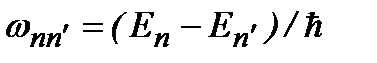– частота перехода. Совокупность всех матричных элементов образует матрицу оператора 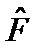. Диагональные элементы этой матрицы

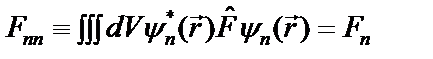(2.17г)

являются собственными (средними) значениями величины F в состоянии с волновой функцией .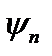

Примерами величины F с непрерывным спектром могут служить координата и импульс частицы. Если F, например, координата x, или функция координат F(x,y,z),то по смыслу волновой функции и согласно определениям (1.71) и (2.17а), оператором координаты (или функции координат) является операция умножения на эту координату (или функцию координат). Если величина F – импульс, то для нахождения среднего значения импульса, а также дисперсии необходимо учитывать определение оператора импульса (2.8). Если F – функция координат и импульса вида 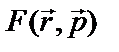, то этой функции в координатном представлении сопоставляется оператор 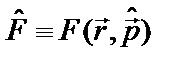. В импульсном, или р–представлении, оператор импульса сводится к умножению на этот импульс, а координате отвечает оператор: .

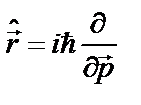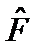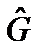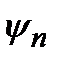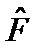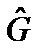Если две физические величины F и G имеют определенные значения, то им соответствуют состояния, описываемые собственными функциями операторов и . Очевидно, что величины F и G будут иметь одновременно определенные значения, если этим значениям отвечает одна и та же, общая собственная функция. Таким образом, если – общая собственная функция операторов и , то 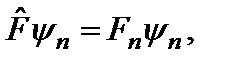. Подействуем теперь на первое их этих соотношений оператором 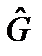, а на второе соотношение – оператором 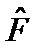. В результате полу-чаем:

.

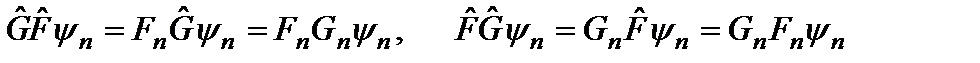Отсюда следует: 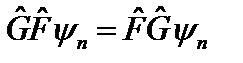. Так как произвольная волновая функция является линейной комбинацией функций 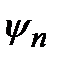, то такое же соотношение выполняется и в случае любой волновой функции 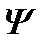. Это соотношение записывается в виде символического равенства:

.

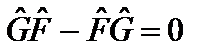О таких двух операторах говорят, что они коммутируютдруг с другом, т.е. результат действия двух таких операторов на некоторую функцию не зависит от последовательности действия этих операторов. Таким образом, если операторы имеют общие собственные функции, то они коммутируют друг с другом.Справедливо также обратное утверждение: если операторы коммутируют, то они имеют общие собственные функции.Физически это означает, что соответствующие физические величины могут одновременно иметь определенные измеряемые значения. Например, волновая функция 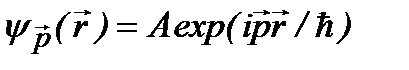является общей для операторов 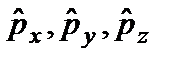. Это значит, что проекции вектора импульса на все три декартовы оси координат могут иметь одновременно определенные значения. Вместе с тем, координата и соответствующий ей оператор проекции импульса не коммутируют. Например, 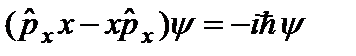, или в символической форме 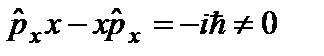. Это отражает уже известный факт, устанавливаемый соотношениями неопределенностей, что координата и соответствующая проекция импульса не могут одновременно иметь определенные значения.

Разность 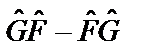называют коммутатором операторов 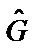и 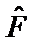. Для коммутатора используют обозначение: .

Волновые функции системы, находящейся, например, в центральном поле сил, обладают важным свойством, называемым четностью. Это свойство связано с преобразованием инверсии - изменение знаков всех декартовых координат на обратные: . Такое преобразование, эквивалентное замене правой системы координат на левую, не нарушает вероятностного смысла волновой функции, при этом оператор Гамильтона не должен менять свой знак: 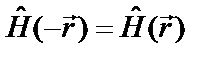. Очевидно, это возможно в потенциальном поле, для которого 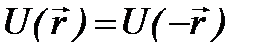. В соответствии с преобразованием инверсии вводят оператор инверсии 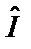, который изменяет знаки координат волновой функции на обратные: 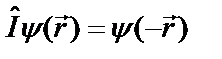. Рассмотрим задачу на собственные значения оператора инверсии: , где I – собственное значение. Подействуем еще раз оператором 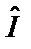и учтем, что при двукратном применении этого оператора координаты волновой функции не изменяются: 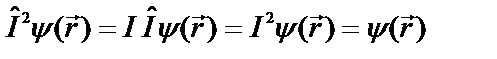. Отсюда следует, что 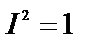, т.е. оператор инверсии имеет два собственных значения: 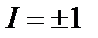. Это значит, что существуют волновые функции, которые не изменяют своего знака при инверсии координат: 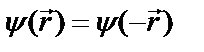, есть также волновые функции, изменяющие свой знак: . Первые функции называются четными, а вторые – нечетными. Говорят также о функциях, соответственно, с положительнойи отрицательной четностью.

Потенциальные «ямы» и «барьеры»

Среди различных задач квантовой механики простейшими являются одномерные задачи, в которых рассматривается движение частицы в каком-то одном направлении, например, вдоль оси x. Стационарное уравнение Шредингера (2.11) в одномерном случае имеет вид:

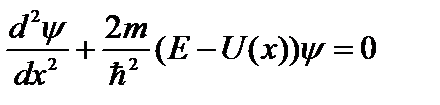. (2.20)

Состояния движущейся частицы зависят от характера ее потенциальной энергии 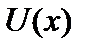. На рис.2.1 изображена потенциальная яма. Она характеризуется тем, что в некоторой области потенциальная энергия имеет минимум. На рис.2.2 изображен потенциальный барьер, который представляет собой область пространства, где потенциальная энергия имеет максимум.

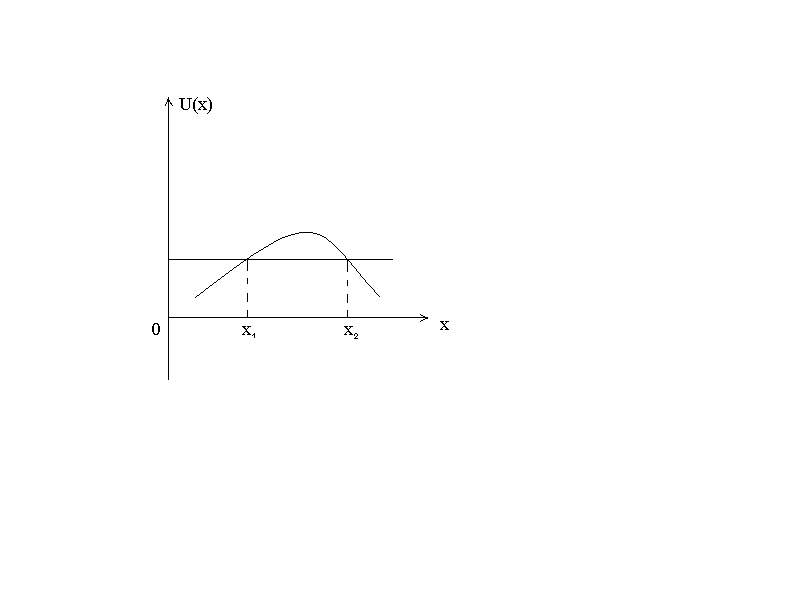
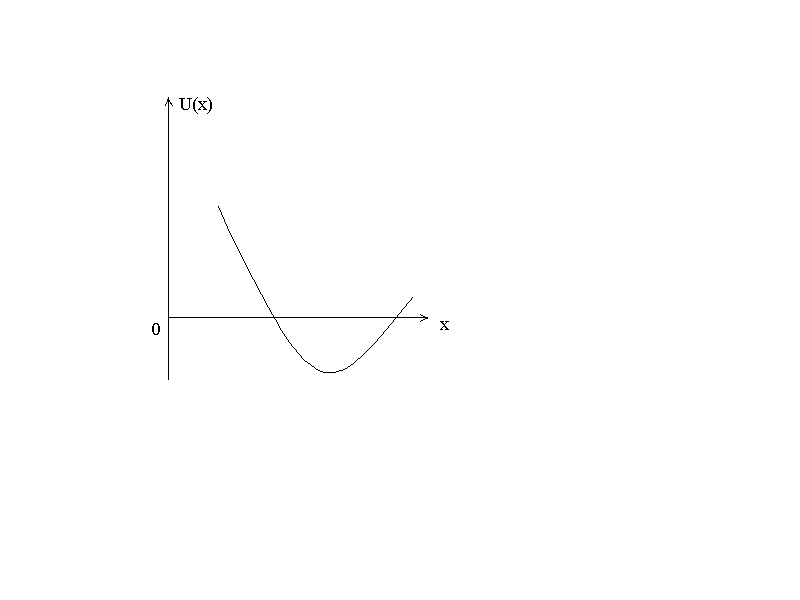
Рис.2.1 Рис.2.2

Нахождение волновых функций в произвольных полях из уравнения (2.20) является сложной задачей, которая может быть решена лишь приближенными методами. Одним из таких методов является квазиклассический метод Вентцеля–Крамерса–Бриллюэна (ВКБ). Однако существует класс модельных задач, которые решаются точно. Это, прежде всего, задачи с прямоугольной ямой (рис.2.3) и прямоугольным барьером (рис.2.4а, 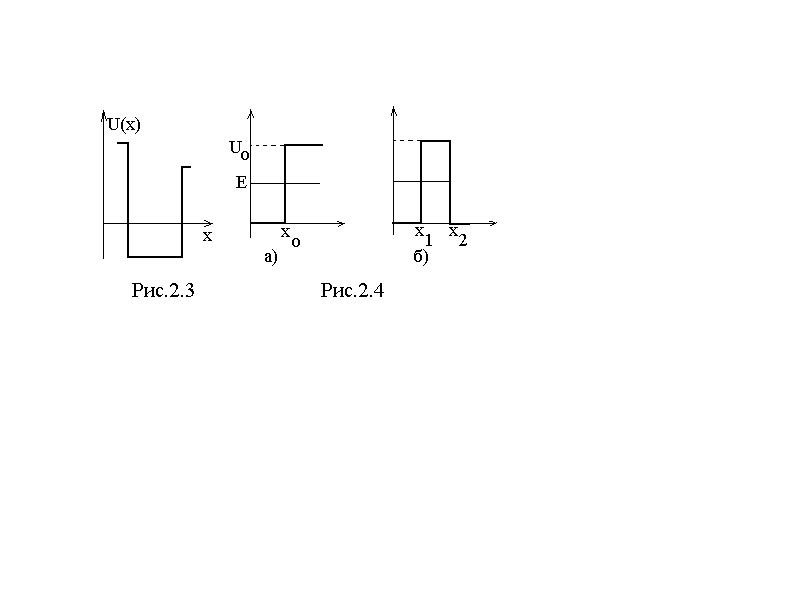б). Такие задачи являются модельными, но они позволяют получить качественные, а иногда и количественные оценки состояний частицы в более реальных случаях. С этой целью гладкие по-тенциальные кривые аппроксимируют ломаными из горизонтальных и вертикальных отрезков. Таким образом, кривые, например, на рисунках 2.1 и 2.2 можно представить в виде суммы прямоугольных ям (или барьеров). Зная результат для каждой такой области, можно, просуммировав, получить приближенный результат для гладких зависимостей .

В каждой из областей оси x, где потенциальная энергия постоянна, можно найти точное решение уравнения (2.20). Характер решения зависит от знака величины 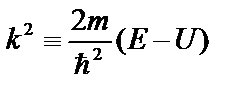. Например, в случае свободной частицы, потенциальная энергия которой равна нулю, волновая функция, как решение уравнения (2.20), описывает волны типа 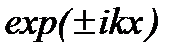, бегущие в положительном (знак плюс) или отрицательном (знак минус) направлении оси х, где волновое число .При этом надо помнить о временном множителе 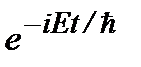. Если потенциальная энергия частицы не равна нулю, то при (полная энергия частицы превышает потенциальную энергию) решение также представляет собой волны, бегущие в противоположных направлениях. В случае 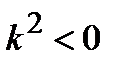(т.е. E<U) общее решение содержит комбинации решений вида 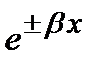, где .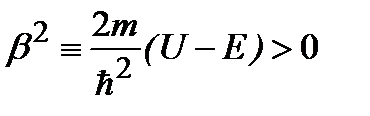

По представлениям классической механики частица не может находиться в области . По квантовым представлениям имеется определенная вероятность нахождения частицы и в этой «запрещенной» области. Этот эффект связан со свойством непрерывности волновой функции. Действительно, на границе «запрещенной» области волновая функция имеет ненулевое значение, и оно не может скачком обратиться в нуль в запрещенной области.

Рассмотрим подробнее модель прямоугольной ямы. Такая модель непосредственно используется как простейшая модель свободных электроновв металле. Среди многих задач с прямоугольными ямами простейшей является задача о частице в потенци-альном ящике. В этом случае потенциальная энергия равна нулю на некотором отрезке оси x от 0 до 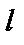, и скачком обращается в бесконечность на концах этого отрезка (рис.2.5). Частица оказывается запертой на этом отрезке и не может выйти за его пределы. Такой характер потенциальной энергии описывается формулой:

Рис.2.5

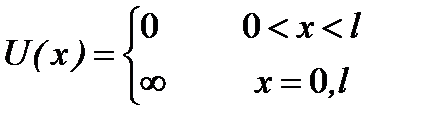. (2.21)

Найдем граничные условия для волновой функции. Обозначая , из (2.20) получим:

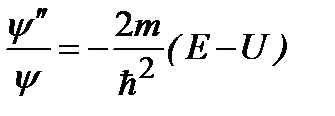. (2.21a)

При 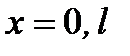правая часть в (2.21а) согласно (2.21) обращается в бесконечность. Так как волновая функция и ее производные не могут принимать бесконечно большие значения, то в этих точках должна обращаться в нуль волновая функция:

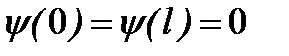. (2.22)

Таким образом, на всем участке кроме его концов волновая функция удовлетворяет уравнению:

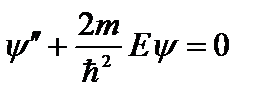. (2.23)

Это уравнение с граничными условиями (2.22) представляет задачу на собственные значения. Его общее решение

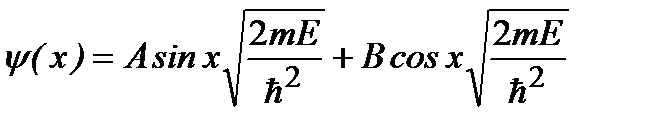, (2.24)

где A,B – постоянные, определяемые граничными условиями и условием нормировки. Из граничных условий (2.22) следует: 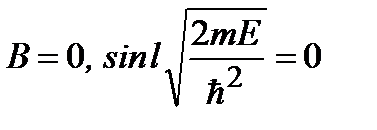. Таким образом,

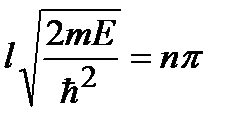, (2.24a)

где число 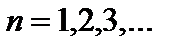Значение n = 0 исключается, так как в этом случае при всех x, т.е. такое состояние не реализуется. Из (2.24a) следует, что решение уравнения (2.23) возможно не при любых значениях энергии, а лишь при вполне определенных дискретных значениях:

. (2.25)

Таким образом, частица в потенциальном ящике обладает дискретным набором состояний с энергиями (2.25). Однако эта дискретность состояний для электрона существенна только в случае ящика атомных масштабов. Действительно, рассмотрим разность между соседними уровнями энергии:

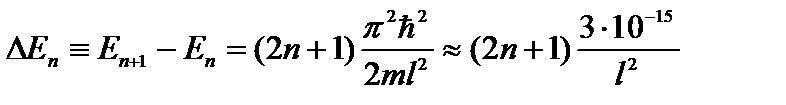эВ. (2.26)

Если l=1 см, то

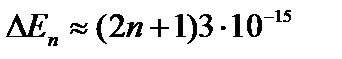эВ. (2.26а)

Этот интервал настолько мал, что практически энергетический спектр электрона в таком ящике является квазинепрерывным. Если же 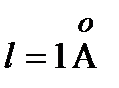, то

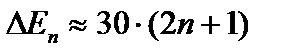эВ. (2.26б)

Этот интервал уже сравним с самими значениями энергии электрона в атоме, и даже превосходит их.

Нахождение собственных значений является лишь частью общей задачи (2.22), (2.23). Необходимо еще найти собственные функции. Согласно (2.24), (2.24а) собственные функции c cобственными значениями энергии (2.25) определяются формулой

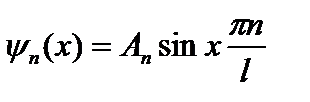. (2.27)

Эти функции образуют ортонормированную систему, т.е. они удовлетворяют условию (2.14):

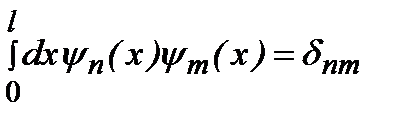, (2.28)

Постоянная 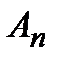определяется из условия нормировки:

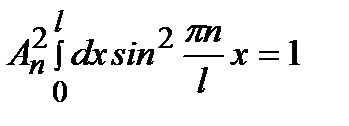. (2.28a)

Отсюда 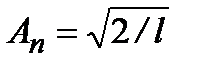. Таким образом, ортонормированная система собственных функций частицы в потенциальном ящике описывается формулой:

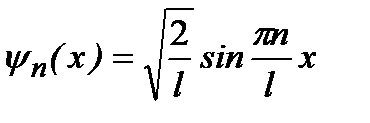. (2.29)

Собственные функции с энергией 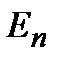равны 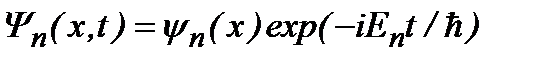. По общим правилам, выражение

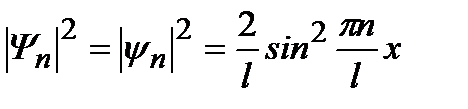(2.30)

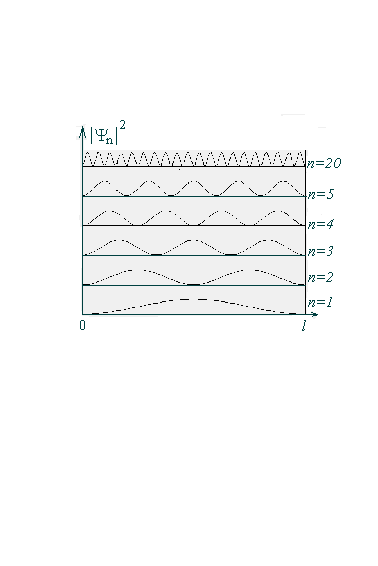
определяет плотность вероятности того, что частица находится в интервале от x до x + dx. На рис.2.6 изображена плотность вероятности для разных состояний. Эти зависимости не имеют ничего общего с результатом аналогичной классической задачи, в которой плотность вероятности постоянна и равна 1/l. Однако с увеличением номера n число максимумов возрастает, и они располагаются все ближе друг к другу. При достаточно больших значениях энергии максимумы сближаются настолько, что образуют почти непрерывную прямую, близкую к прямой для

Рис.2.6 плотности вероятности в классическом случае. В этом состоит

принцип соответствия в рассматриваемой задаче.

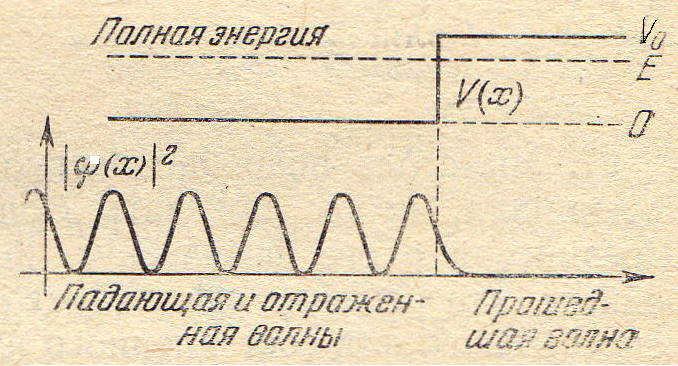5. Отметим некоторые особенности «барьерных» задач (рис.2.4). Допустим, что частица падает на барьер слева направо с энергией (рис.2.4а). Тогда при достижении точки 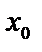(точки поворота) классическая частица полностью отразилась бы от барьера. Для нее область 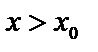«запрещена». Для квантовой частицы, однако, имеется отличная от нуля вероятность обнару-жить ее и в «запрещенной» области (рис.2.7). Этот эффект анало-гичен известному в оптике явлению полного внутреннего отра-жениясвета на границе раздела двух разных сред. С увеличением высоты потенциального барьера область «просачивания» частицы уменьшается и при 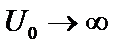стремится к нулю. В этом случае волновая Рис.2.7

функция при 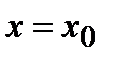обращается в нуль. Если 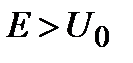, то классическая

частица проходит такой барьер без всякого отражения. В квантовом же случае наряду с проходящей волной де Бройля имеется также отраженная от барьера волна, и можно вычислить соответствующий коэффициент отражения. Если ширина барьера конечна (рис.2.4б) и энергия падающей слева частицы меньше высоты барьера, то возникает чисто квантовый эффект просачивания частицы сквозь барьер – туннельный эффект. Этот эффект объясняет многие физические явления, такие как контактная разность потенциалов, холодная эмиссия электронов из металлов, альфа–распад и др.

При рассмотрении барьерных задач важную роль играют коэффициент отраженияот барьера и коэффициент прозрачностибарьера. Коэффициент отражения определяется как отношение плотности потока отраженной волны к плотности потока падающей волны:

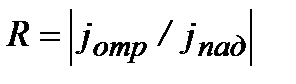. (2.32)

Коэффициент прозрачности барьера определяется как отношение плотности потока волны, прошедшей через барьер, к плотности потока падающей волны:

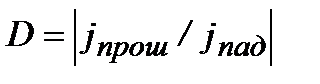. (2.32а)

Введенные коэффициенты удовлетворяют очевидному условию:

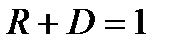. (2.33)

Плотность потока частиц определяется общей формулой (2.13).