Расчет характеристик влияния электрического поля на магнитное экранирование ядер в молекулярных системах с осевой симметрией.
Известно, что электрические поля оказывают заметное влияние на константу ядерного магнитного экранирования s , которое обнаруживается в сдвиге резонансной частоты ядра. В основе такой интерпретации лежит зависимость, полученная Бакингэмом [1], который рассмотрел влияние полярной группы в молекуле на изменение s протона в связи С-Н. На основе качественных рассуждений было установлено, что электрическое поле E , обусловленное влиянием полярных групп либо в пределах самой молекулы, либо от соседних молекул растворителя, ведет к химическим сдвигам 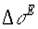 протона в связи С-Н, равным
протона в связи С-Н, равным
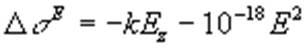 (1)
(1)
где 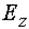 - проекция вектора E на направление связи, а k, для протона, имеет порядок (2-4)*10-12 (эл.-стат. ед.)-1. Для перехода к атомным единицам необходимо умножить k на 17.153*1012. Таким образом, электрическое поле, направленное от атома С к атому Н, сдвигает электроны связи от экранируемого атома Н к С, что приводит к сдвигу сигнала протона в сторону меньших значений магнитного поля.
- проекция вектора E на направление связи, а k, для протона, имеет порядок (2-4)*10-12 (эл.-стат. ед.)-1. Для перехода к атомным единицам необходимо умножить k на 17.153*1012. Таким образом, электрическое поле, направленное от атома С к атому Н, сдвигает электроны связи от экранируемого атома Н к С, что приводит к сдвигу сигнала протона в сторону меньших значений магнитного поля.
Формула (1) нашла широкое применение при интерпретации спектров ЯМР, при этом квадратичные вклады в большинстве случаев малы. Формализм, связанный с учетом влияния на s электрических полей и магнитно-анизотропных эффектов, позволяет объяснить химические сдвиги в таких сложных молекулярных системах, как белковые молекулы [2].
К примеру построен алгоритм вычислений линейной по электрическому полю поправки к s произвольного ядра в связях X-Y, создаваемой полярной группой молекулы, используя вариационный метод [3,4] в сочетании с неэмпирическими волновыми функциями, невозмущенными магнитным полем.
Было получено следующее выражение для линейного по полю 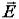 приращения к тензору s :
приращения к тензору s :
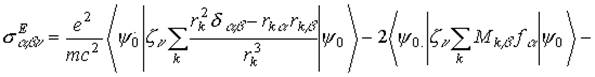
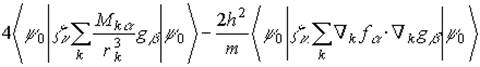 (2)
(2)
где 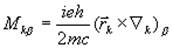 , а волновая функция, возмущенная внешним магнитным полем Н, электрическим полем Е и магнитным моментом ядра m представлена в виде
, а волновая функция, возмущенная внешним магнитным полем Н, электрическим полем Е и магнитным моментом ядра m представлена в виде
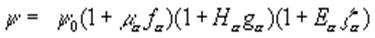 (3)
(3)
Здесь 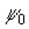 -невозмущенная волновая функция основного состояния, являющаяся решением уравнения Шредингера в отсутствие ядерного магнитного момента и внешних полей, а
-невозмущенная волновая функция основного состояния, являющаяся решением уравнения Шредингера в отсутствие ядерного магнитного момента и внешних полей, а 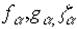 -неизвестные пробные функции от радиуса-вектора электрона
-неизвестные пробные функции от радиуса-вектора электрона 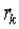 , в общем случае комплексные.
, в общем случае комплексные.
В случае осевой симметрии 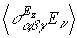 отлично от нуля, когда электрическое поле имеет ненулевую компоненту вдоль оси связи ( ось z), поэтому
отлично от нуля, когда электрическое поле имеет ненулевую компоненту вдоль оси связи ( ось z), поэтому
 (4)
(4)
Искомые поправочные функции были выбраны в виде
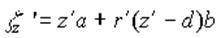 ,
, 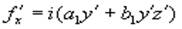 ,
, 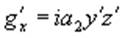 , (5)
, (5)
Здесь d выбирается так, чтобы выполнялось условие ортогональности 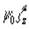 и
и 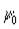 , необходимое для обеспечения инвариантности выражения поляризуемости относительно переноса начала координат. Полагая, что для искомого набора параметров компоненты тензоров поляризуемости
, необходимое для обеспечения инвариантности выражения поляризуемости относительно переноса начала координат. Полагая, что для искомого набора параметров компоненты тензоров поляризуемости 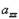 , магнитной восприимчивости
, магнитной восприимчивости 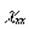 и магнитного экранирования
и магнитного экранирования 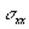 имеют экстремум, решаем следующую систему уравнений
имеют экстремум, решаем следующую систему уравнений
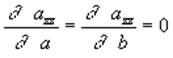 ;
; 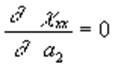 ;
; 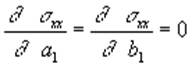
Подставляя поправочные функции (5) в формулу (2), получим следующие выражения для диамагнитного 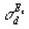 и парамагнитного
и парамагнитного 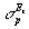 вкладов в
вкладов в 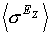 :
:
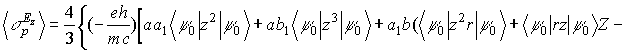
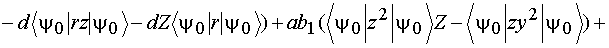
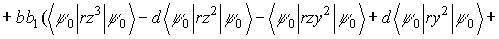
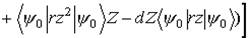 (6)
(6)
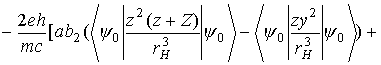
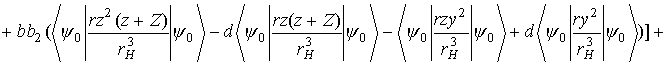
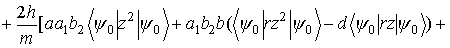
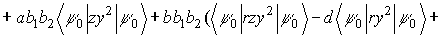
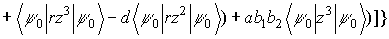 (7)
(7)
Полученные формулы позволяют производить прямой неитерационный расчет характеристик влияния электрического поля на магнитное экранирование ядер в молекулярных системах с осевой симметрией.
Был разработан алгоритм и создана программа на языке FORTRAN для персонального компьютера. Часть интегралов, содержащихся в формулах (6-7) , была взята в аналитическом виде. Наиболее сложные интегралы решались численным методом, что позволило использовать слейтеровские волновые функции для описания экранируемой связи. При этом применили преобразование канонических молекулярных орбиталей (МО) к локализованным МО методом Бойса.
Для проверки эффективности разработанного алгоритма расчета 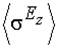 на ядрах 1Н, 13C, 19F были проведены тестовые вычисления отдельных связей с использованием стандартной функции Ричардсона. Результаты расчетов показаны в таблицах 1. и 2.
на ядрах 1Н, 13C, 19F были проведены тестовые вычисления отдельных связей с использованием стандартной функции Ричардсона. Результаты расчетов показаны в таблицах 1. и 2.
Таблица 1.Значения параметров поправочных функций для экранирования 1H в связях С-Н.
| d | a | b | a1 | b1 | b2 | |
| sp3 | 0.114 | -1.467 | -0.328 | 0.259 | -0.029 | 0.148 |
| sp2 | 0.022 | -1.276 | -0.272 | 0.265 | -0.042 | 0.097 |
| sp | 0.025 | -1.265 | -0.136 | 0.267 | -0.040 | 0.030 |
| (sp3) [4] | 0.086 | -1.178 | -0.270 | 0.244 | -0.037 | 0.086 |
Таблица 2.Значения поправок к магнитному экранированию 13С в связях С-Н, C-C и 1Н в связи Н-Н, обусловленных влиянием электрического поля
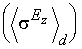
| 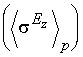
| 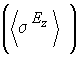
| 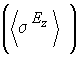
| |
| H-H | 3.226 | 0.635 | 3.861 | 3.1 [5] |
| C*-H | 25.830 | 6.845 | 32.675 | 30 [6] |
| C-C | 44.071 | 10.247 | 54.318 | 51 [6] |
Сравнение полученных результатов с экспериментальными данными подтверждает работоспособность разработанного алгоритма как для расчета ядер 1H ,так и ядер 13C.Были проведены также расчеты 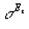 ряда молекул, для которых имеются достоверные ЯМР экспериментальные результаты. При этом использовались волновые функции молекул, рассчитанные в базисе STO-3G и локализованные методом Бойса. В таблице 3 приведены результаты расчетов диамагнитного, парамагнитного и суммарного вкладов в линейную по электрическому полю вариацию константы экранирования в связях C-H, C-C, C-N, C-O, C-F, которые сравниваются литературными данными. В [6] результаты получены на основе эмпирических оценок, с использованием поляризуемости связи. Результаты работы [7] получены методом конечных возмущений в сочетании с неэмпирическим методом самосогласованного поля.
ряда молекул, для которых имеются достоверные ЯМР экспериментальные результаты. При этом использовались волновые функции молекул, рассчитанные в базисе STO-3G и локализованные методом Бойса. В таблице 3 приведены результаты расчетов диамагнитного, парамагнитного и суммарного вкладов в линейную по электрическому полю вариацию константы экранирования в связях C-H, C-C, C-N, C-O, C-F, которые сравниваются литературными данными. В [6] результаты получены на основе эмпирических оценок, с использованием поляризуемости связи. Результаты работы [7] получены методом конечных возмущений в сочетании с неэмпирическим методом самосогласованного поля.
Для определения эффективного значения напряженности электрического поля, создаваемого полярными группами внутри молекулы, мы использовали распределение электростатического потенциала в молекуле, получаемое при расчете конкретных МО. На рис. 1 показано сечение эквипотенциальных поверхностей плоскостью, проходящей через Н-С-Н фрагмент молекулы CH4
Таблица 3.Диамагнитный, 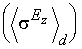 парамагнитный
парамагнитный 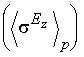 и полный
и полный 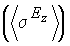 вклады в линейную по электрическому полю вариацию константы экранирования для связей в изученных молекулах.
вклады в линейную по электрическому полю вариацию константы экранирования для связей в изученных молекулах.
| Молекула | Связь | 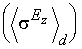
| 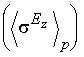
| 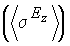
| 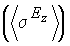 [6,7] [6,7]
|
| CH4 | C-H* | 3.22 | 0.63 | 3.85 | |
| C-H* | 5.84 | 0.93 | 6.77 | ||
| C*-H | 20.24 | 5.42 | 25.66 | 30.0 [6] | |
| C-H* | 6.11 | 0.38 | 6.49 | ||
| CH3F | C*-H | 24.29 | 7.25 | 31.81 | |
| C*-F | 51.37 | 16.08 | 67.45 | ||
| C-F* | 82.17 | 19.33 | 101.5 | (Cl=120.0 Br=82.0) [6] | |
| CH3OH | C-H* | 5.96 | 0.75 | 6.71 | |
| C-O* | 61.52 | 15.04 | 76.56 | ||
| C*-H | 22.92 | 6.18 | 29.80 | ||
| CH3-CH3 | C-H* | 4.77 | 0.51 | 5.28 | |
| C*-H | 20.95 | 6.23 | 27.18 | ||
| C-C* | 44.97 | 10.22 | 55.19 | 51.0 [7] | |
| C-H* | 5.36 | 1.19 | 6.55 | ||
| CH3COH | C*-H | 22.71 | 4.45 | 27.16 | |
| C*-O | 58.40 | 16.01 | 74.41 | ||
| C-H* | 5.02 | 0.98 | 6.00 | ||
| CH3NH2 | C*-H | 22.33 | 1.59 | 23.92 | |
| C*-N | 36.21 | 7.5 | 43.71 | 45.0 [7] | |
| C-H* | 5.68 | 1.46 | 7.14 | ||
| CH3NO2 | C*-H | 23.94 | 7.20 | 31.14 | |
| C*-N | 40.69 | 8.3 | 48.99 |
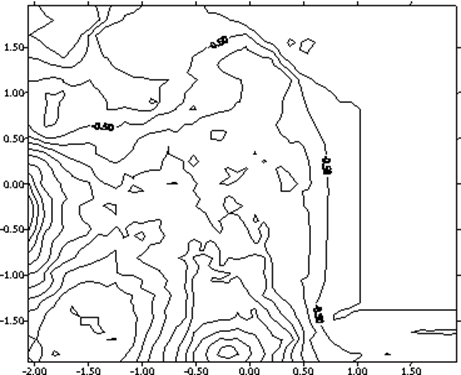


 Рис. 1.
Рис. 1.
Экранирование.
Экранирование – локализация электромагнитной энергии в определенном пространстве за счет ограничения распространения ее всеми возможными способами.
Полное экранирование может быть получено только при подавлении всех видов электромагнитных связей (электрическое поле, магнитное поле, электромагнитное поле) , но требования к эффективности экранирования в ряде случаев могут быть снижены. В этих случаях задачей экрана может быть ослабление того или иного вида связи.
Дата добавления: 2016-01-07; просмотров: 1346;
