Математические алгоритмы применения фильтров к изображению
В компьютерной графике цифровое изображение представляет собой набор чисел и, меняя эти числа определенным образом, можно прийти к удивительным и полезным спецэффектам. Автор ограничен рамками книги и не имеет возможности показать идеологию работы всех фильтров Photoshop. Поэтому, для иллюстрации сказанного, ограничимся рассмотрением алгоритмов (принципов) работы только двух фильтров:
- Blur (Размытие). Процесс размывания изображения сводится к перераспределению цветов изображения, уменьшению его резкости и смягчению цветовых границ;
- Sharpen (Резкость). При увеличении резкости изображения, наоборот, подчеркиваются различия между цветами смежных пикселей, нечеткость изображения уходит, выделяются ранее незаметные детали.
Если работу фильтра рассматривать, как компьютерную программу, то алгоритм работы каждого из перечисленных фильтров кроется в матрице чисел 3 3, которая содержит три строки по три числа в каждой. Условное графическое изображение такой матрицы приведено на рис. 5.27.

Рис. 5.27. Условная матрица чисел 3x3
Итак, предположим, что в центре этой матрицы находится пиксель, который будет преобразован фильтром. Тогда его новое значение будет выстроено в соответствии с его цветом и цветом окружающих его восьми пикселей, который подвергаются фильтрации (умножению и сложению) их цветовых значений. Поскольку фильтрация происходит для каждого пикселя оригинального изображения, то процесс преобразования оригинального изображения фильтром требует времени и значительных ресурсов ПК.
Для фильтра Blur (Размытие) каждый из коэффициентов фильтрации меньше 1, а их сумма составляет 1. Это означает, что каждый пиксель поглощает что-то из цветов соседей, но полная яркость изображения остается неизменной (если сумма коэффициентов больше 1, яркость увеличится; если меньше 1, яркость уменьшится). При подготовке к размыванию цифровое изображение считывается в память компьютера в виде красного, зеленого и синего компонентов цвета каждого пикселя. Ядро размывания размером 3x3 применяется к красному, зеленому и синему компонентам цвета каждого пикселя изображения. Значение цвета пикселя, который, находится в центре матрицы, вычисляется умножением соответствующего весового коэффициента на соответствующее ему значения цвета в изображении с последующим суммированием результатов. Итоговое изображение получается размытым по сравнению с оригиналом потому, что цвет каждого пикселя выравнивался (усреднялся) благодаря влиянию соседей. Степень размывания можно увеличить разными способами, например, изменением размера ядра установкой параметра Радиус (Radius) размытия - рис. 5.28.
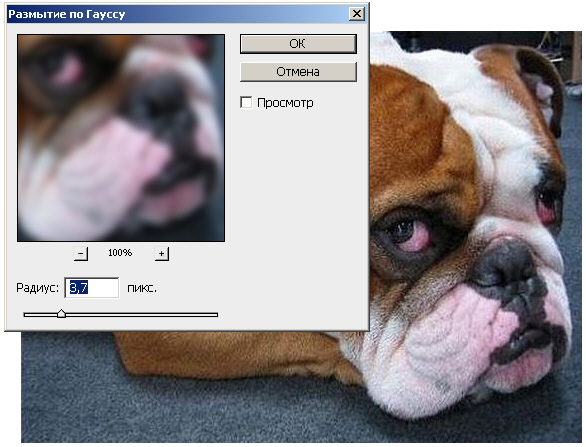
Рис. 5.28. Размытие по Гауссу изменением радиуса ядра матрицы
Для фильтра Sharpen (Резкость) центральный коэффициент больше 1, а окружающие его значения являются отрицательными числами, сумма которых на единицу меньше центрального коэффициента. Таким образом, достигается увеличение существующего контраста между цветом пикселя и цветами его соседей. В этом случае при преобразовании изображения меняется четкость изображения: она не уменьшается, как при размытии, а наоборот - увеличивается. При обработке каждого пикселя в изображении с помощью фильтра Sharpen (Резкость) также используется ядро резкости размером 3x3. Красная, зеленая и синяя цветовые составляющие обрабатываются отдельно и позже объединяются, чтобы сформировать 24-битное значение цвета. Отрицательные коэффициенты вокруг центра ядра увеличивают контраст между центральным пикселем и соседями. Зону резкости изображения можно менять разными способами, например, изменением размера ядра посредством перемены параметра Радиус (Radius) - рис. 5.29.
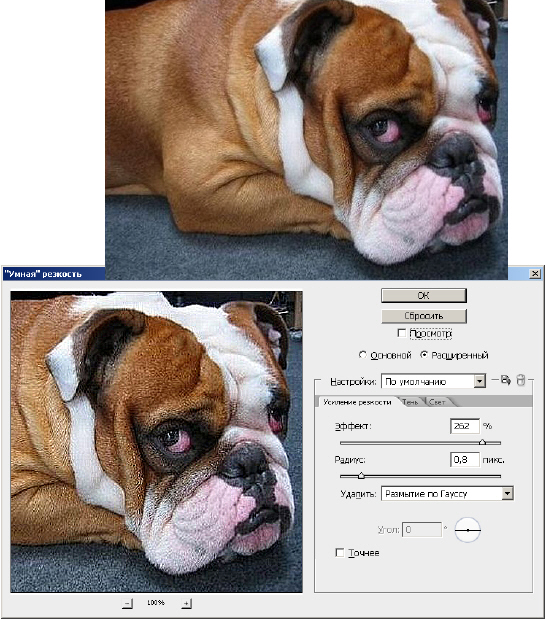
Рис. 5.29. Увеличение резкости изображения фильтром Умная резкость
После применения этого фильтра изображение становится более четким по сравнению с оригиналом. Процесс увеличения резкости произошел из-за программного повышения контраста между пикселями. При повторной обработке изображения тем же фильтром четкость может увеличиться еще больше.
Примечание
Обратите внимание, что сильное увеличение резкости увеличивает "зернистость" изображения.
Дата добавления: 2016-01-07; просмотров: 1069;
