Долговечность железобетонной колонны при наличии ползучести бетона
Как и ранее рассмотрим на примере железобетонной колонны (см. рис.9.6.1.) метод определения ее ресурса.
Пусть как и ранее:
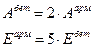 .
Примем, что арматура чисто упругий элемент, а бетон является вязким, то есть ползет (см. раздел 8.1) .
Примем, что арматура чисто упругий элемент, а бетон является вязким, то есть ползет (см. раздел 8.1)
|  рис. 9.6.1.
рис. 9.6.1.
|
по закону:
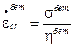 (9.6.1.1)
(9.6.1.1)
Упругая часть деформации определяется по закону Гука:

Найдемсначаланапряжения в бетоне 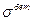 и в арматуре
и в арматуре 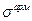 , а затем из условия прочности определим время, до которого оно будет выполняться.
, а затем из условия прочности определим время, до которого оно будет выполняться.
Поскольку ползучесть происходит во времени, то напряжения и деформации тоже являются функциями времени t:
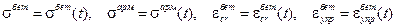 .
.
Часть силы F распределяется на бетон, часть на арматуру:
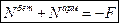 (9.6.1.4)
(9.6.1.4)
Решений бесконечное множество, для выбора из них соответствующего задаче нужно привлекать дополнительное условие. Как и ранее имеем:
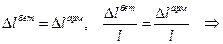
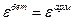 (9.6.1.5)
(9.6.1.5)
В (9.6.1.5) подставим нижеследующие соотношения:
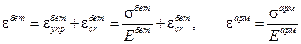 .
.
Продифференцируем условие совместности (9.6.1.5) по времени:
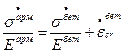 .
.
Подставим сюда 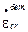 в соответствии с законом ползучести (9.6.1.1):
в соответствии с законом ползучести (9.6.1.1):
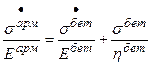 (9.6.1.6)
(9.6.1.6)
Исключим отсюда 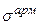 . Для этого используем связь усилий и напряжений:
. Для этого используем связь усилий и напряжений:
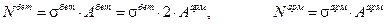
Тогда из (9.6.1.4) вытекает, что:
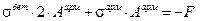 .
.
Деля на площадь арматуры, получим:
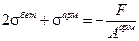 . (9.6.1.7)
. (9.6.1.7)
Дифференцируя это соотношение по t и получим:
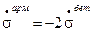
Теперь подставим это в (9.6.1.6):
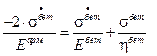 .
.
Получили дифференциальное уравнение относительно неизвестной 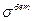 . Умножая его на
. Умножая его на 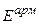 и деля на 7 получим:
и деля на 7 получим:
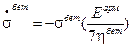 .
.
Решение его известно и имеет вид:
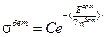 (9.6.1.8)
(9.6.1.8)
Константу С находят из каких-либо известных условий, а именно нам известны 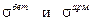 в начальный момент времени (см. задачу 9.1), т.е. при
в начальный момент времени (см. задачу 9.1), т.е. при 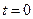 можно записать:
можно записать:
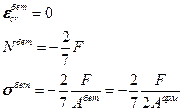
Подставим в (9.6.1.8):
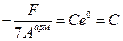 .
.
Полученное С подставляем в (9.6.7). Учитывая, что 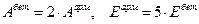 получаем:
получаем:
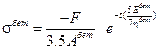 .
.
Анализ решения:
Из последнего выражения видно, что при больших 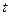 напряжение
напряжение 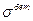 становится все меньше и меньше, т.е. стремится к нулю.
становится все меньше и меньше, т.е. стремится к нулю.
Таким образом, с течением времени бетон разгружается.
Определение: такое явление называется релаксацией или отдыхом материала.
Арматура, напротив, в это время догружается, значит при больших 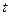 получим:
получим: 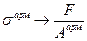 , т.е. вся нагрузка будет приходиться на арматуру.
, т.е. вся нагрузка будет приходиться на арматуру.
Проведем теперь расчет на долговечность. Под термином долговечность будем понимать время t*, в течение которого удовлетворяются условия прочности. Имеем:
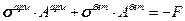
Поделим на 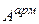 , тогда получим:
, тогда получим:
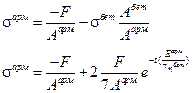
Пусть в момент 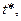 в арматуре напряжение
в арматуре напряжение 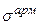 достигает допустимого напряжения (ниже учтено, что при сжатии напряжения отрицательны):
достигает допустимого напряжения (ниже учтено, что при сжатии напряжения отрицательны):
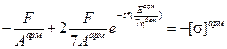 .
.
Перенося первое слагаемое вправо и логарифмируя это уравнение, получим:
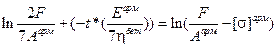 .
.
Отсюда:
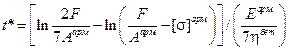 .
.
Это и есть время, в течение которого можно безопасно эксплуатировать колонну (можно сказать, что это ресурс колонны).
Дата добавления: 2015-11-28; просмотров: 903;
