Закон парности касательных напряжений. Вырежем из тела малый элемент (рис.6.3.)

Вырежем из тела малый элемент (рис.6.3.). Со стороны соседних элементов на него кроме растягивающих напряжений действуют и касательные напряжения (рис.6.4.). Рассмотрим случай, когда растягивающих напряжений нет. Поскольку все тело находится в покое, то и любая его часть, в том числе рассматриваемый малый параллелепипед также находится в покое.

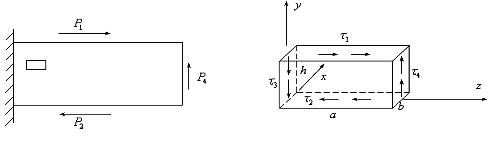
Рис.6.3. Рис.6.4.

Запишем для него уравнения равновесия:

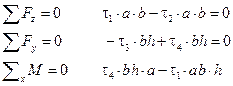
Отсюда вытекает

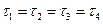
Закон парности можно сформулировать следующим образом.

Если на грани элемента тела возникает напряжение t, то на других трех гранях также возникает такое же напряжение t. При этом они сходятся к ребру или расходятся от ребра.

Примечание. Здесь мы рассмотрели случай отсутствия нормальных напряжений. Но этот закон имеет место и при их наличии. Для доказательства этого надо использовать следующие соображения.

Если вертикальные грани имеют бесконечно малый размер h по сравнению с горизонтальным, то нормальные напряжения не будут давать вклад в первое уравнение равновесия. Аналогично для второго уравнения. Для третьего уравнения можно выбрать ось х, проходящей через центр параллелепипеда.

Деформации

Деформирование – это процесс изменения размеров тела.

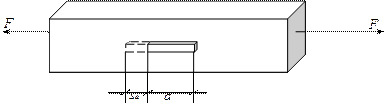Деформация – это число, которое характеризует изменение размера тела.

Рассмотрим растяжение бруса. В результате деформирования малый элемент получит абсолютное удлинение на величину .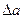

Определение: Относительным удлинением (синоним - линейная деформация) называется величина:

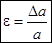
Правило знаков. Согласно определению понятия «приращение» запишем 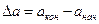. Отсюда следует, что если элемент удлиняется, то 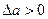, а значит 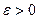, если элемент укорачивается то 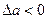, и значит .

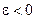Примечание: Часто понятия растяжение и удлинение используют как синонимы. Однако это не так, понятие растяжение (сжатие) - это силовая характеристика, удлинение (укорочение) – геометрическая. Иногда бывает и так, что элемент сжат, но не деформируется (например, при нагреве элемента, зажатого в жесткой обойме) или даже удлиняется.

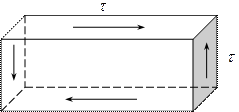
Рассмотрим теперь другой вид деформирования элемента тела под действием касательных воздействий.

Под действием 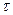прямой параллелепипед превращается в косоугольный.

Угол 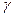называется деформацией сдвига (синонимы: угол сдвига, сдвиг).