Принципы квантовой механики

I.Принцип дополнительностисформулирован Н. Бором (1927 г). Согласно этому принципу наличие информации об одних физических величинах, описывающих микрообъект (элементарная частица, атом, молекула) неизбежно связано с потерей информации о других величинах, дополняющих первые. Такими величинами, например, являются координата частицы и ее скорость (или импульс).

Принцип дополнительности Бор рассматривал как методологический принцип, в широкой трактовке этот принцип означает, что описывать физический объект, относящийся к микромиру, нужно во взаимоисключающих, дополнительных системах, например, одновременно и как волну, и как частицу.

Посмотрим, говорил Бор, с этой точки зрения на то, сводятся ли биологические закономерности к физико-химическим процессам?

Нет, закономерности живой материи, хотя и определяются законами физики и химии, но не сводятся к ним. Бор обосновывает мысль, что два подхода – биологический и физико-химический – дополнительны.

Аналогично можно говорить о дополнительности анализа и синтеза, научного и иррационального и др.

В физике количественным воплощениям общего принципа дополнительности Бора явилось соотношение неопределенностей Гейзенберга.

II.Принцип неопределенности (соотношение неопределенностей Гейзенберга, открыт в 1927 г.).

Объект микромира невозможно одновременно с заданной точностью характеризовать координатой и импульсом. В классической механике частица движется по определенной траектории и в любой момент точно фиксированы ее координата и импульс. Согласно соотношению неопределенности Гейзенберга частица не может иметь одновременно и точно определенную координату (х, у, z) и определенную соответствующую проекцию импульса (Р_х, Р_у, Р_z), причем неопределенность этих величин удовлетворяют условиям:

Dх ×DР_х ³ h/2p, Dу ×DР_у ³ h/2p, Dz ×DР_z ³ h/2p,

где h – постоянная Планка; Dх, Dy, Dz – неопределенности координат; DР_х, DР_y, DР_z – неопределенности проекций импульса.

Если выражение DР_х заменить на DР_х = Dv_x×m, то

,

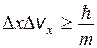т.е. чем больше масса частицы, тем меньше неопределенности (Dх; Dv_x) ее координаты и скорости и тем с большей точностью можно применить к этой частице понятие траектории.

Например, для пылинки массой m = 10^–13 кг и линейными размерами l = 10^–6 м, координата которой определена с точностью до 1/100 ее размера (Dх = 10^–8 м), неопределенность скорости Dv:

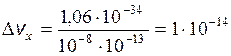м/с (h = 1,06×10^–34 Дж×с),

т.е. х и v определяются точно.

Нерелятивистское уравнение квантовой механики Шредингера играет в этой науке такую же роль, какую II закон Ньютона играет в классической механике (который является уравнением движения макрообъекта).

Релятивистское уравнение квантовой механики написал Поль Дирак.