Максимизация прибыли в условиях совершенной (чистой) конкурентной
Модельсовершенно конкурентной фирмы показывает, что прибыль максимизируется при соблюдении двух критериев:
1) сравнения общего дохода и совокупных издержек;
2) сравнения предельных издержек и предельного дохода.
| Максимизация прибыли в условиях совершенной конкуренции | |
| основная задача конкурентной фирмы | |
| выбор оптимального объема производства для достижения максимизации прибыли или минимизации убытков | |
| пути решения | |
| сопоставлениевалового (общего) доходаиваловых (общих) издержек | сопоставлениепредельного доходаипредельных издержек |
| особенности совершенной конкуренции | |
| предельный доход, средний доход и цена совпадают; во всех рыночных структурах максимизация прибыли происходит на основе равенства предельных издержек и предельного дохода, но только в условиях совершенной конкуренции соблюдается равенство предельных издержек, предельного дохода и цены (МС=MR=Р) |
Рис.9.3. Максимизация прибыли в условиях совершенной конкуренции
| Определение оптимального объема производства на основе сопоставления валового дохода и валовых издержек для совершенно конкурентной фирмы | |
| максимизации прибыли предполагает | графическое изображение |
| объем производства, при котором валовый доход превышает валовые издержки на максимальную величину |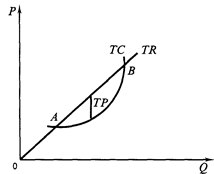 
|
| · разница по высоте между кривыми валового дохода и валовых издержек – это прибыль при любом объеме выпуска; · точки пересечения кривых валового дохода и валовых издержек – это точки критического объема производства. |
Рис.9.4. Проверка прибыльностью для выбора оптимального объема производства
для фирмы в условиях совершенной конкуренции
| Предельный анализ максимизации прибыли в условиях совершенной конкуренции | ||
| максимизация прибыли предполагает | ||
| сопоставление сумм, которые каждая дополнительная единица продукции будет добавлять к валовому доходу и совокупным издержкам | ||
| для совершенно конкурентной фирмы предельный доход MR и цена товара P совпадают | ||
| условие максимизации прибыли при совершенной конкуренции | ||
| MR=MC=P | ||
| три состояния краткосрочного равновесия отдельной фирмы | ||
| фирма несет убытки (MC=MR=P2 и Р2<АТС), при этом фирма продолжает производство если Р1>АVС При Р=min AVC фирма прекратит производство | фирма лишь покрывает свои издержки (MC=MR=P3 и Р3=АТС) При Р=min AТC прибыль фирмы равна нулю | фирма работает с экономической прибылью (MC=MR=P1 и Р1>АТС) |
| графически |
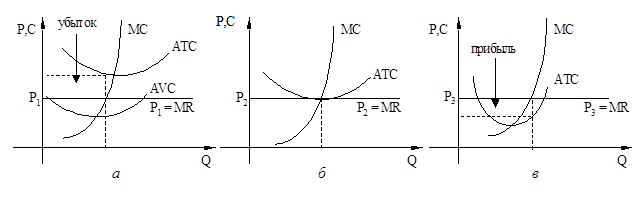Рис.9.5. Различные варианты краткосрочного равновесия:
а – фирма несет убытки;
б – нулевая экономически прибыль;
в – фирма получает экономическую прибыль
| Равновесие фирмы и отрасли в долгосрочном периоде | |||
| условия | |||
| существующие фирмы ведут себя максимально эффективно при имеющихся у них предприятиях и технологии, т.е. МС=Р и отдельная фирма не будет изменять объем выпускаемой продукции | не существует стимулов для новых фирм вступать на данный рынок, т.е. старые фирмы не получают никакой экономической прибыли на имеющихся у них предприятиях, которая могла бы привлечь их конкурентов: Р=АТС (предложение на рынке не меняется) | существующие фирмы не в состоянии увеличивать прибыль, строя новые предприятия других размеров, т.е. действующие фирмы находятся в точке минимума долгосрочной кривой издержек: Р = LRAТС | |
| равновесие фирмы в долгосрочном периоде | равновесие отрасли в долгосрочном периоде | ||
| достигается при выпуске такого объема продукции, при котором средних валовых издержек минимальныпри заданном уровне развития технологии и цен на производственные факторы | Когда все фирмы функционируют в точке минимума своих долгосрочных кривых средних издержек и при этом цена лишь покрывает эти издержки, вся отрасль находится в состоянии долгосрочного равновесия | ||
| это | так как | ||
| минимально эффективный размер фирмы | совокупное предложение и рыночная цена остаются неизменными и никому из участников рынка нет смысла менять свое поведение | ||
| графическое изображение | |||
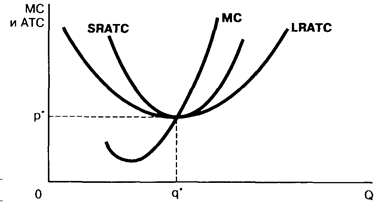
Рис. 9.6. Равновесие фирмы в долгосрочном периоде
Дата добавления: 2015-11-28; просмотров: 1253;