Конвекция в мантии Земли

Важнейшим процессом, обусловливающим динамику мантии и, в ко­нечном счете, и земной коры, является конвекция, прежде всего тепловая (рис. 16 на цветной вклейке). Если бы внутреннее тепло, накапливающе­еся в Земле в результате действия описанных факторов (см. 18.1), посту­пало к поверхности лишь путем обычной теплопроводности, т. е. кондуктивного теплопереноса, Земля неминуемо довольно быстро разогрелась бы до полного плавления. Это было ясно уже более трех десятилетий тому назад, когда величина теплового потока, достигающего поверх­ности Земли, оценивалась гораздо ниже, чем в настоящее время, после открытия мощного тепловыделения в рифтовых зонах срединно-океанских хребтов. Именно то обстоятельство, что в мантии Земли теплоперенос осуществляется не только кондуктивным, но и конвективным путем, гарантирует нашу планету от перегрева. Но непосредственное подтверждение реальности мантийной конвекции поступило лишь в последние годы, когда сейсмотомографией были получены данные, сви­детельствующие о существовании в мантии на одних и тех же уровнях более разогретых участков (соответственно менее плотных, с меньшими скоростями распространения сейсмических волн) и менее разогретых, уплотненных, высокоскоростных участков.

Термин «конвекция» в переводе с латинского означает «доставка», при этом первоначально имелась в виду лишь доставка тепла. Частным случаем конвекции является адвекция, процесс которой носит затухаю­щий характер вследствие исчерпания породившего его источника возму­щения. В расширенном смысле конвекция может быть не только тепловой, но и химической (концентрационной), когда насыщенные не­которым веществом элементарные объемы перемещаются в направлении меньшей концентрации этого вещества, где отлагают его избыток.

По другому признаку (не что, а как доставляется) конвекция под­разделяется на вынужденную и свободную. При вынужденной тепловой конвекции движение теплоносителя обусловлено внешней причиной, например при нагнетании горячей воды в жилое помещение посредством насоса. При свободной тепловой конвекции ее причиной является тепло­вое расширение частиц теплоносителя, сопровождаемое уменьшением их плотности, и их перемещение под действием силового поля в направ­лении уменьшения потенциала последнего. В качестве силового поля обычно выступает поле силы тяжести, поэтому такая конвекция называ­ется тепловой гравитационной, или соответственно химической грави­тационной. Она может продолжаться сколько угодно долго, пока суще­ствует градиент температуры или концентрации. Но при вещественной (плотностной) конвекции, т. е. при всплывании легкого вещества вверх и погружении тяжелого вниз, процесс продолжается лишь до окончания их перераспределения. Это и есть собственно адвекция, наблюдаемая, в частности, при образовании соляных куполов. Вообще деформации, связанные с инверсией плотностей в коре и мантии и упоминавшиеся выше, служат проявлением свободной конвекции. Необходимо, однако, заметить, что сама по себе инверсия плотностей, т. е. расположение более легких масс под более тяжелыми, не может привести к зарождению кон­вективного течения, если поверхность раздела этих масс горизонтальна, ибо в этом случае горизонтальный градиент литостатического давления на нижнюю толщу равен нулю. Положение изменится, если на этой по­верхности возникнут неровности, даже очень слабые. Положительные неровности приведут к образованию выступов легкого вещества, кото­рые затем начнут разрастаться вследствие его нагнетания, Одновремен­но произойдет погружение «антивыступов» тяжелого вещества.

В противоположность адвекции при длительном подогреве снизу го­ризонтального слоя жидкости (квазижидкости) имеет место неограни­ченная конвекция с многократным круговоротом вещества. Это как раз и происходит в мантии Земли.

Условием проявления тепловой конвекции в мантии Земли, на пер­вый взгляд весьма плотной и твердой, служит превышение критического значения числа Рэлея — критерия гравитационной устойчивости, равного

R = (Dr : r) ^. (gh : nX)

где первый множитель представляет относительную разность плотно­стей в кровле и подошве горизонтального слоя, подогреваемого снизу, т. е. степень инверсии плотности. Помимо разности температур в подо­шве и кровле слоя этот множитель зависит от коэффициента объемного теплового расширения вещества. Второй множитель включает ускорение силы тяжести g, мощность h, кинематическую вязкость слоя n и коэффи­циент температуропроводности X. Две последние величины определя­ются так:

n=h/r

Х=c/rс

где h —вязкость; c —теплопроводность; с — удельная теплоемкость.

Анализ общей системы уравнений, включающей уравнение движе­ния Навье — Стокса, общее уравнение передачи тепла и уравнение не­прерывности, выражающее закон сохранения массы в так называемом приближении Буссинеска, приводит к следующему условию устойчиво­сти горизонтального слоя, подогреваемого снизу:

R<R₁

где R₁ — первое критическое число Рэлея, имеющее порядок 10³.

Таким образом, конвекция в горизонтальном слое возникает не при любой инверсии плотности, а лишь при превышении критического зна­чения R_1.

Из формул (1)-(3) следует, что величины, стоящие в числителе кри­терия Рэлея, представляют собой факторы, способствующие возникно­вению тепловой конвекции. Это, прежде всего, степень инверсии плотно­сти (Dr / r), возрастающая с увеличением разности температур в подошве и кровле слоя и коэффициента объемного теплового расширения. Су­щественную роль играет и мощность слоя h. Будучи в третьей степени, этот показатель отражает объем конвектирующей массы и выражает тот факт, что в поле силы тяжести большие массы вещества легче поддаются конвекции, чем малые. Для геологов это чрезвычайно существенно: если бы не существовало «барьера мощности», то в конвекцию вовлекалось бы вещество любых, самых тонких слоев, что привело бы к чрезвычайно сложным внутрислойным деформациям.

В знаменателе выражения (1) находятся факторы, препятствующие конвекции. Вязкость h отражает сопротивление жидкости относитель­ным перемещением ее участков (частиц). Коэффициент температуро­проводности X определяется выражением (3), из которого видно, что его возрастанию способствует увеличение теплопроводности c и уменьшение теплоемкости единицы объема rс. В этом показателе как бы отражается конкуренция двух основных механизмов передачи тепла — кондуктивного и конвективного. Чем выше X, тем больше плотность кондуктивного теплового потока при заданном градиенте температуры. Зато чем выше rс, тем большее количество тепла переносится единицей объема при конвективном движении.

В последние десятилетия в теоретической и экспериментальной конвективной гидродинамике получен важный с точки зрения геоло­гов результат. Он заключается в том, что наряду с первым критическим значением числа Рэлея R₁ 10³ существует второе критическое значение R₂ 10⁴. В интервале R₁ < R < R₂ устойчивы стационарные движения в виде конвективных валов. При R > R₂ устойчивыми становятся трехмер­ные, в частности гексагональные, формы стационарных конвективных движений. В экспериментах над различными жидкостями установлено, что при переходе через критический рубеж R₂, (при усилении подогрева и возрастании разности температур в подошве и кровле слоя, при уве­личении мощности или уменьшении вязкости слоя) происходит пере­стройка конвективных валов в гексагональные ячейки. В случае, когда вязкость жидкости изменяется по вертикали вместе с изменением температуры, наблюдаются вариации формы гексагональ­ных ячеек. У большинства жидкостей вязкость увеличивается при пони­жении температуры, т. е. вертикальный градиент вязкости положителен (вязкость возрастает снизу вверх). При этом возникают ячейки с вос­ходящим потоком в центре и нисходящим — по краям ячейки, т. е. по периметру шестиугольника. У некоторых жидкостей и у всех газов вер­тикальный градиент вязкости при подогреве снизу отрицателен. Вслед­ствие этого в центре ячейки возникает нисходящий поток, а по перифе­рии — компенсирующий восходящий.

Переходя к геологическим аналогиям, необходимо заметить, что в областях развития метаморфических толщ довольно обычны гнейсо­вые купола и совсем не характерны мульды. По-видимому, это связано с тем, что вязкость горных пород убывает с возрастанием температуры и степени метаморфизма, т. е. в метаморфической толще имеет место положительный вертикальный градиент вязкости. Заслуживает внима­ния и приуроченность таких куполов к областям высокоградиентного андалузит-силлиманитового типа метаморфизма, где наиболее вероят­но превышение второго критического значения R₂. В более «холодных» областях преобладает линейная в плане складчатость — возможный ре­зультат конвекции в форме валов при R₁ < R < R₂.

Выделение на поверхности Земли конвективных линейных валов и гексагональных ячеек, а среди последних — ячеек с поднятием или по­гружением в центре значительно способствует углублению наших зна­ний об условиях протекания конвекции в недрах Земли.

Напомним, что мы рассматриваем свободную конвекцию. Однако последняя может иметь, если можно так выразиться, разную «степень свободы». Наибольшую «степень свободы» конвекция обнаруживает в уже упомянутом простейшем случае бесконечного горизонтального слоя, равномерно подогреваемого снизу. Никакие посторонние факторы не на­вязывают в этом случае системе форму конвективных ячеек как в плане, так и в вертикальном разрезе. Конвективные течения в достаточно мощ­ном слое принимают форму замкнутых ячей. Идеальная ячейка в разре­зе как бы вписана в квадрат, внутри которого происходит конвективное вращение. В этой ячейке расстояние между конвективными валами и компенсирующими их впадинами соизмеримо с мощностью конвектирующего слоя. Такому представлению отвечает подмеченная в геотектони­ке закономерность, заключающаяся в соизмеримости размеров структур с глубиной их заложения. Однако такие идеальные условия реализуются не всегда, «степень свободы» конвекции может снижаться в случае, если подогрев горизонтального слоя происходит не снизу, а сбоку или при ограниченной длине конвектирующего горизонтального слоя. В первом случае конвективная ячейка оказывается резко удлиненной по горизонтали, с подтоком вещества к зоне подогрева в нижней части слоя и противотоком в верхней части. Во втором случае возникает интерференция частных и общих конвективных (адвективных) движений.

К категории вынужденной конвекции относится процесс, происходящий при субдукции литосферных плит. В этом случае со стороны субдуцирующей плиты к основанию вышележащей геосферы приложено сдвиговое усилие, возбуждающее в этой геосфере горизонтальное течение в направлении субдукции (в нижней части геосферы) и компенсационный горизонтальный противоток (в верхней части геосферы). Нижний поток вызывает образование зоны горизонтального сжатия - скучивани на фронте субдукции, что мы и видим в аккреционном клине её висячего крыла, а в тылу — зоны горизонтального растяжения, что и наблюдается на внешнем, обращенном к океану склоне глубоководного желоба. В тылу верхнего потока в обстановке горизонтального растяжения формируются впадины окраинных морей. Фронтальной части этого потока соответствует зона надвигообразования на внутреннем склоне желоба (верхняя часть аккреционного клина).

Особый интерес представляют ситуации, когда имеются две геосферы, из которых нижняя более плотная и вязкая, чем верхняя, а конвекция происходит в нижней геосфере, кровля которой остается горизонтальной. В этом случае нижняя геосфера «задает» на своей верхней поверхности, являющейся одновременно подошвой верхней геосферы, горизонтальные перемещения, характерные для конвекции. В результате в верхней геосфере возникает вынужденная конвекция в виде как бы зеркального отражения конвекции в нижней геосфере, с восходящим потоком над зоной нисходящего потока в нижней геосфере и с нисходящим над зоной восходящего потока. Соответственно в этой системе состоящей из двух геосфер, возникает двухъярусная конвекция с таким расположением ячей, что вращение в них соответствует вращению шестеренок, сцепленных как по вертикали, так и по горизонтали. При этом в нижней геосфере конвекция осуществляется свободно (квадратная ячейка в вертикальном разрезе), а в верхней — горизонтальный размер ячеек навязывается конвекцией в нижней геосфере, вертикальный размер определяется мощностью верхней геосферы..

Как мы увидим в следующем разделе, описанная ситуация может иметь место в мантии Земли, где роль нижней геосферы может играть нижняя мантия, а верхней геосферы — верхняя мантия (рис. 18.2).

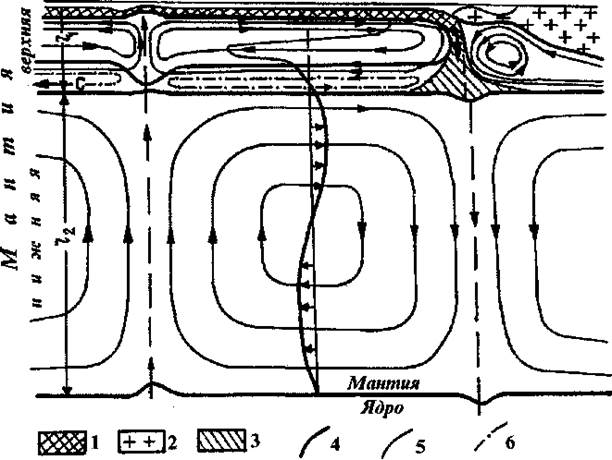
Рис. 1.Схема мантийных течений, по Н. Л. Добрецову, А. Г. Кирдяшкину, 1993. Гра­ница химического и фазового переходов на глубине 670 км разделяет нижне- и верхне­мантийное конвективные течения, l₁ — толщина верхней мантии, 1₂ — толщина нижней

мантии.

1 — океанская литосфера; 2 — континентальная литосфера; 3 — субдуцировавшая плита и возможные реститы; 4 — граница литосферы; 5 — течения в астеносфере и нижней ман­тии; 6 — возможные течения в переходной зоне «С»