Возрастание, убывание, точки экстремума функции
Производные и дифференциалы неявно заданных функций
Для функции двух переменных 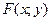 напишем уравнение
напишем уравнение 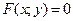 , (3) которое устанавливает соответствие между ее равноправными переменными
, (3) которое устанавливает соответствие между ее равноправными переменными 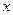 и
и 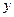 . Такое соответствие порождает неявно заданную функцию
. Такое соответствие порождает неявно заданную функцию 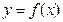 (или
(или 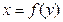 ). В теории функций нескольких переменных мы получим прямые формулы для вычисления производных таким образом заданных функций. Тем не менее наших знаний достаточно, чтобы уже сейчас вычислять производные этих функций. Для этого надо в формуле (3) вычислить обычную производную по переменной
). В теории функций нескольких переменных мы получим прямые формулы для вычисления производных таким образом заданных функций. Тем не менее наших знаний достаточно, чтобы уже сейчас вычислять производные этих функций. Для этого надо в формуле (3) вычислить обычную производную по переменной 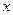 , считая, что это сложная функция, содержащая внутреннюю функцию
, считая, что это сложная функция, содержащая внутреннюю функцию 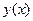 .
.
Пример 1. Для функции 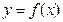 , заданной неявно уравнением
, заданной неявно уравнением 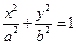 найдите
найдите 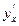 и
и 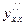 .
.
Решение. От функции 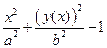 вычислим производную по переменной
вычислим производную по переменной 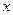 и получим
и получим 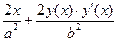 и приравняем ее к 0. Отсюда найдем
и приравняем ее к 0. Отсюда найдем 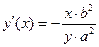 . Вторую производную найдем как производную от первой производной
. Вторую производную найдем как производную от первой производной 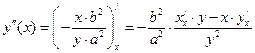 . Подставляя сюда уже найденную первую производную
. Подставляя сюда уже найденную первую производную 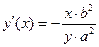 , найдем
, найдем 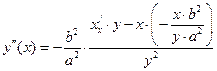 . С учетом того, что
. С учетом того, что 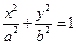 , получим в итоге
, получим в итоге 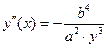 . Нарисуйте эллипс
. Нарисуйте эллипс 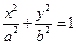 и посмотрите на геометрический смысл полученных результатов.
и посмотрите на геометрический смысл полученных результатов.
Возрастание, убывание, точки экстремума функции
Определение 1. Пусть функция 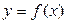 определена на множестве
определена на множестве  и числа
и числа 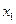 ,
, 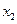 принадлежат множеству
принадлежат множеству 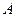 . Если из условия
. Если из условия 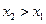 (*) следует, что
(*) следует, что 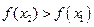 , функция
, функция 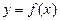 называется возрастающей на множестве
называется возрастающей на множестве  . Если из условия (*) следует, что
. Если из условия (*) следует, что 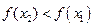 , функция
, функция 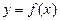 называется убывающей на множестве
называется убывающей на множестве  . Если из условия (*) следует, что
. Если из условия (*) следует, что 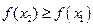 , функция
, функция 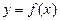 называется неубывающей на множестве
называется неубывающей на множестве 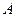 . Если из условия (*) следует, что
. Если из условия (*) следует, что 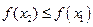 , функция
, функция 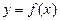 называется невозрастающей на множестве
называется невозрастающей на множестве 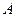 . Во всех этих случаях функция называется монотонной на множестве
. Во всех этих случаях функция называется монотонной на множестве 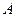 .
.
Определение 2. Точка 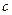 называется точкой максимума функции
называется точкой максимума функции 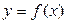 , если существует число
, если существует число 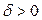 такое, что функция
такое, что функция 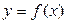 определена на интервале
определена на интервале 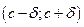 и
и 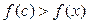 при
при 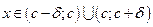 .
.
Определение 3. Точка 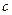 называется точкой минимума функции
называется точкой минимума функции 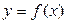 , если существует число
, если существует число 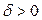 такое, что функция
такое, что функция 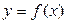 определена на интервале
определена на интервале 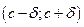 и
и 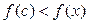 при
при 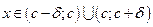 .
.
Определение 4. Точки максимума и минимума функции 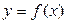 называются точками экстремума функции
называются точками экстремума функции 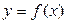 .
.
Теорема 1. Пусть для функции 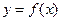 выполнено условие
выполнено условие 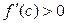 , тогда существует число
, тогда существует число 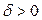 такое, что функция
такое, что функция 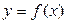 возрастает на интервале
возрастает на интервале 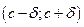 .
.
Доказательство. По условию теоремы 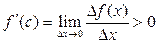 . Следовательно, при достаточно малых
. Следовательно, при достаточно малых 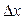 выполнено условие
выполнено условие 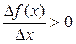 , т. е. большему значению аргумента соответствует большее значение функции. Отсюда функция возрастает и теорема доказана.
, т. е. большему значению аргумента соответствует большее значение функции. Отсюда функция возрастает и теорема доказана.
Теорема 2. Пусть для функции 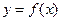 выполнено условие
выполнено условие 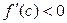 , тогда существует число
, тогда существует число 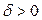 такое, что функция
такое, что функция 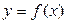 убывает на интервале
убывает на интервале 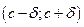 .
.
Доказательство. По условию теоремы 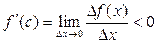 . Следовательно, при достаточно малых
. Следовательно, при достаточно малых 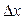 выполнено условие
выполнено условие 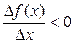 , т. е. большему значению аргумента соответствует меньшее значение функции. Отсюда функция убывает и теорема доказана.
, т. е. большему значению аргумента соответствует меньшее значение функции. Отсюда функция убывает и теорема доказана.
| <== предыдущая лекция | | | следующая лекция ==> |
| Курареподобные средства. | | | Теоремы Ролля, Лагранжа, Коши |
Дата добавления: 2015-11-28; просмотров: 895;
