Расчет пластового давления и дебитов скважин
При определении забойного давления в скважинах с целью выбора способов подъема жидкости из глубины на дневную поверхность, оценки фазового состояния нефти и воды, а также для вычисления градиентов пластового давления с целью определения скоростей перемещения фильтрующихся веществ, границ разделов между нефтью и водой необходимо знать поле пластового давления.
При решении задач фильтрации неоднородных жидкостей, в частности нефти и воды, наряду с вычислением поля водонасыщенности определяют и поле пластового давления. В случае вытеснения нефти водой из прямолинейного или радиального пласта при использовании модели поршневого вытеснения поле давления вычисляется просто по формулам, приведенным в предыдущем разделе.
В случае непоршневого вытеснения нефти водой даже из прямолинейного пласта распределение давления в нем устанавливать несколько сложнее. Поэтому рассмотрим последний случай более подробно.
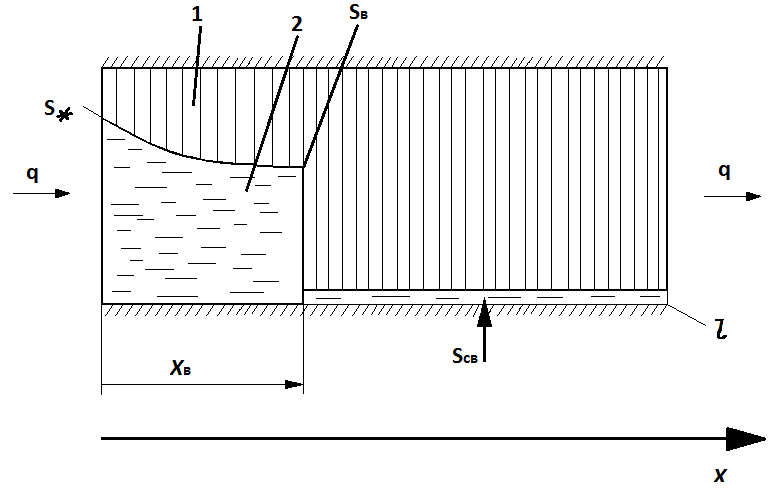
Рис. 7.14 - Схема непоршневого вытеснения нефти водой
из прямолинейного пласта: 1 - нефть; 2 - вода
Согласно рис. 7.14 имеем следующее выражение для суммарной скорости фильтрации нефти и воды в пласте:
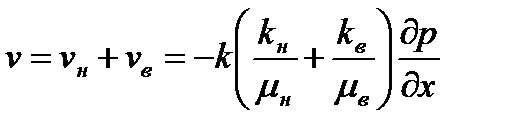 . .
| (7.85) |
Отсюда, учитывая выражение для функции 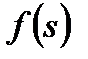 , получим
, получим
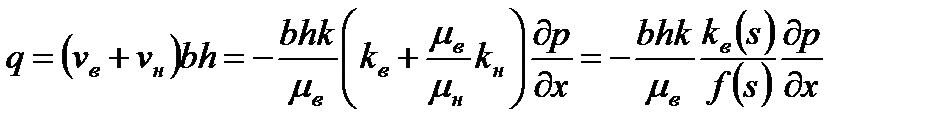 . .
| (7.86) |
При этом для простоты будем полагать в данном параграфе, что объем закачанной в пласт воды 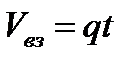 . Поскольку
. Поскольку
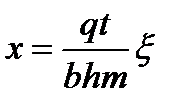 ;
; 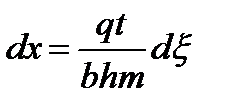 ,
,
после их подстановки в (7.86) имеем
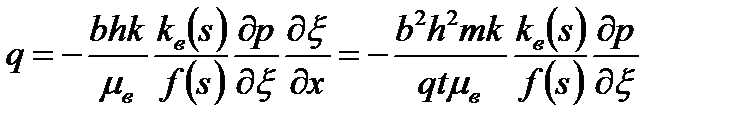 . .
| (7.87) |
Учитывая, что 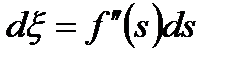 , получим из (7.87), заменяя частные производные обыкновенными,
, получим из (7.87), заменяя частные производные обыкновенными,
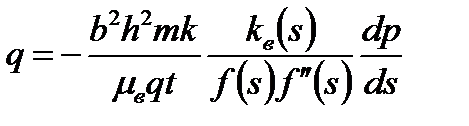 ,
,
или
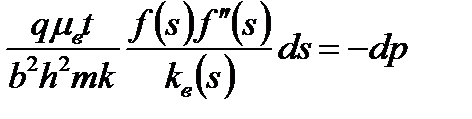
| (7.88) |
Согласно рис. 7.14 в области пласта при 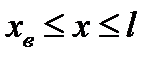 движется чистая нефть. Будем считать, что фазовая проницаемость для нефти в этой области равна абсолютной. Тогда для полного перепада давления
движется чистая нефть. Будем считать, что фазовая проницаемость для нефти в этой области равна абсолютной. Тогда для полного перепада давления 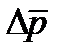 в прямолинейном пласте получим следующее выражение:
в прямолинейном пласте получим следующее выражение:
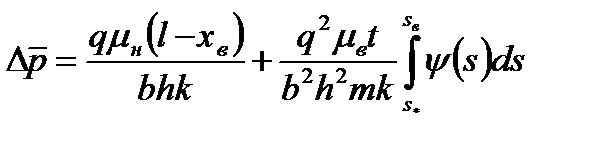 ; ;
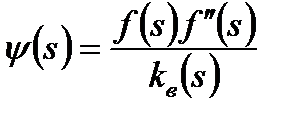 ; ;
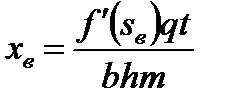 . .
| (7.89) |
Интеграл от функции водонасыщенности 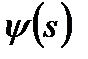 можно вычислить численным путем с использованием ЭВМ. При этом входящую функцию
можно вычислить численным путем с использованием ЭВМ. При этом входящую функцию 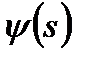 и вторую производную функции
и вторую производную функции 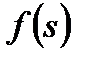 можно найти путем численного дифференцирования.
можно найти путем численного дифференцирования.
В радиальном случае имеем
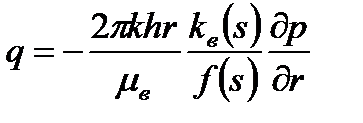 . .
| (7.90) |
Дифференцируя формулу (7.82), имеем
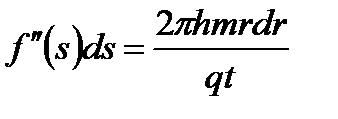 . .
| (7.91) |
Подставляя (7.91) в (7.90) и заменяя частную производную на обыкновенную, получим
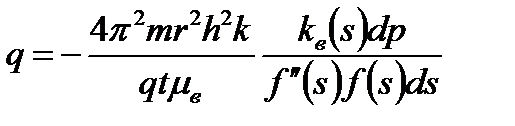
или
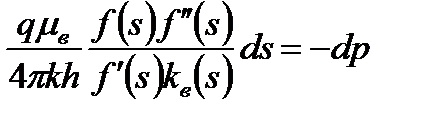 . .
| (7.92) |
Для полного перепада давления 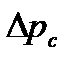 между скважиной и контуром питания получим следующее выражение:
между скважиной и контуром питания получим следующее выражение:
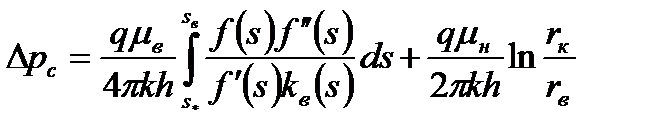 . .
| (7.93) |
При решении плоских задач вытеснения нефти водой численными методами на ЭВМ поле пластового давления вычисляют одновременно с полем водонасыщенности и нефтенасыщенности.
На практике бывает важно определить перепады забойного давления между нагнетательными и добывающими скважинами не во все периоды, а в определенные моменты разработки, например в начальный ее период, когда в пласте движется одна практически не обводненная нефть, или в некоторые моменты после начала обводнения добываемой из пласта продукции.
Практически важно приближенно определить перепады давлений. Поэтому при таких расчетах можно использовать метод эквивалентных фильтрационных сопротивлений.
Рассчитаем распределение пластового давления при трехрядной схеме расположения скважин по методу эквивалентных фильтрационных сопротивлений. Для простоты возьмем однородный пласт и допустим, что происходит поршневое вытеснение из него нефти водой.
Рассмотрим тот случай, когда процесс заводнения только начался и нефть вытеснена лишь из области 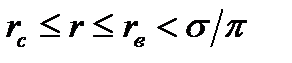 вокруг нагнетательной скважины радиусом
вокруг нагнетательной скважины радиусом 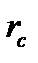 (рис. 7.15).
(рис. 7.15).
D QBCG7yb+h82YeLOLbSOUsjTGj5MeED30uGVHIGVnCbsF9Nc7pge9zceTd57JdrPtxIiDbx0puF1E IJAqZ1qqFXy8P98kIHzQZHTnCBV8oYddfnmR6dS4id5wLEMtOIR8qhU0IfSplL5q0Gq/cD0S7z7d YHXgdqilGfTE4baTyyi6k1a3xBca3eNDg9WxPFkF8dNLWfTT4+t3IWNZFKMLyXGv1PXVfL8FEXAO fzD86rM65Ox0cCcyXnQKlkm0YZSLdQyCgdVqswZxOA9knsn/H+Q/AAAA//8DAFBLAQItABQABgAI AAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsB Ai0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsB Ai0AFAAGAAgAAAAhAKUqFJzoAQAA4AMAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1s UEsBAi0AFAAGAAgAAAAhAMFvjHneAAAACQEAAA8AAAAAAAAAAAAAAAAAQgQAAGRycy9kb3ducmV2 LnhtbFBLBQYAAAAABAAEAPMAAABNBQAAAAA= " strokecolor="black [3040]"/> 
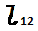
| Z |
| 2σ |
Рис. 7.15 - Схема части полосы трехрядной системы разработки:
1 и 3 - соответственно первый и второй ряд добывающих скважин;
2 - ряд нагнетательных скважин.
Будем считать, что в часть полосы разработки, содержащей три ряда добывающих скважин, заключенных между рядами нагнетательных, закачивается вода с расходом 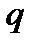 . Длина рассматриваемой части полосы равна
. Длина рассматриваемой части полосы равна 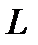 . Таким образом, если взять правый ряд нагнетательных скважин (см. рис. 7.15), то влево от него т.е. в рассматриваемую полосу будет поступать вода с расходом, равным
. Таким образом, если взять правый ряд нагнетательных скважин (см. рис. 7.15), то влево от него т.е. в рассматриваемую полосу будет поступать вода с расходом, равным 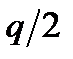 . Остальная часть воды будет уходить в соседнюю полосу, которая должна находиться справа. Так как режим разработки пласта считается водонапорным, объемный расход воды равен объемному дебиту нефти в пластовых условиях. Дебит первого ряда добывающих скважин рассматриваемой части полосы равен
. Остальная часть воды будет уходить в соседнюю полосу, которая должна находиться справа. Так как режим разработки пласта считается водонапорным, объемный расход воды равен объемному дебиту нефти в пластовых условиях. Дебит первого ряда добывающих скважин рассматриваемой части полосы равен 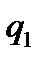 , а дебит второго (центрального) ряда скважин
, а дебит второго (центрального) ряда скважин 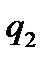 . Поскольку в центральный ряд скважин поступает нефть также слева, то имеем следующее соотношение баланса жидкости в пласте:
. Поскольку в центральный ряд скважин поступает нефть также слева, то имеем следующее соотношение баланса жидкости в пласте:
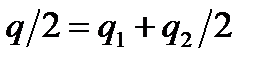 . .
| (7.94) |
Согласно методу эквивалентных фильтрационных сопротивлений, с учетом того, что 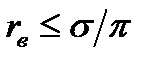 , имеем в соответствии с рис. 7.15.
, имеем в соответствии с рис. 7.15.
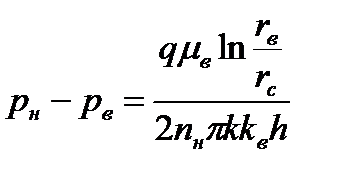 ;
;
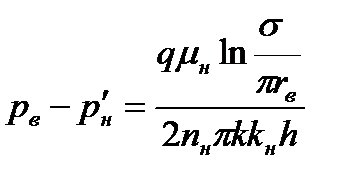 ; ;
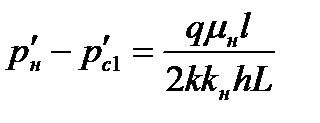 ; ;
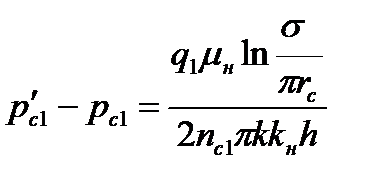 ; ;
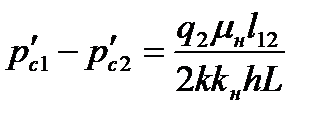 ; ;
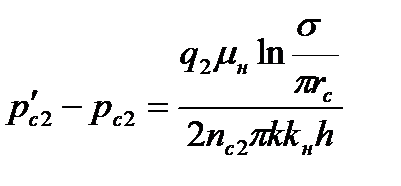 . .
| (7.95) |
Здесь 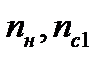 и
и 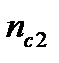 - число скважин соответственно в нагнетательном, первом и втором рядах. Остальные обозначения указаны на рис. 7.15 или соответствуют принятым ранее. Если сложить первые четыре из соотношений (7.95), то получим следующую формулу
- число скважин соответственно в нагнетательном, первом и втором рядах. Остальные обозначения указаны на рис. 7.15 или соответствуют принятым ранее. Если сложить первые четыре из соотношений (7.95), то получим следующую формулу
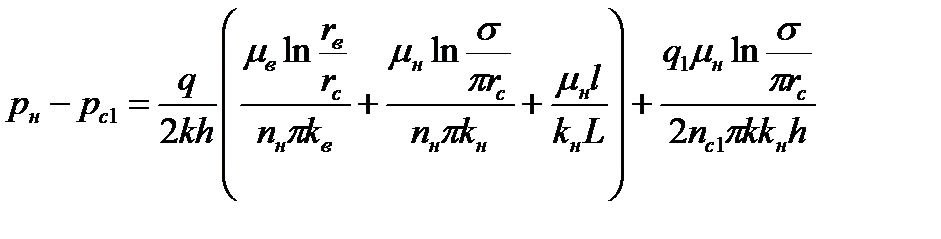 . .
| (7.96) |
Сложим последние три соотношения формул (7.95). В результате получим
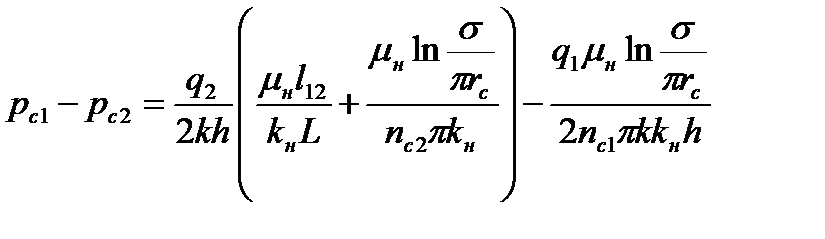 . .
| (7.97) |
Как известно, при расчетах процессов разработки нефтяных месторождений заданы:
1) дебиты скважин, необходимо найти перепады давления между забоями нагнетательных и добывающих скважин;
2) перепады давлений, необходимо найти дебиты рядов скважин.
В первом случае следует использовать формулы (7.96) и (7.97), во втором необходимо решать систему из следующих трех линейных алгебраических уравнений:
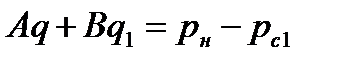 ;
;
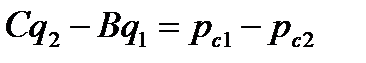 ;
;
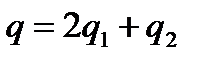 ;
;
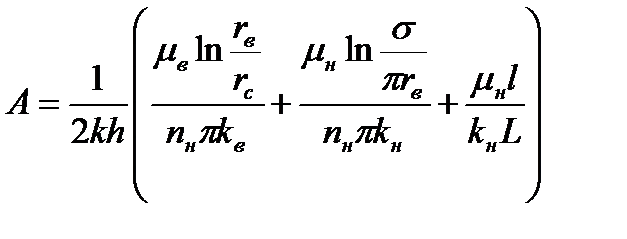 ;
;
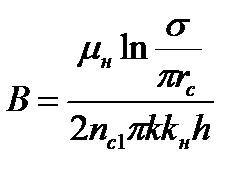 ;
;
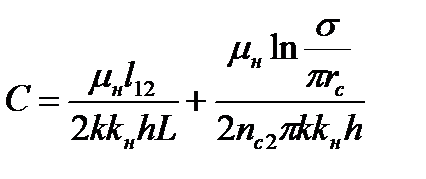 . .
| (7.98) |
Решая эту систему уравнений, получим
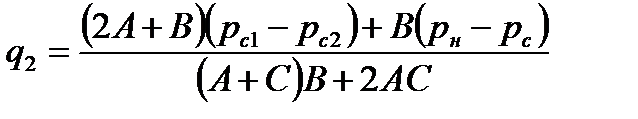 ; ;
| (7.99) |
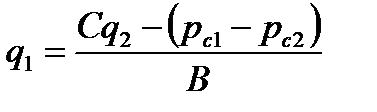 . .
| (7.100) |
Аналогичным образом решают соответствующие задачи в случае пятирядной и других схем расположения скважин.
Дата добавления: 2016-01-03; просмотров: 2256;
