Режимы движения жидкости. Наука о движении жидкостей под действием внешних сил и о механическом взаимодействии жидкости и соприкасающихся с нею тел при их относительном движении
Наука о движении жидкостей под действием внешних сил и о механическом взаимодействии жидкости и соприкасающихся с нею тел при их относительном движении называется гидродинамикой. Рассмотрим некоторые понятия и определения гидродинамики.
Поток жидкости– ряд элементарных струек, движущихся в одном направлении в трубе.
Живое сечение потока– перпендикулярное к основному направлению движения потока его поперечное сечение.
Смоченный периметр– периметр поперечного сечения трубы, с которым соприкасается поток жидкости.
Расход жидкости– количество жидкости, протекающей через живое сечение потока в единицу времени. Определяется по формуле Q = Fv, где F– площадь живого сечения, м2; v– скорость движения жидкости, м/с.
Установившееся течение– основные параметры (скорость и давление) потока жидкости в любой точке потока не изменяются во времени.
Неустановившееся течение– скорость и давление в определенных точках потока жидкости непостоянные, т. е. меняются во времени.
Равномерное течениеосуществляется в потоке, имеющем по длине одинаковые живые сечения, при этом в соответствующих точках сечений скорости и давления одинаковы.
Неравномерное течение– живое сечение по длине потока жидкости меняется или скорости и давления в живых сечениях распределяются неодинаково.
Существуют два режима течения реальной капельной жидкости: ламинарный (струйный) и турбулентный (вихревой). Когда отдельные слои жидкости при малых скоростях движения перемещаются независимо (обособленно) друг от друга, т. е. наблюдается стройное, а именно послойное движение жидкости, – режим называется ламинарный.После достижения определенной скорости движения жидкости слоистое течение ее нарушается и движение становится беспорядочным, бесформенным – турбулентным.
Английским ученым О. Рейнольдсом было доказано, что характер течения зависит от соотношения между скоростью потока, диаметром трубы и вязкостью жидкости. Безразмерный параметр, называемый числом или критерием Рейнольдса, определяется по выражению
Re = vd/v,
где v– средняя скорость потока, м/с;
d– внутренний диаметр трубы, м;
v – коэффициент кинематической вязкости, м2/с
Переход из ламинарного режима в турбулентный (и наоборот) происходит при определенном критическом числе Рейнольдса. При значении Re меньше критического движение потока жидкости ламинарное, при значении больше критического – турбулентное. Ламинарному режиму течения жидкости по гладким металлическим цилиндрическим трубам соответствуют значения Re<C< 2200–2300, турбулентному – Re> 2200–2300. В судовых системах встречаются все виды движения жидкости.
При течении сплошного потока несжимаемой жидкости и установившемся движении в трубе, ограниченной твердыми стенками,расход жидкости в любом живом сечении трубы есть величинапостоянная:
Q = F1v1= F2v2=····=F2v2=const (1.2)
где F1 и F2– площади разных сечений трубы;
v1и v2– средние скорости течения жидкости в данном сечении трубы.
Уравнение (1.2) называется уравнением сплошностиили неразрывности,
К установившемуся сплошному потоку несжимаемой идеальной жидкости, протекающей в жесткой трубе, применим закон сохранения энергии, т. е. энергия любой частицы струйки потока в любом его живом сечении есть величина постоянная и равна Еу= const, где Еу– энергия единицы массы (1 кг) текущей жидкости, или удельная энергия. В общем виде удельная энергия состоит из двух составляющих:
Еу = Еп + Ек,
где Еп– потенциальная энергия; Ек– кинетическая энергия. В свою очередь, Еп = z + р/ρ, где z– удельная энергия положения выделенной единицы массы относительно какой–либо плоскости сравнения, называемая геометрическим напором.
В различных живых сечениях потока геометрический напорможет иметь разные значения. Энергия положения характеризуетработу, которую может произвести масса 1 кг выделенной жидкости при свободном падении с данной высоты. Единица геометрического напора выражается высотой столба жидкости в метрах.Вторая составляющая уравнения (1.3) является удельной энергией давления, т. е. потенциальной энергией 1 кг жидкости,создаваемой гидростатическим давлением, и называется пьезометрическим напором.
p=ρ·h
где ρ – плотность жидкости;
h – высота свободной поверхности жидкости от центра данного сечения
h=р1/ρ, h2 =р2/ρ , …….hn =рn/ρ
Кинетическая энергия жидкости Ек = 0,5 mρ. Отнесенная к 1 кг массы жидкости, т.е. когда m =1/g, кинетическая энергия (скоростной напор) равна Ек=v2/(2g).
Величина Ек может измеряться высотой столба жидкости. Это следует из определения скорости свободно падающего тела v=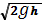 
c,откуда hc=v2/(2g). Поэтому hc– это высота , падая с которой в среде, не имеющей сопротивления, 1 кг жидкости преобретая скорость v. В рассматриваемых живых сечениях потока скоростные напоры будут соответственно равны
v12/(2g).=v22/(2g).,….,v2п/(2g)..
Еу = z1 + р1/ρ+v12/(2g).=z2 + р2/ρ+v22/(2g)=….
т.е. z + р/ρ+v2/(2g)= const
Это уравнение называется уравнение Бернулли. Согласно этому уравнению полная удельная энергия идеальной жидкости в любом живом сечении элементарной струи будет постоянна.
Уравнение Бернулли можно истолковать и чисто геометрически. В самом деле, каждый член этого уравнения имеет линейную размерность.
При движении реальной (вязкой) жидкости скорости в сечении потока будут различны, что изменит значение энергии жидкости, проходящей в единицу времени через сечение потока. Неравномерность скоростей по сечению потока учитывается коэффициентом Кориолиса а, который равен 1,05–1,1 и в расчетах часто опускается.
Помимо учета неравномерности распределения скоростей по сечению потока для реальной жидкости необходимо учитывать потери напора на преодоление сопротивлений.
Потеря напора hwпри движении жидкости по трубопроводам, в свою очередь, состоит из потери напора по длине трубопровода hTи потери местных сопротивлений йм, т. е. hw= hT+ hM.
Дата добавления: 2016-01-03; просмотров: 1092;