Контактная разность потенциалов
Рассмотрим явления в контакте металл – полупроводник при отсутствии поверхностных состояний. Возьмем контакт электронного полупроводника (n-типа) и металла в предположении, что работа выхода электрона из полупроводника ФП меньше работы выхода электрона из металла ФМ, то есть ФП < ФП. На рисунке 1а показана зонная энергетическая диаграмма металла (Me) и полупроводника (П/П) не находящихся в контакте друг с другом. Термодинамическая работа выхода – это расстояние от уровня вакуума Е0 до уровня Ферми в металле FМ или в полупроводнике FП:
| ФМ = F0 – FМ | (1а) | |
| ФП = F0 – FП | (1б) |
Если металл и полупроводник привести в непосредственный контакт (рис.1б), то электроны будут переходить преимущественно из полупроводника в металл, так как уровень Ферми в полупроводнике в момент соединения с металлом лежит выше, чем в металле, т.е.
FП > FМ. При этом металл заряжается отрицательно, а полупроводник – положительно.
Направленный поток электронов проходит над потенциальным барьером, который возникает в при контактной области полупроводника (рис. 1в). Указанный поток электронов будет иметь место до тех пор, пока уровни Ферми FП и FМ не выровняются, после чего установится динамическое равновесие (токи jП и jМ будут равны друг другу). Между металлом и полупроводником возникает контактная разность потенциалов
| Uk = (FП - FМ) / e | (2) |
где е – абсолютная величина заряда электрона.
При выводе выражения (2) разность уровней FП - FМ берется из рис. 1а (или рис. 1б), так как после установления равновесия (рис. 1в) FП = FМ. Величина ϕМ – это высота потенциального барьера со стороны металла, она имеет смысл работы выхода электронов из металла в полупроводник, равной расстоянию от уровня Ферми до зоны проводимости на границе. В глубине проводника величина F = EC – FП, согласно рис. 1в. При этом имеет место следующее равенство:
| ϕМ = e * Uk + F | (3) |
Таким образом, в при контактной области полупроводника возникает слой положительного объемного заряда толщиной L, рис. 1в. Из этого слоя все электроны перемещены в металл. В физике полупроводников доказывается, что толщина этого слоя
| L = √(2 ε ε0 Uk / e n0) | (4) |
где ε – диэлектрическая проницаемость полупроводника, ε0 – электрическая постоянная, n0 –концентрация свободных электронов в глубине полупроводника (т.е. при x > L).

Рис. 1. Зонная энергетическая диаграмма контактной системы «металл – полупроводник» в отсутствии внешнего электрического поля
Величина L обычно составляет 10÷100 нм. Концентрация свободных электронов в металле значительно больше, чем в полупроводнике, поэтому толщина отрицательного слоя объёмного заряда в металле ничтожно мала, и она не дает вклада в контактную разность потенциалов. Толщина слоя объёмного заряда L называется длиной экранирования Дебая. Этот слой экранирует внутреннюю часть полупроводника от проникновения туда контактного поля.
Рассмотрим условие динамического равновесия при контакте металла и полупроводника (см. рис. 1в). Ток термоэлектронной эмиссии электронов из металла в полупроводник над потенциальным барьером высотой ϕM дается уравнением Ричардсона-Дэшмена:
| JM = S * A * T2 * exp (ϕM / kT), | (5) |
где А – постоянная, Т – абсолютная температура, k – постоянная Больцмана, S – площадь контакта.
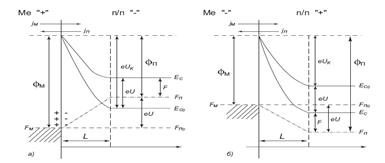
Рис. 2. Зонная диаграмма контактной системы «металл – полупроводник»
а) при положительном напряжении; б) при отрицательном напряжении
Обратный ток термоэлектронной эмиссии электронов из полупроводника в металл jП равен
| JП = S * A * T2 * exp ((eUК + F) / kT), | (6) |
где величина eUК + F играет роль работы выхода электрона из полупроводника в металл. При динамическом равновесии jМ = jП. Этот же вывод следует и из уравнения (3).
2. Вольт-амперная характеристика контактной системы «металл – полупроводник»
Наличие потенциального барьера на границе металл – полупроводник приводит к тому, что возможно явление выпрямления переменного тока, а ВАХ для постоянного тока будет несимметричной. За положительное напряжение U примем такое напряжение, когда металл имеет положительный потенциал относительно полупроводника. Так как в области объемного заряда L свободных электронов практически нет, то удельное сопротивление этой области очень велико и все внешнее напряжение будет падать в этой области. При U > 0 все уровни в полупроводнике сдвинутся вверх на величину eU (см. рис. 2а). Переход электронов из полупроводника в металл облегчится, высота барьера со стороны полупроводника уменьшится, а со стороны металла высота барьера останется той же самой - ϕМ. Результирующий поток электронов направлен от полупроводника к металлу и увеличивается с ростом внешнего напряжения. При U < 0 все энергетические уровни в полупроводнике сдвинутся вверх на величину eU (см. рис.2б) и высота потенциального барьера со стороны полупроводника увеличится, а со стороны металла вновь не изменится. Вследствие этого поток электронов jП со стороны полупроводника уменьшится, и при увеличении U этот поток станет очень мал. Поэтому через барьер будет проходить только постоянный поток электронов из металла. В общем случае при любой полярности напряжения результирующий ток j = jП – jМ. Из диаграммы, представленной на рис. 2, при любой полярности приложенного напряжения получим:
· ток, обусловленный термодинамической эмиссией электронов из металла в полупроводник
по-прежнему дается формулой (5).
· ток, обусловленный термодинамической эмиссией электронов из полупроводника в металл:
| jП = S * A * T2 * exp (-ϕП / kT) | (7а) | |
| jП = S * A * T2 * exp ( (eUК - ϕМ) / kT) | (7б) |
· уравнение (3) остается справедливым и при наличии внешнего напряжения. Результирующий ток равен:
| J = jМ * (exp ( eUК / kT) - 1), | (8) |
где jМ дается формулой (5).
Используя уравнение (3), можно записать для тока:
| jМ = S * A * T2 * exp (-ϕМ / kT) | (9а) | |
| jМ = S * A * T2 * exp ( - (eUК + F) / kT) | (9б) |
Вольт-амперная характеристика (ВАХ), построенная по уравнению (8), показана на рис. 3 (кривая 1). При eU >> kT ток быстро (экспоненциально) растет. При eU >> kT (но U < 0) ток становится постоянным jS ≡ jМ, то есть не зависящим от U, и малым. Этот ток jS получил название тока насыщения.
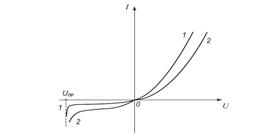
Рис. 3. Вольт-амперная характеристика выпрямляющего контакта полупроводника с металлом
1 – диодная теория; 2 – диффузионная теория
Приведенный вывод ВАХ получил название диодной теории. Эта теория справедлива, если токи jМ и jП обусловлены термоэлектронной эмиссией, когда электроны вылетают из металла или полупроводника с тепловыми скоростями υT. В рассматриваемом случае эти электроны вылетают не в вакуум, а должны пролететь через слой объёмного заряда толщиной L без столкновений с атомами решетки полупроводника. Если же длина свободного пробега электрона l значительно меньше толщины барьера L (l << L), то электрон в процессе перехода испытывает много столкновений с решеткой и быстро теряет свою тепловую скорость направленного движения. Электрон будет двигаться через барьер под действием электрического поля напряжённостью E с дрейфовой скоростью
| υ = μ * Е , | (10) |
где μ – подвижность электронов.
Величина токов будет определяться формулой:
| J = S ⋅ e ⋅μ ⋅ n(x) ⋅ E(x), | (11) |
где поле E(x) и концентрация n(x) электронов может зависеть от координаты x.
Так будет в области барьера, где объемный заряд, обусловленный контактной разностью потенциалов, делает поле E(x) неоднородным. Ток, протекающий через полупроводник, должен быть одинаков в любом поперечном сечении полупроводника. Согласно статистике электронов в энергетических зонах полупроводника известно, что концентрация электронов в зоне проводимости равна:
| n = NС * exp ( - (ЕС - ЕП) / kT), | (12а) | |
| n = NС * exp ( - F / kT), | (12б) |
где NC – эффективная плотность состояний в зоне проводимости полупроводника.
При отсутствии внешнего напряжения, вблизи границы F = EС − EП = ϕМ Поэтому концентрация свободных электронов в полупроводнике у самой границы (при x = 0):
| n s = NС * exp ( - ϕМ / kT). | (13) |
Как видно из рис. 2а и 2б, величина ns не изменяется при приложении внешнего напряжения любой полярности, так как около границы величина F = EC – EП = ϕМ от напряжения U не зависит. Напряженность электрического поля Es в полупроводнике около границы с металлом (при x = 0) равна
| E s = (U + Uк) / L. | (14) |
так как в этом случае поля, создаваемые внешним напряжением U и контактной разностью потенциалов UК складываются.
При U = 0 в состоянии динамического равновесия результирующий ток j = jП - jМ = 0 . Из уравнений (11), (13) и (14) при U = 0 получим:
| Js = S * e *μ * ns * Es, | (15а) | |
| Js = S * e *μ * Ns * (Ux / L) * exp (-ϕМ / kT). | (15б) |
Эти уравнения определяют ток, создаваемый потоком электронов из полупроводника в металл под действием контактного поля EК = Uк / L . Но при равновесии jП = jМ . Последнее значит, что из металла в полупроводник течёт такой же электронный ток jМ , но он имеет диффузионную природу, так как в слое объёмного заряда n = n(x) – концентрация свободных электронов зависит от координаты. При подаче напряжения U из тех же уравнений (11), (13) и (14) получим, что диффузионный поток электронов из металла через барьерный слой в полупроводнике создает ток
| Js = S * e *μ * Ns * ((Uк + U) / L) * exp (-ϕМ / kT). | (16) |
Видно, что напряжение U увеличивает диффузионный ток (сравните уравнения (14) и (15)). Связано это с тем, что напряжение U изменяет вид распределения n(x). Однако обратный поток электронов из полупроводника в металл j изменяется из-за изменения высоты потенциального барьера со стороны полупроводника под влиянием напряжения U.
| JП = JМ * exp (e U / kT). | (17) |
В итоге результирующий ток j = j П − j М будет равен:
| J = JS * (exp (e U / kT) - 1), | (18) |
что по форме совпадает с уравнением (8), но только ток насыщения jS определяется не уравнением (9), а уравнением (16). Используя (3), получим:
| Js = S * e *μ * Ns * ((Uк + U) / L) * exp (- (eU + F) / kT). | (19) |
Рассмотренная теория получила название диффузионной теории. ВАХ, даваемая уравнением (16), показана на рис. 3 (кривая 2). Ток «насыщения» jS из (14) теперь зависит от приложенного напряжения, что часто наблюдается экспериментально.
В литературных источниках уравнение (19) принято представлять в виде:
| Js = S * e *μ * n0 * ((Uк + U) / L) * exp (- eUк / kT), где n0 = Ns * exp (- F / kT) (n0 – концентрация свободных электронов в глубине полупроводника (при x > L)). | (20) |
В заключение отметим, что слой объёмного заряда L получил название запирающего слоя, а потенциальный барьер – барьера Шоттки. Напряжение U > 0 называется прямым, а U < 0 – обратным. Поэтому соответственно говорят о прямых и обратных токах через контакт.
Одностороннюю проводимость контактов металл – полупроводник используют для изготовления полупроводниковых усилителей переменного тока. Для выпрямления технических токов низкой частоты (f = 50 Гц) широко применяют селеновые выпрямители, в которых запирающий слой образуется у границы слоя Se и металлического электрода. Металлический электрод обычно состоит из сплава различных металлов (например, Bi, Cd и Sn). Для выпрямления токов высокой частоты применяют германиевые и кремниевые «точечные» СВЧ-детекторы. К пластине полупроводника прижимается или приваривается металлическая проволока малого диаметра (микроны).
Контактные системы типа «металл – полупроводник» широко используют для создания быстродействующих нелинейных элементов, которые часто называются диодами Шоттки. В уравнениях (8) диодной теории и (17) диффузионной теории величины токов jП и js определяются при U → 0 . Воспользуемся уравнением вольт-амперной характеристики диффузионной теории и определим дифференциальное сопротивление p-n перехода при очень малых значениях напряжения.
| ln R = (eUк / kT) + lnA, где А = ln j0 + ln(Uк / L) + ln(kT / e). | (21) |
Графическая зависимость ln R – 1/T позволяет определить величину контактной разности потенциалов Uк:
| (Δ ln R) / (Δ 1 / T) = eUк / k. | (22) |
Тангенс угла наклона экспериментальной зависимости ln R – 1/T , домноженный на параметр ke, дает значение Uк.
| Uк = ((k /e) * (Δ ln R)) / (Δ 1 / T) | (23) |
Если все величины имеют размерность системы СИ, то величина контактной разности потенциалов Uк выражена в вольтах.
| <== предыдущая лекция | | | следующая лекция ==> |
| Процесс создания микроструктур в рамках представлений алгоритмической энтропии | | | Общие принципы работы сканирующих зондовых микроскопов |
Дата добавления: 2016-01-03; просмотров: 2014;
