Процесс создания микроструктур в рамках представлений алгоритмической энтропии

Как упоминалось выше, упорядоченные атомные микроструктуры можно рассматривать как своеобразную матрицу памяти, в которой «записано» функциональное назначение изделия. С этой точки зрения можно считать, что в атомной структуре проведено кодирование определенной дискретной информации, посредством упорядоченного (с точки зрения реализации необходимого функционального назначения) размещения атомов. Подобный подход позволяет при проведении анализа энтропийных параметров микроструктур использование теории кодирования дискретной информации. Возможность использования теории кодирования дискретной информации основана на том факте, что реальные микро- и наноструктуры могут быть представлены в виде совокупности отдельных атомно-молекулярных слоев (текстов), при этом позиция каждого атома в мономолекулярном слое может рассматриваться в качестве элемент сообщения (слова или буквы).

На рисунке 3.2 представлено схематическое отображение возможного способа информационного «кодирования» твердотельной структуры, на примере упорядоченного расположения индивидуальных атомов в мономолекулярном слое.

При выполнении кодирования предполагается заданной последовательность (как правило, большая) сообщений (объектов) 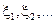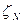вместе со своими вероятностями появления, т.е. как последовательность случайных величин. Следовательно, может быть вычислена соответствующая ей энтропия (и количество информации H, содержащееся в этой случайной последовательности, воспринимаемой как «сообщение»).

Эта информация может быть записана различными способами записи (см. рис.3., в том числе, как это проведено для рассматриваемого случая – спецификой размещения индивидуальных атомов в пределах подложки (изделия).

Представленное выше определение количества информации целесообразно при рассмотрении процессов преобразования информации из одного вида в другой, т.е. при проведении процедуры кодирования информации (технологический процесс, в этой расширенной трактовке, также можно рассматривать в качестве своеобразного кодирования структуры изделия на атомном уровне физической реализации).

Существенно, что при таком преобразовании выполняется закон сохранения количества информации. Здесь можно провести аналогию с законом сохранения энергии. (Этот закон является ключевым основанием для введения понятия энергии). Однако, закон сохранения информации сложнее закона сохранения энергии в двух отношениях. Закон сохранения энергии устанавливает точное равенство энергий при их взаимопревращениях, в процессе эволюции физической системы. При превращении же информации имеет место более сложное соотношение, а именно «не больше - ( 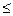)», т.е. информация не может возрастать при проведении кодирования.

Рис. 4. Схематическое отображение фрагмента структуры изделия

в рамках представлений теории кодирования сигналов

Знак равенства соответствует случаю оптимального кодирования. Поэтому, при формулировке закона сохранения информации приходится говорить лишь о возможности существования такого кодирования. Таким образом, должно иметь место равенства количества информационного обеспечения технологии (применительно к рассматриваемому случаю, речь может идти об адекватном соответствии информационного потенциала технологии, в части совершенства оборудования и используемых материалов), и информационного потенциала изделия, изначально заложенного конструктором на этапе проектирования.

Второе обстоятельство состоит в том, что равенство является приближенным (а не точным), асимптотическим, т.е. справедливым для достаточно сложных сообщений (объектов). Точный знак равенства возможен в предельном случае. В последнем случае имеется полная аналогия с законами статистической термодинамики, которые справедливы для систем, состоящих из очень большого числа атомов. Информация может быть записана различными реализациями, в особенности, если речь идет о невырожденной (см. выше) конструкции изделия. Если N – число таких реализаций, то указанный закон сохранения количества информации заключается в равенстве H= lnM, осложняемый упомянутыми двумя обстоятельствами (в действительности H< lnM).

Методология анализа качества технологических процессов, основанная на принципах кодирования случайных последовательностей, может быть распространена на все типы производственных процессов, но ее применение представляется более предпочтительным для случая технологий атомной сборки. Примем, что дискретный процесс создания изделия по технологии атомной сборки является стационарным, т.е. все законы распределения P{ 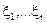} (произвольной кратности r) не меняются при сдвиге:

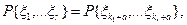
		(25)
где a – любое натуральное число.

Величина сдвига a предполагается такой, что значения {k₁+a,…, k_r+a}не выходят за пределы области K определения параметра k. Предполагается, что эта область определения параметра не ограничена в обе стороны.

В практическом плане, понятие стационарности, оговоренных выше, случайных последовательностей ассоциирует с представлениями об устойчивости (стабильности) реальных технологических процессов в производственной практике создания изделий, и перекликается с, введенными ранее, представлениями об энтропийной устойчивости случайных процессов. Выполнение этого условия позволяет рассмотреть процесс создания изделия на основе методологии теории информации, в части анализа процессов «передачи сообщений» при наличии помех и пропускной способности каналов связи. В последнем случае, под пропускной способностью следует понимать взаимосвязь элементов из всей совокупности информационного обеспечения технологических процессов производства изделия.