ПЕРЕХОДНЫХ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ ЦЕПЯХ

ОСНОВНЫЕ ПОЛОЖЕНИЯ ПО АНАЛИЗУ

Переходные процессы в нелинейных цепях существенно отличаются от переходных процессов в линейных цепях. Нелинейность характеристики какого-либо элемента цепи может привести как к чисто количественному изменению переходного процесса, так и к качественно новым явлениям.

В первом случае нелинейность цепи может увеличить скорость переходного процесса на одном промежутке времени, уменьшить скорость в другом промежутке; при этом может возрасти максимальное значение тока в переходном режиме, однако качественная сторона явления остается без существенных изменений.

Во втором случае за счет нелинейности возникают новые явления, принципиально невозможные в линейной цепи:

а) в линейной цепи включение источника постоянной или гармонической э.д.с. (тока) сопровождается некоторым затухающим переходным процессом, преходящим в принужденный режим, частота которого равна частоте источника; в нелинейной цепи переходный процесс может привести к возникновению колебаний с частотой, отличной от частоты сигнала источника (автоколебаний);

б) в линейной цепи напряжения и токи в переходном процессе обычно можно представить в виде суммы двух составляющих: свободной и принужденной; в нелинейной цепи принцип наложения неприменим и нельзя раскладывать величины на свободные и принужденные составляющие.

Анализ переходного процесса в линейной цепи обычно сводиться к решению системы линейных дифференциальных или алгебраических уравнений. Математический аппарат решения подобных уравнений разработан достаточно полно и задача анализа обычно сводиться к нахождению наиболее экономичного и наглядного метода инженерного расчета. При и этом широко применяются принципы наложения и взаимности. Значительно сложнее обстоит дело с расчетом и анализом переходного процесса в нелинейной цепи. Переходные процессы в нелинейной цепи описываются нелинейными диф. уравнениями, теория которых разработана значительно хуже, чем линейных. Не существует общего метода (подхода) к решению нелинейных уравнений. Существующие в настоящее время методы применимы к решению уравнений определенного типа и не обладают достаточной общностью. Многие нелинейные уравнения в настоящее время вообще не имеют аналитических решений, либо требуют применения специальных функций, неприменимых в инженерной практике. Особенно осложняется дело в том случае, если нелинейность цепи задана графически и отсутствует достаточно простое математическое описание этой нелинейности.

В инженерной практике зачастую достаточно получить хотя бы ориентировочные расчетные соотношения, дающие приближенную количественную оценку процессов в нелинейной цепи. Поэтому в теории нелинейных цепей в настоящее время широко развиты методы приближенных решений.

Существующие в настоящее время методы анализа и расчета переходных процессов в нелинейных цепях можно классифицировать следующим образом:

-по виду операций, которые необходимо выполнить для решения (интегрирования) нелинейных диф. уравнений: а) аналитические; б) графи-ческие; в) графо-аналитические; г) численные;

-по характеру величины, для которой производиться расчет: а) расчет для мгновенных значений токов I и напряжений U; б)расчет для мгновенных значений огибающих токов и напряжений; в)расчет для медленно меняющихся составляющих.

Под аналитическими методами расчета понимают такие, в которых основной операцией при определении зависимостей искомых токов и напряжений от времени является точное или приближенное аналитическое интегрирование диф. уравнений цепи, в которых учтены аналитические выражения характеристик нелинейных элементов. Следует иметь в виду, что только сравнительно простые уравнения (невысокого порядка) допускают аналитическое решение. Достоинство аналитических методов состоит в том, что они дают возможность получить решение в общем виде, а не для какого-то конкретного сочетания параметров цепи. Анализ решения в общем виде позволяет выяснить все особенности переходного процесса при изменении параметров элементов цепи.

При использовании графических (графо-аналитических) методов расчета основными операциями при определении зависимости i(t) и u(t) являются графические построения, сопровождающиеся некоторыми численными расчетами. Преимущества графических методов перед аналитическими:

-не требуется представлять характеристики нелинейных элементов в аналитическом виде, что освобождает решение от погрешности аппроксимации;

-довольно просто позволяют учесть наличие гистерезиса или других сложных нелинейных зависимостей.

Графические и графо-аналитические методы применимы к решению нелинейных диф. уравнений невысокого порядка (в основном 1-го и 2-го).

Разработано много способов численного решения диф. уравнений. При их применении решение вычисляется шаг за шагом, а результат представляет собой таблицу соответствующих значений независимой и зависимых переменных. Иногда в процессе численного решения применяют промежуточные графические построения, что не меняет существа метода. Любое уравнение может быть решено численными методами. Для этого должны быть численно заданы конкретные значения всех параметров и начальные условия. Получаемое решение соответствует именно этому конкретному случаю.

Общность численных методов велика, т.к. ими можно воспользоваться для решения любого диф. уравнения. Однако численное решение сложного уравнения требует выполнения большого объема вычислительных работ, что предопределяет применение ЭВМ.

Расчет по огибающим дает возможность, не вдаваясь в мелкие детали процесса внутри каждого периода действующей в схеме периодической э.д.с.(или внутри каждого периода автоколебаний в автоколебательной схеме) судить о макроструктуре процесса. Он применим не только для нелинейных, но и линейных цепей. Конечно, точность расчета по огибающим уступает точности расчета по мгновенным значениям. Однако относительная быстрота расчета по огибающим и возможность судить о макроструктуре переходного процесса часто оказываются решающими факторами. Иногда, где это необходимо, расчет по огибающим дополняют расчетом по мгновенным значениям.

В практических задачах обычно применяют сочетание нескольких методов расчета. Следует иметь в виду, что зачастую нелинейные зависимости бывают заданы (определены) приближенно и могут существенно изменяться с течением времени или при воздействии каких-либо факторов. Поэтому простота и наглядность решения часто бывают более предпочтительны, чем точность математического описания и полнота исходных уравнений.

7.2 АНАЛИТИЧЕСКИЕ МЕТОДЫ

Как уже отмечалось, решение диф.уравнения при анализе переходного процесса в аналитическом виде, если оно только возможно, дает обычно большие преимущества – решение может быть исследовано во всей области его существования. Некоторые из методов, разработанные для решения линейных диф. уравнений, могут быть успешно распространены и на решение нелинейных. Очень часто решение линейного диф. уравнения принимается в виде ряда по степеням независимой переменной. Например, предполагается, что решением уравнения

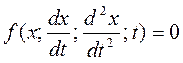
является ряд

.

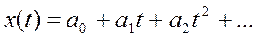Этот ряд подставляют в исходное уравнение и определяют коэффициенты а₀,а_1, а₂,….

Метод определения решения в виде ряда по степеням независимой переменной в некоторых случаях может быть успешно распространен и на нелинейные диф.уравнения. Обычно при этом не удается установить соответствие полученного ряда какой-либо хорошо известной и табулированной функции. Ряд дает лишь формальное решение уравнения в том смысле, что он удовлетворяет уравнению, будучи в него подставленным.

Большинство аналитических методов решения нелинейных уравнений, реализующих указанный подход, хоть и не совпадают в подробностях, но в основном соответствуют этапам, представленным на следующей схеме (рис. 7.1):

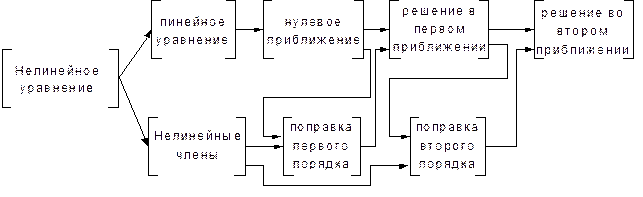
Рисунок 7.1

Суть схемы в следующем:

1) исходное нелинейное уравнение разбивают на две части; одну из них составляет линейное уравнение, достаточно простое, чтобы получить его точное решение; другая содержит все слагаемые, которые приводят к затруднениям, и обычно включают в себя нелинейные члены; в результате решения линейного уравнения получают некоторую функцию, называемую нулевым приближением (или порождающим решением).

2) нулевое приближение каким-либо способом используется с нелинейными членами исходного уравнения для того, чтобы получить поправочные члены (поправку) первого порядка;

3) полученные поправочные члены 1-го порядка объединяются с нулевым приближением для получения решения исходного уравнения в первом приближении; вид объединения поправочных членов и нулевого приближения определяется характерными особенностями применяемого метода; если влияние нелинейности мало, однократное применение описанной процедуры приводит к первому приближению решения, которое может дать точные результаты;

4) при значительной нелинейности иногда можно достичь большей точности, применив тот же метод вторично, что приводит ко второму приближению решения. Дальнейшие повторные применения теоретически возможны, но на практике не применяются из-за существенного роста трудности вычислений.