ИНТЕГРИИУЕМОЙ НЕЛИНЕЙНОЙ АПРОКСИМАЦИИ

Расчет переходного процесса можно осуществить путем аппроксимации характеристик нелинейных элементов цепи такими функциями, которые:

а) достаточно точно отображают характеристики нелинейных элементов на предполагаемом интервале перемещения его рабочей точки,

б) дают возможность проинтегрировать диф. уравнения в известных функциях.

Метод применим в основном к цепям постоянного тока, сводящимся к диф. уравнениям 1-го порядка. При определенных допущениях он может быть применим и к расчету цепей переменного тока тоже 1-го порядка.

7.4 МЕТОД КУСОЧНО-ЛИНЕЙНОЙ АППОКСИМАЦИИ

Аппроксимация характеристики нелинейного элемента цепи отрезками прямых линий дает возможность перейти от нелинейного диф.уравнения к нескольким линейным уравнениям, отличающимся лишь коэффициентами.

Каждое из линейных уравнений справедливо для того интервала времени, в течении которого рабочая точка перемещается по данному линеаризованному участку. Решения, полученные для каждого из линейных участков, припасовывются одно к другому соответствующим выбором постоянных интегрирования. Основная трудность расчета данным методом заключается в определении постоянных интегрирования и времени работы на каждом из линейных участков. Для решения сложных уравнений рационально привлечение ЭВМ.

7.5 ГРАФИЧЕСКИЕ МЕТОДЫ

В тех случаях, когда не требуется высокая точность, для решения диф. уравнения невысокого порядка можно воспользоваться графическим построением. Большинство графических методов анализа переходных процессов в принципе подобно численным. Различие заключается в том, что для сокращения вычислений используется некоторое графическое построение. Точность зависит от способа построения и растет с увеличением масштаба графика. Обычно графический метод прост в применении и может оказаться весьма полезным в качестве первой попытки исследования переходного процесса в нелинейной цепи. В то же время графический метод может в короткое время дать значительную качественную информацию о переходном процессе, после чего дополнительные более точные сведения можно получить другими методами.

7.6 ИЗОБРАЖЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ

НА ФАЗОВОЙ ПЛОСКОСТИ

Переходные процессы можно рассматривать в различных системах координат, например: (i, t), (u, t), (q, t) и др. Качественное исследование различных процессов в цепях, описываемых диф. уравнениями 1-го и 2-го порядков, часто производится с помощью фазовой плоскости.

Фазовой плоскостью называется плоскость, по оси абсцисс которой откладывается исследуемая величина x(t), а по оси ординат – производная от исследуемой величины 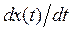( пусть y(t) ).

В каждой конкретной задаче под x понимают i, u, q или др. Любому сочетанию значений x и y исследуемой цепи соответствует вполне определенная точка фазовой плоскости. Переходный процесс в указанной системе координат, как совокупность точек с координатами 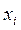и и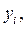зображается кривой, которая для реальной физической цепи ограничена в направлении обеих осей координат, т. к. исследуемая величина x и ее производная 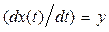конечны в любой момент времени.

Указанный способ изображения переходных процессов (и установившихся процессов) на фазовой плоскости иногда значительно облегчает интегрирование нелинейных диф. уравнений, сводя их решение к геометрическому построению. Изображение на фазовой плоскости дает качественное представление о характере переходного процесса без решения диф. уравнения в конечном виде.

Как правило качественное исследование представляет собой выявление общих свойств исследуемой цепи. Под общими свойствами обычно понимают:

а) выяснение зависимости характера переходного процесса от н.у.;

б) выясне-ние возможности возникновения в цепи автоколебаний, резонансных явлений, автомодуляции;

в) исследование устойчивости перечисленных режимов и состояния (режима) равновесия.

Для качественного исследования переходного процесса в цепях, описываемых уравнениями 3-го порядка, применяют трехмерное фазовое пространство. По осям декартовой системы этого пространства откладывают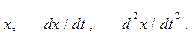

Каждому состоянию исследуемой цепи соответствует определенное сочетание значений x и 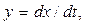т. е. вполне определенная точка на фазовой плоскости. Эта точка носит название изображающей (или представляющей).Всякое изменение состояния цепи изображается на фазовой плоскости в виде некоторой кривой 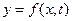, называемой интегральной. Зависимости 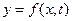, получаемые из решения диф. уравнения цепи, определяют на фазовой плоскости целое семейство интегральных кривых. Каждая из этих кривых соответствует определенному значению постоянной интегрирования, определяемой из начальных условий (н.у.) Совокупность кривых 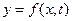, соответствующих различным н.у. , называют фазовым портретом цепи.

Начальное положение изображающей точки на фазовой плоскости определяется значениями x (t=0) и y (t=0), т. е. н.у. Интегральная кривая, проходящая через точку фазовой плоскости с заданными н.у., называется фазовой траекторией. Вид фазовой траектории зависит от конфигурации схемы, от характера нелинейности, от соотношения между параметрами цепи.

В верхней полуплоскости фазовой плоскости, где 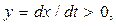изображающая точка может перемещаться только направо в направлении возрастающих значений . Для нижней полуплоскости 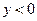и изображающая точка может перемещаться только влево. Таким образом, движение изображающей точки может происходить только по направлению часовой стрелки.

Если переходный процесс описывается диф. уравнением 1-го порядка, то все фазовые траектории лежат на одной кривой и изображающая точка может перемещаться только по этой кривой.

Если переходный процесс описывается уравнением 2-го порядка, то в зависимости от н.у. изображающая точка может оказаться в любом месте фазовой плоскости.

Если процесс в цепи является периодическим, то через интервалы времени, равные периоду процесса, соответствующие друг другу значения и 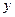повторяются, а фазовая траектория в этом случае будет замкнутой кривой. Замкнутая фазовая траектория называется предельным циклом. Если же процесс является непериодическим, то фазовая траектория представляет собой незамкнутую кривую.

Фазовую траекторию можно наблюдать на экране ЭЛО.

7.7 ИЗОБРАЖЕНИЕ ПРОСТЕЙШИХ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ НА ФАЗОВОЙ ПЛОСКОСТИ

Пример 7.1 Пусть цепь,содержащая r и L с начальным током 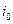, переключается без разрыва тока на источник постоянного напряжения U (рис. 7.2).

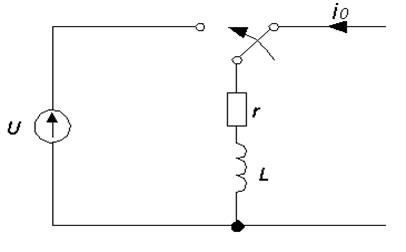
Рисунок 7.2

Переходный процесс в этой цепи описывается уравнением

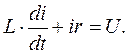(7.1)

Введя обозначения i(t)= x (t) и 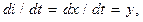получаем

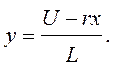(7.2)

Уравнение (7.2) – это уравнение прямой линии, проходящей через точки с координатами и 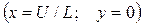- рис. 7.3

Рисунок 7.3

Для верхней полуплоскости 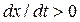и изображающая точка перемещается в направлении возрастающих значений . Для нижней полуплоскости 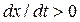и изображающая точка перемещается в направлении убывания значений . Точка равновесия А лежит на оси OX и соответствует установившемуся режиму.

В зависимости от начального значения тока 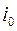( при t=0) фазовая траектория может начаться в различных точках прямой - в верхней или нижней полуплоскости. С течением времени (вне зависимости от н.у.) движение изображающей точки происходит в направлении т.А. Причем, скорость движения уменьшается по мере приближения к т.А.

Если указанная цепь r, L замыкается накоротко (U=0), то фазовая траектория проходит через начало координат .

Аналогичные фазовые траектории получаются и для переходных процессов в цепях r, C.

Пример 2. Фазовые траектории переходного процесса в цепи с r, L, C (рис. 7.4) сложнее.

Рисунок 7.4

а) Рассмотрим случай, когда 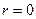, а и 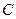соединены последовательно. Начальное значение тока в индуктивности 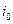и напряжения на емкости 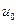могут быть любые. Диф. уравнение переходного процесса в этом случае имеет вид:

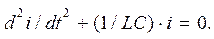
Действительно, согласно 2-му закону Кирхгофа можно записать, что

Известно, что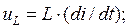

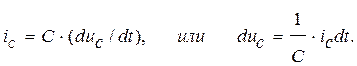
Интегрируя последнее, получаем 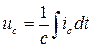. Подставив u_L и u_c в исходное уравнение, можно записать, что

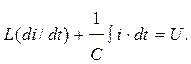
Продифференцировав обе части последнего уравнения, получаем:

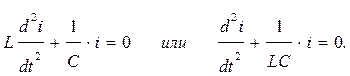
Введем обозначения: ,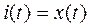

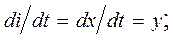
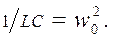
Тогда:

и

После интегрирования получаем: 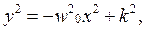где 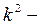постоянная интегрирования, зависящая от н.у. Последнее уравнение может быть записано в виде:

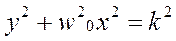или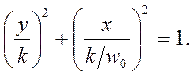

Данное уравнение на фазовой плоскости изображается семейством эллипсов (рис. 7.5а), вертикальные оси которых равны 2k, а горизонтальные - Полученные эллипсы соответствуют незатухающим гармоническим колебаниям. Амплитуда колебаний тока равна горизонтальной полуоси эллипса:

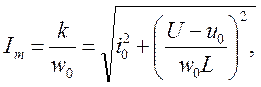
а частота w₀ – отношению вертикальной полуоси к горизонтальной.

б) В реальном колебательном контуре всегда есть некоторые потери и сопротивлением r нельзя пренебречь. За период колебаний амплитуда тока уменьшается и фазовые траектории имеют вид спиралей, завивающихся вокруг начала координат – рис. 7.5б.

в) По мере увеличения сопротивления r шаг спирали увеличивается и при семейство спиралей вырождается в семейство параболических кривых, проходящих через начало координат – рис. 7.5в.

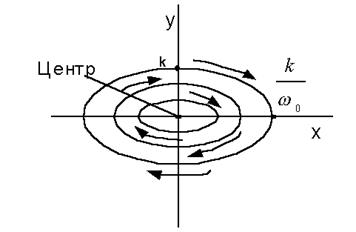
Рисунок 7.5а.

Рисунок 7.5б.

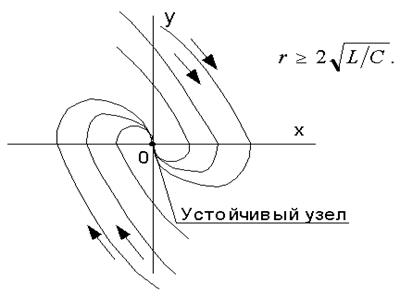
Рисунок 7.5в.

Сопоставляя фазовые траектории для 3-х различных значений r можно отметить некоторые общие свойства этих кривых:

1) все кривые пересекают ось ОХ под прямым углом с переменой знака производной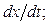

2) во всех 3-х случаях имеет место только одна точка устойчивого равновесия, лежащая в начале координат, но характер равновесия различный;

3) при r=0 равновесие наименее устойчивое и достаточно бесконечно малого отклонения от точки равновесия, чтобы начался незатухающий колебательный процесс с бесконечно малой амплитудой колебания; при этом изображающая точка совершает периодические движения по эллипсным орбитам с центром в точке равновесия; точка равновесия такого типа называется центром;

4) при 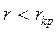все процессы, возникающие в цепи, носят затухающий колебательный характер; изображающая точка после любого принужденного отклонения от равновесия всегда возвращается в исходное положение равновесия, совершая несколько оборотов вокруг точки равновесия; такого рода точка равновесия называется устойчивым фокусом;

5) если 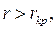то изображающая точка, возвращаясь апериодически в состояние равновесия, движется по параболе и не совершает более полуоборота вокруг начала координат; точка равновесия такого типа называется устойчивым узлом.

7.8 ИЗОКЛИНЫ. ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ КРИВЫХ

С ПОМОЩЬЮ ИЗОКЛИН

При построении фазовых траекторий процессов, описываемых диф. уравнениями 2-го порядка, удобно пользоваться методом изоклин.

Под изоклиной ( линией равного наклона) понимают геометрическое место точек фазовой плоскости, для которых производная есть некоторое постоянное число. Для одной изоклины, например, 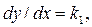для другой 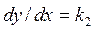и т.д.

Значение производной 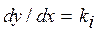равно угловому коэффициенту касательной, проведенной к любой интегральной кривой в точке ее пересечения с изоклиной, для которой

Выведем уравнение для построения семейства изоклин для линейной цепи, изображенной на рис. 7.4 (колебательный контур, подключенный к источнику U). Дифференциальное уравнение цепи имеет вид:

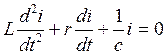. (1)

Действительно:

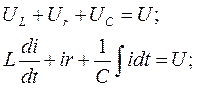
После дифференцирования получаем:

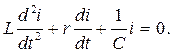
Вводим обозначения: i(t)=x(t); учитывая, что 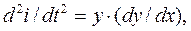после дифференцирования (7.3) получаем

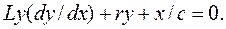(7.4)

Решая (7.4) относительно y получаем уравнение для построения семейства изоклин:

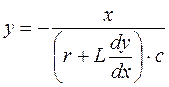. (7.5)

Для отыскания точек фазовой плоскости, принадлежащих первой изоклине, в уравнении (7.5) вместо 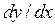подставляем 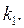Придаем x различные значения и из уравнения (7.5) при определяем соответствующие значения y. Совокупность полученных точек дает изоклину, для которой 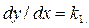. Полагая затем 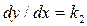строим таким же путем вторую изоклину и т.д.

Для линейных цепей изоклины будут прямыми линиями, проходящими через начало координат. Для нелинейных цепей изоклины в общем случае непрямые линии.

При графическом изображении изоклин на них наносят черточки (засечки). Черточки на изоклинах дают соответствующие углы, которые касательные образуют с осью OX.

После построения на фазовой плоскости семейства изоклин можно построить интегральные кривые. Допустим, надо построить интегральную кривую, т.е. зависимость y =f (x), проходящую через т. А, принадлежащую изоклине 1 (см. рис. 7.6).

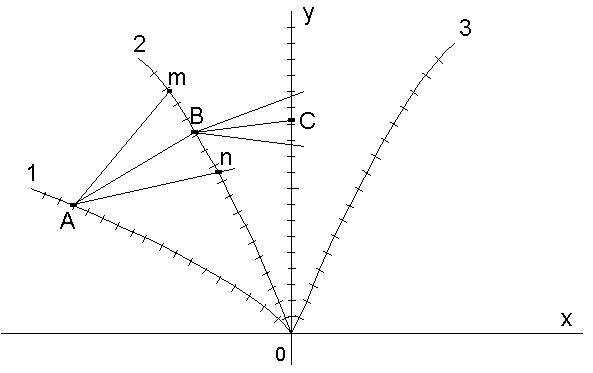
Рисунок 7.6

Порядок построений:

- из т. А проводим 2 луча до пересечения с изоклиной 2; первый проводим так, чтобы он составил с осью OХ, угол, тангенс которого равен 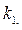т. е. угловому коэффициенту изоклины 1; этот луч пересекает изоклину 2 в точке m; второй луч проводим под углом, соответствующим изоклине 2; он пересекает изоклину 2 в точке n;

- делим расстояние mnпополам и получаем точку B; соединяем точку A и точкуB прямой – эта прямая и представляет собой кусочек интегральной кривой;

- далее проводим 2 луча из точки B до пересечения со следующей изоклиной (в данном случае – это ось OY) и получаем точку C. Отрезок BC представляет собой новый кусочек интегральной кривой. И т.д. Чем ближе будут расположены изоклины друг к другу, тем лучше, точнее ломаная линия будет соответствовать интегральной кривой.

Для нелинейных цепей семейство изоклин часто строят, заменяя характеристику нелинейного элемента отрезками прямых линий. В этом случае для каждого линейного участка на фазовой плоскости строят свое семейство изоклин. Каждое из этих семейств годится только для соответствующей области изменения x, граничные значения которого известны из характеристики нелинейного элемента.

7.9 УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ

Устойчивым предельным циклом называется предельный цикл, на который навиваются расположенные внутри и вне цикла близлежащие интегральные кривые. Физически он соответствует устойчивому периодическому процессу (линия 2 на рис. 7.7).

1 – неустойчивый предельный цикл;

2 – устойчивый предельный цикл.

Рисунок 7.7

Неустойчивым предельным называется такой предельный цикл, с которого раскручиваются (удаляются) вблизи расположенные интегральные кривые. Физически он соответствует неустойчивому процессу (линия 1 на рис. 7.7).

7.10 ПОСТРОЕНИЕ ВРЕМЕННЫХ ЗАВИСИМОСТЕЙ ПО

ЗАДАННОМУ ФАЗОВОМУ ИЗОБРАЖЕНИЮ

Пусть переходной процесс в нелинейной цепи описывается уравнением вида:

(7.6)

где u(t) – мгновенное напряжение на какой-либо ветви цепи, нелинейные коэффициенты, зависящие от u(t).

Для построения фазового изображения цепи введем обозначения:

u (t)= x (t);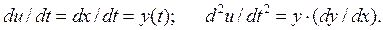

Тогда уравнение (7.6) можно записать в виде:

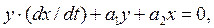
откуда уравнение изоклины будет иметь вид:

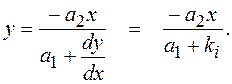(7.7)

Пусть с использованием уравнения (7.7) построено семейство изоклин, с помощью которого выполнено построение фазовой траектории цепи y= f (x, t), описываемой уравнением (7.6) – рис. 7.8.

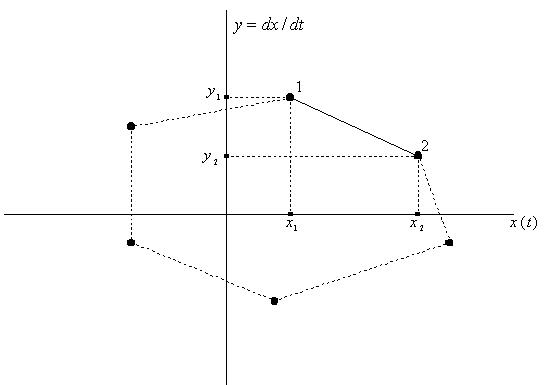
Рисунок 7.8

Для запишем уравнение отрезка траектории показанного замкнутого цикла:

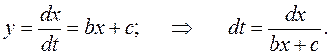
Интегрируя, получаем

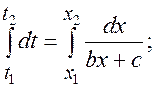
Из последнего выражения видно, что изменение переменной u(t) = x(t) на фазовой траектории от значения , до значения 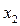произойдет за время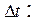

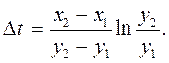
Определив время 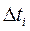для каждого отрезка фазовой траектории исследуемой цепи (рис. 7.8) можно построить график изменения во времени напряжения u(t), т. е. осциллограмму u(t).

7.11 КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ПРОЦЕССОВ

В НЕЛИНЕЙНЫХ ЦЕПЯХ ПРИ ПОМОЩИ ФАЗОВОЙ ПЛОСКОСТИ

Построения на фазовой плоскости могут проводиться с целью исследования:

а) устойчивости точек равновесия;

б) возможности возникновения автоколебаний в схеме;

в) устойчивости возникающих автоколебаний и определения их амплитуды;

г) влияния н.у. на возникающие в цепи процессы.

Допустим, что для некоторой цепи для мгновенных значений тока или напряжения построены интегральные кривые, соответствующие изображенным на рис. 7.7. Какие заключения можно сделать в отношении возможных переходных процессов в этой цепи при том значении параметров цепи, для которых эти кривые построены:

- в системе возможно лишь одно устойчивое состояние равновесия – начало координат;

- на фазовой плоскости есть один устойчивый предельный цикл (2) и один неустойчивый цикл (2);

- если н.у. в цепи таковы, что изображающая точка, характеризующая эти н.у., попадает внутрь неустойчивого предельного цикла ( кривой 1), то в системе возникает затухающий колебательный процесс, в результате которого цепь придет с течением времени в состояние устойчивого равновесия;

- если же н. у. таковы, что изображающая точка попадает в область, находящуюся снаружи кривой 1, то в результате переходных процессов в цепи возникнут устойчивые автоколебания – изображающая точка будет двигаться по устойчивому предельному циклу-кривой 2.

Таким образом, можно сказать, что в цепи будет либо устойчивое "в малом" состояние равновесия, либо будет устойчивый автоколебательный процесс. Какой из этих режимов возникает в цепи, все зависит от н. у.

С помощью фазовой плоскости при исследовании нелинейных систем (цепей), находящихся под воздействием периодической возмущающей силы, можно решить следующие вопросы:

- исследование влияния н.у. на характер установившегося или квазиустановившегося процесса;

- исследование устойчивости субгармонических^* колебаний и резонансов на высших гармониках;

- исследование устойчивости процессов автомодуляции.

В указанном случае построения на фазовой плоскости производят для медленно меняющихся величин или для огибающих амплитуд.

^* Под субгармоническими понимают колебания, частота которых меньше частоты периодической вынуждающей силы, действующей на систему.