Квантовые числа электронов

Строение атома. Двойственная природа электрона. Строение элект­ронных оболочек атомов. Квантовые числа. Атомные орбитали. Электрон­ные конфигурации атомов в основ­ном и возбужденном состояниях, принцип Паули, правило Гунда

Теория Бора

Модель строения атома, предложенная Резерфордом, подра­зумевала, что электрон — сугубо материальная частица, имею­щая массу и заряд и подчиняющаяся законам классической фи­зики. Но уже в самой модели были заложены противоречия с этими законами, т.к. в классической физике невозможно безызлучательное движение заряженной частицы.

Первым шагом для преодоления этих противоречий стала мо­дель Н. Бора, основывавшаяся также на законах классической физики, но с привлечением представлений новой в те времена, но интенсивно развивающейся науки — квантовой механики.

Для построения своей модели атома Бор ввел два постулата, согласно которым

1) Движение электрона вокруг ядра происходит по так называе­мым стационарным орбитам и описывается уравнением:

mvr=nh/2p

где т — масса электрона, v — его скорость, r — радиус стацио­нарной орбиты, n — натуральное число, соответствующее но­меру орбиты, a h — константа, называемая постоянной План­ка, h=6,62•10^-34 Дж•с.

2) Движение электрона по стационарной орбите происходит без излучения и поглощения энергии.

Каждой стационарной орбите соответствует определенное энергетическое состояние электрона. Электрон может переходить с одной стационарной орбиты на другую, но это требует поглоще­ния или испускания порции (кванта) энергии. Переход электрона с орбиты с номером n, которой соответствует состояние с энергией e_n, на орбиту с номером k (состояние с энергией e_k) требует погло­щения (n<k) или испускания (n>k) энергии De_nk, равной

по абсолютной величине разности энергий соответствующих со­стояний:

De_nk=e_n-e_k. Поскольку

Е=hv,

где v — частота излучения, то

De_nk =h(n_n- n_k) = hn_nk,

где n_nk соответствует частоте того кванта энергии, который был поглощен или испущен электроном в процессе перехода с одной стационарной орбиты на другую.

Развитие квантовой механики изменило взгляды ученых на электрон. Оказалось, что ему присущ корпускулярно-волновой дуализм. Это значит, что электрон проявляет свойства как обыч­ной частицы (имеет массу и заряд), так и свойства волны (способ­ность к дифракции и интерференции). Квантовая механика опе­рирует сложнейшим математическим аппаратом, мы же остановимся лишь на некоторых выводах, необходимых для по­нимания строения атома и образования химической связи. Основ­ной характеристикой волны является длина Д. Для электрона с массой т и скоростью v длина волны определяется соотношением де Бройля:

l=h/mv

Из дуалистичной природы электрона следует принцип не­определенности Гейзенберга, который постулирует невозмож­ность одновременного точного определения местонахождения электрона и его скорости. Математически это выражается соот­ношением:

Dх•Dv>h/4pm

Dх — погрешность координаты, Dv — погрешность скорости, т — масса электрона. Физический смысл принципа неопределенности заключается в том, что чем с большей точностью мы знаем место­нахождение электрона (координату), тем меньше точность в опре­делении его скорости в данный момент времени.

Согласно принципам квантовой механики движение электро­на в атоме не описывается уравнением Бора для орбиты. Электрон может находиться в любой точке пространства около ядра, но с разной вероятностью. Поэтому говорят об электронной плотности как о вероятности обнаружить электрон в какой-либо точке. С

понятием электронной плотности связано определение электрон­ного облака, т.е. области пространства, внутри которой электрон­ная плотность велика (вероятность более 90% ). Электронные об­лака имеют различную форму, которая определяется характером движения электрона около ядра. Характер движения электрона называется орбиталью. Орбиталь является больше энергетичес­ким параметром, нежели пространственным.

Квантовые числа электронов

Квантовая теория подразумевает, что энергия электрона может принимать только определенные значения, т.е. квантует­ся. Энергия электрона, форма электронного облака и другие пара­метры описывают состояние электрона в атоме. Состояние элек­трона характеризуется совокупностью чисел, называемых квантовыми числами.

Главное квантовое число n служит для отнесения состояния электрона к тому или иному энергетическому уровню, под кото­рым понимается набор орбиталей с близкими значениями энер­гии. Главное квантовое число может принимать любое значение из области натуральных чисел, т.е.n=1, 2, 3. При переходе элек­трона с одного энергетического уровня на другой главное кванто­вое число изменяется. (Можно сопоставить с переходом электрона с одной стационарной орбиты на другую в модели Бора.)

Энергетический уровень включает в себя несколько орбита­лей. Орбитали с одинаковой энергией, принадлежащие одному энергетическому уровню, образуют энергетический подуровень. Отнесение орбитали к какому-либо подуровню производится при помощи побочного (орбитального) квантового числа l. Оно может принимать целочисленные значения от 0 до n-1. Т.е. для электрона с главным квантовым числом n орбитальное квантовое число l может принимать n значений от l=0 до l=n-1.Так, при n=1, l=0; при n=2, l=0 и l=1, при n=3, l=0, 1, 2. Число l входит в выражение для момента импульса электрона при его движении вокруг ядра:

p=hÖ(l((l+1))

Орбитальное квантовое число показывает, какому подуровню данного энергетического уровня соответствует характер движе­ния рассматриваемого электрона. Очень часто состояния электро­на обозначают латинскими буквами, при этом состояние с l=0 называют s-орбиталью, l=1 — р-орбиталью, l=2 — d-орбиталью l=3 — f-орбиталью, l=4 — g-орбиталью и т.д.

Электронные облака орбиталей с разными значениями l имеют разную конфигурацию, а с одинаковыми l похожую. Так,

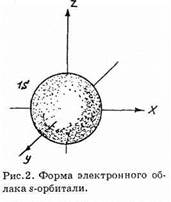
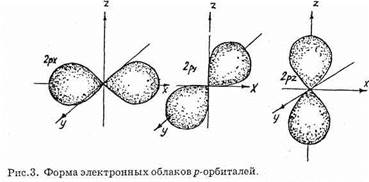
при l=0 (s-орбиталь) для электрона с любым значением главного кван­тового числа n электронное облако ограничено сферой (рис. 2), и чем больше n, тем больше ее радиус. Электронные облака p-орбиталей (l=1) имеют форму «вращающейся восьмерки» (рис. 3). При увеличе­нии значения числа l формы элек­тронных облаков усложняются. Соответственно увеличивается энергия электрона, который зани­мает данную орбиталь.

Как видно из рисунка 3, орби­тальному квантовому числу l=1 соответствуют три различным образом ориентированных в про­странстве, но одинаковых по форме электронных облака (они называются р_x, р_y, р_z-орбитали в соответствии с их расположением в пространстве). Вообще, на подуровне с орбитальным числом l на­ходится 2l+1 орбиталь с одинаковой энергией.

Для того, чтобы различать электроны, занимающие одинако­вые по энергии орбитали, введено магнитное квантовое число m_l. Его квантово-механический смысл в том, что m_l выражает проек­цию орбитального момента импульса на направление магнитного поля. Именно магнитное квантовое число отражает пространст­венную ориентацию орбиталей с одинаковым числом l. Соответ­ственно, для электрона с орбитальным квантовым числом l воз­можны 2l+1 различных значений магнитного квантового числа m_l, от -l до +l, включая 0. Это значит, что, например, на третьем энергетическом уровне (n=3, l=0,1,2), при l=2 (d-подуровень)

электрон может находиться на 2 • 2 + 1 = 5 различных орбиталях с одинаковой энергией.

Четвертое квантовое число называется магнитным спино­вым числом m_s (или просто спином s) и характеризует чисто кван­товое свойство электрона — спин. Спин электрона есть собствен­ный момент количества движения. Хотя интерпретация этого свойства сложна, его можно уподобить вращению электрона во­круг своей воображаемой оси. Магнитное спиновое число m_s может быть равно либо (-1/2), либо (+1/2)¹.

Электронные конфигурации атомов

Итак, атом состоит из ядра и электронов, определенным обра­зом распределенных в околоядерном пространстве. При этом электроны находятся на некотором конечном расстоянии от ядра. Между ядром (положительный заряд) и электронами (заряжены отрицательно) действуют силы электростатической природы . Поэтому чем меньше расстояние между электроном и ядром, тем больше энергия взаимодействия между ними. Поскольку полную энергию электрона определить чрезвычайно сложно, то услови­лись считать, что его потенциальная энергия равна нулю, если электрон бесконечно удален от ядра. Используя это состояние как начало отсчета, определяют относительную энергию электрона.

Электроны образуют электронную оболочку атома. Электрон­ная оболочка представляет собой набор энергетических уровней. Принадлежность электрона к какому-либо энергетическому уровню определяется главным квантовым числом п. Вообще, атом содержит бесконечно много энергетических уровней (n=1, 2, 3,...), но не все из них заполнены электронами. При заполнении электронной оболочки атома выполняется принцип наименьшей энергии, т.е.

¹ Вообще, абсолютное значение спина для любого электрона равно S=1/2, а число m_s обозначает проекцию спина на ось г. Иногда число S тоже включают в набор квантовых чисел.

² По закону Кулона сила взаимодействия двух зарядов пропорциональна произве­дению зарядов и обратно пропорциональна квадрату расстояния между ними.

Именно основные состояния мы будем иметь в виду при рас­смотрении заполнения электронных оболочек атомов.

Согласно принципу наименьшей энергии, сначала заполняет­ся энергетический уровень с n=1, затем, после заполнения пер­вого уровня, с n=2 и т.д. Всего на первом уровне (n=1) может находиться только два электрона, на втором (n=2) восемь, на третьем (га = 3) восемнадцать, т.е. на уровне с номером n может находиться не более 2n² электронов. Это следует из другого пра­вила, которое выполняется при построении электронной оболоч­ки атома и называется принципом Паули.

Поэтому на первом уровне (n=1,l=n-1=0, орбиталь s-типа) электроны могут различаться только значением спинового числа n_s, а поскольку для него возможны только два значения (-1/2 и +1/2), то первый энергетический уровень может быть занят не более чем двумя электронами. Заполнение этого уровня происхо­дит в невозбужденных атомах водорода и гелия. Схематично это можно представить следующим образом:

Клеточка обозначает орбиталь, а стрелки — электроны, при этом направление стрелки указывает спин. Если две стрелки имеют одинаковое направление, то это значит, что эти два элек­трона имеют одинаковые спины (магнитное спиновое число m_s для обоих электронов имеет значение либо -1/2, либо +1/2). Раз­нонаправленными стрелками обозначают электроны, у одного из которых m_s=-1/2, а у другого ms = +1/2. Символами 1s¹ и 1s² обозначена электронная конфигурация атомов, которая показы­вает, что в атоме водорода единственный электрон занимает 1s-орбиталь, а в атоме гелия на 1s-орбитали располагаются два элек­трона.

Когда мы переходим на второй электронный уровень (главное квантовое число 2), или, что то же самое, к элементам второго периода, появляется возможность размещения электронов не

только на s , но и на р -орбиталях (квантовое число 1 может прини­мать значение 0 и 1). Электронные оболочки лития и бериллия заполняются так же, как для водорода и гелия

В атоме бора появляется первый электрон на р-орбитали.

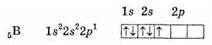
Следующий электрон (в атоме углерода) можно разместить на той же p_x-орбитали (его спин будет противоположным, и принцип Паули не будет нарушен), но можно и на другой (p_y-орбиталь), поскольку их энергия одинакова. Реально в атоме углерода элек­трон размещается именно на p_y-орбитали. Размещение электро­нов на орбиталях с одинаковой энергией определяется правилом Гунда:

Это правило можно переформулировать по другому — на ор­биталях с одинаковой энергией электроны размещаются так, чтобы имелось максимальное число неспаренных электронов. В соответствии с этим правилом в атоме углерода и в атомах следу­ющих элементов второго периода:

При переходе к третьему уровню (к элементам третьего перио­да) появляются три типа орбиталей s, p, и d-орбитали. Заполнение орбиталей первых восьми элементов происходит так же, как в случае второго периода. Далее можно было бы ожидать заполне-

ния d-орбиталей, однако после аргона (как видно из таблицы Менделеева) появляется калий — элемент четвертого периода. Почему? Энергия электрона на орбитали определяется (что оче­видно из ранее сказанного) как главным квантовым числом n, так и побочным l. Соответственно работает следствие из принципа наименьшей энергии, называемое правилом Клечковского:

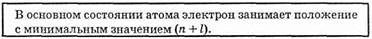
Если бы в атоме калия последний электрон занял 3d-орбиталь, то значение указанной суммы было бы 3(n=3)+2(l=2)=5, но он занимает 4s-орбиталь, и сумма составляет 4(n=4)+0(l=0) = 4. То же происходит со следующим электроном в атоме кальция. Однако далее более выгодным становится заполнение 3d-орбиталей, и атом скандия открывает ряд переходных элементов 4-го периода, в которых заполняются 10 вакансий Sd-орбиталей. Схема заполнения орбиталей отражена на рис. 4.

Правило Клечковского не абсолютно, так как не учитывает, что спаренные электроны имеют большую энергию, чем неспарен­ные (что составляет основу правила Гунда). Так, в атоме хрома, кроме появления очередного электрона на 3d-орбитали, на ту же орбиталь переходит один из 4s-электронов (так называемый «про­скок электрона»). В следующем атоме марганца этот электрон возвращается обратно.

Напоминаем, что все сказанное относится к основному состо­янию атома. В возбужденном состоянии (когда атому придана дополнительная энергия) работает только принцип Паули.

Используя изложенные выше правила, вы всегда сможете составить электронную формулу любого элемента в его основном состоянии.

Электронные формулы

Распределение электронов в атоме по энергетическим уров­ням и подуровням изображают в виде электронных формул. Рас­смотрим, как они составляются.

Напоминаем! Каждый электрон в атоме занимает свободную орбиталь с наиболее низкой энергией, отвечающей его прочной связи с ядром, — принцип наименьшей энергии. С ростом поряд­кового номера элемента электроны заполняют орбитали и уровни в порядке возрастания их энергии, а подуровни — в последова­тельности s-p-d-f. Последовательность возрастания энергии на­зывается шкалой энергии. В соответствии с ней составляют ряд последовательного заполнения электронами орбиталей атомов

Рис.4. Схема заполнения электронами энергетических уровней и поду­ровней.

элементов периодической системы. Этот ряд, в котором верти­кальными линейками отделены периоды, обозначенные сверху цифрами, имеет вид (см. рис, 4).

Орбиталь с минимальной энергией — это 1s-орбиталь. У атома водорода она занята его единственным электроном. Поэтому элек­тронная формула (или электронная конфигурация) атома водоро­да имеет вид:

Так как на одной орбитали могут находиться два электрона, то оба электрона атома гелия размещаются на 1s-орбитали. Сле-

довательно, электронная формула атома гелия 1s² . Электронная оболочка Не завершена и очень устойчива, это благородный газ.

У атомов элементов второго периода заполняется L-уровень (n=2), причем вначале орбиталь s-подуровня, а затем три орби­тали р-подуровня. Электронная формула атома лития ₃Li: 1s²2s¹ Электрон 2s¹ намного слабее связан с ядром атома, чем 1s-электроны, поэтому атом лития может легко терять его, образуя ион Li⁺.

В атоме ₄Ве четвертый электрон также размещается на 2s-орбитали: 1s²2s². Легче других электронов у Be отрываются два 2s-электрона с образованием иона Ве²⁺

Поскольку 2s-орбиталь заполнена, то пятый электрон у атома бора ₅В занимает 2р-орбиталь. Электронная формула атома бора ₅В: 1s²2s²p¹.

Далее у атомов С, N, О, F идет заполнение 2р-орбиталей, кото­рое заканчивается у атома Ne (см. стр. 30).

Начиная с элементов третьего периода у атомов идет заполне­ние третьего М-уровня, состоящего из 3s-, Зр- и Зd-подуровней.

Например: ₁₁Na: 1s²2s²2p⁶3s¹

_]7Сl: 1s²2s²2p⁶3s²3p⁵

Иногда в формулах, изображающих распределение электро­нов в атомах, указывают только число электронов на каждом энергетическом уровне. Тогда их записывают так:

₁₁Na = 2. 8. 1; ₁₇Сl — 2. 8. 7; ₂₆Fe —2. 8.14. 2.

При написании электронных формул следует учитывать так называемый «проскок» электрона. Так, электронная формула хрома должна быть 1s²2s²2p⁶3s²3p⁶3d⁴4s². Однако на внешнем уровне у атома хрома не два электрона, а один: второй электрон « проскочил » на d-подуровень второго снаружи уровня (см. Прин­цип наименьшей энергии). В таком случае расположение электро­нов у атома хрома такое: 1s²2s²2p⁶3s²3p⁶3d⁵4s¹. To же имеет место у Nb, Mo и других элементов. У Pd электроны по уровням распо­лагаются так: 2. 8. 18. 18. 0 (здесь пятый энергетический уровень вообще отсутствует: оба электрона «проскочили» на соседний уро­вень).

Часто структуру электронных оболочек изображают с помо­щью энергетических, или квантовых, ячеек — это так называе­мые графические электронные формулы (ячейки Гунда).

В качестве примера рассмотрим схему распределения элек­тронов по квантовым ячейкам в атоме углерода:

(возбужденное, неустойчивое состояние)

Напоминаем!

Орбитали подуровня заполняются так: сначала по одному электрону с одинаковыми спинами, а затем по второму электрону с противоположными спинами. Поскольку в 2р-подуровне три орбитали с одинаковой энергией, то каждый из двух 2р-электро-нов занял по одной орбитали (например, р_х, р_у). Одна орбиталь осталась свободной (р_z). У атома углерода в устойчивом состоянии два неспаренных электрона. В возбужденном атоме углерода че­тыре неспаренных электрона. Слева от схем — в электронных формулах даны более подробные записи с указанием расположе­ния электронов на р_x-p_y-p_z-орбиталях. Эту запись тоже часто при­меняют.

Часто постоянную Планка обозначают ћ=h/2p=1,05•10^-34 Дж•c

Неважно, какому направлению стрелки соответствует спин -1/2, а какому +1/2. Главное, чтобы электроны с одинаковыми спинами обозначались одинаковыми стрелками