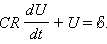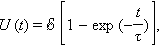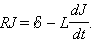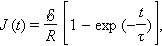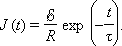Квазистационарные процессы. RC- и RL-цепи

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ

Колебательные и волновые процессы, изучаемые в различных разделах физики, проявляют удивительную общность закономерностей. Колебания груза на пружине и процессы в электрическом колебательном контуре, колебания столба воздуха в органной трубе и ход механических часов, распространение света и звуковых волн и т. д. – все эти явления протекают очень похожим образом. Однако они имеют различную физическую природу. Чтобы решить, например, задачу о колебаниях груза на пружине, нужно знать законы Ньютона, решение задачи о колебаниях в электрическом контуре требует знания законов электродинамики. Но математические уравнения, описывающие процессы, происходящие в этих двух системах, оказываются одинаковыми. Аналогично обстоит дело и с волновыми процессами.

Общность колебательных и волновых закономерностей проявляется в общности математических уравнений, описывающих процессы различной физической природы.

Квазистационарные процессы. RC- и RL-цепи

В цепях постоянного тока распределение электрических зарядов на проводниках и токов на участках цепи стационарно, то есть неизменно во времени. Электромагнитное поле в таких цепях состоит из электростатического поля неподвижных зарядов и магнитного поля постоянных токов. Эти поля существуют независимо друг от друга.

Если на каком-то участке цепи происходят изменения силы тока или напряжения, то другие участки цепи могут «почувствовать» эти изменения только через некоторое время, которое по порядку величины равно времени τ распространения электромагнитного возмущения от одной точки цепи к другой. Так как электромагнитные возмущения распространяются с конечной скоростью, равной скорости света c , то 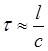, где l – расстояние между наиболее удаленными точками цепи. Если время τ много меньше длительности процессов, происходящих в цепи, то можно считать, что в каждый момент времени сила тока одинакова во всех последовательно соединенных участках цепи. Процессы такого рода в электрических цепях, а также сами цепи, называются квазистационарными.

Квазистационарные процессы можно исследовать с помощью законов постоянного тока, если применять эти законы к мгновенным значениям сил токов и напряжений на участках цепи.

Из-за огромного значения скорости света время установления в цепи электрического равновесия оказывается весьма малым. Поэтому к квазистационарным можно отнести многие достаточно быстрые в обычном смысле процессы. Например, быстрые колебания в радиотехнических цепях с частотами порядка миллиона колебаний в секунду и даже выше очень часто еще можно рассматривать как квазистационарные.

Простыми примерами квазистационарных процессов могут служить процессы, происходящие в RC- и RL-цепях при подключении и отключении источника постоянного тока.

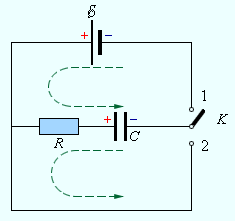
На рис. 1 изображена электрическая цепь, состоящая из конденсатора емкостью C, резистора сопротивлением R и источника тока с ЭДС, равной ε.

Рис. 1. Цепи зарядки и разрядки конденсатора через резистор

Если замкнуть ключ K в положение 1, то начинается процесс зарядки конденсатора через резистор. Для квазистационарной цепи по закону Ома можно записать:

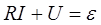
где I – мгновенное значение силы тока в цепи, U – мгновенное значение напряжения на конденсаторе. Сила тока I в цепи равна изменению заряда q конденсатора в единицу времени: 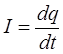. Напряжение U на конденсаторе в любой момент времени равно 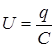. Из этих соотношений следует

Мы получили дифференциальное уравнение, описывающее процесс зарядки конденсатора. Если конденсатор вначале не был заряжен, то решение этого уравнения имеет вид

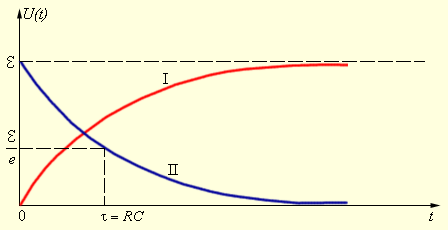
где τ = RC – так называемая постоянная времени цепи, состоящей из резистора и конденсатора. Величина τ является характеристикой скорости процесса. При t → ∞, U (t) → ε.

Процесс зарядки конденсатора через резистор изображен на рис. 2 (I).

Рис. 2. Зарядка (I) и разрядка (II) конденсатора через резистор

Если после того, как конденсатор полностью зарядился до напряжения ε, ключ K переключить в положение 2, то начнется процесс разрядки.

Внешний источник тока в цепи разрядки отсутствует (ε = 0). Процесс разрядки описывается выражением

U (t) = exp (–t / τ).

Зависимость U (t) в процессе разрядки изображена на рис. 2 (II). При t = τ напряжение на конденсаторе уменьшается в e ≈ 2,7 раз.

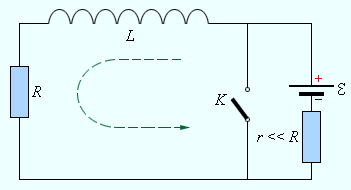
Аналогично протекают процессы в цепи, содержащей катушку с индуктивностью L и резистор сопротивлением R (рис.3).

Рис. 3.

Цепь, содержащая катушку индуктивностью L, резистор сопротивлением R

и источник тока с ЭДС, равной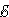

Если в цепи, изображенной на рис. 3, ключ K сначала был замкнут, а затем внезапно разомкнут, то начнется процесс установления тока. В схему последовательно с источником тока включен резистор r с малым сопротивлением, чтобы при замкнутом ключе K батарея не оказалась закороченной. Поскольку r << R, при написании уравнения для процесса установления тока этим сопротивлением можно пренебречь. Этот процесс описывается уравнением

Это уравнение по виду совпадает с уравнением, описывающим зарядку конденсатора, только теперь переменной величиной является сила тока I. Решение этого уравнения имеет вид

где постоянная времени τ = L / R. Аналогичным образом можно получить закон убывания тока в RL-цепи после замыкания ключа K:

Следует отметить, что процессы в RC- и RL-цепях аналогичны механическим процессам при движении тела в вязкой жидкости.