УРАВНЕНИЙ ИХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Под математической моделью схемы электронной (электрической) цепи понимают отображение (в соответствии с физическими законами и требуемой точностью) процессов, протекающих в цепи, посредством математических представлений (формул, уравнений и др. математических образов). Модель создаётся для определения необходимых характеристик и параметров цепи.

Как правило, выбор модели осуществляется на основании учёта достаточно противоречивых факторов. Чем сложнее реальный объект, чем точнее и глубже необходимо провести его исследование, тем сложнее в общем случае оказывается модель. Но сложное описание объекта затрудняет в свою очередь работу с моделью. Разрешение этого противоречия требует известного искусства в выборе допустимого уровня абстракции при отбрасывании всех не существенных факторов.

В общем случае зависимости между токами и напряжениями на выводах реальной цепи достаточно сложны, как правило – нелинейные и носят в определённой степени статистический (вероятностный) характер. Однако, при работе цепи в стационарных условиях статистический характер её параметров может быть выражен слабо и его можно часто не учитывать; степень нелинейности характеристик цепи может быть различной в зависимости от режима работы и влияний внешних воздействий; поэтому при формировании математической модели в зависимости от цели анализа и требуемой точности допустимо заменить нелинейные зависимости линейными; в результате точная и сложная нелинейная модель может быть заменена менее точной, но более простой линейной моделью.

Обычно математические модели, используемые в анализе электронных схем, имеют вид дифференциальных или алгебраических уравнений (или систем уравнений). Традиционно сложилась следующая классификация электронных схем в зависимости от типа уравнений, составляющих их математические модели: линейные схемы, линейные параметрические схемы, нелинейные схемы, нелинейно-параметрические схемы.

Линейные схемы. Параметры всех компонентов линейной схемы можно считать постоянными. Такие схемы описывают алгебраические или дифференциальные уравнения с постоянными коэффициентами. К моделям линейных схем применим метод наложения.

Формулировка принципа наложения: реакция линейной системы на действие суммы возмущений равна сумме реакций на действие каждого возмущения в отдельности.

Важное свойство линейных схем: реакции линейных схем с постоянными параметрами не содержат новых спектральных составляющих по отношению к спектрам воздействующих на схему сигналов.

К разряду линейных относят:

- схемы, составленные из линейных компонентов, токи и напряжения на полюсах которых всегда связаны между собой линейными зависимостями (пассивные компоненты);

- схемы, содержащие квазилинейные компоненты (лампы, транзисторы, операционные усилители, оптроны и т.д.), зависимости между токами и напряжениями на полюсах которых с определёнными допущениями могут быть описаны линейными соотношениями. Как правило, такое возможно при работе схем в режиме малого сигнала. Причём, чем меньше размах переменных сигналов (токов и напряжений) в схеме, тем ближе режим её работы к линейному.

Линейные методы анализа находят широкое применение, т.к. целый ряд электронных устройств работает в линейном режиме (линейные усилители, линейные преобразователи и т.д.). Кроме того, целый ряд импульсных устройств на некоторых временных интервалах можно рассматривать как линейные.

Линейные параметрические схемы. Это схемы, содержащие компоненты с изменяющимися во времени параметрами под действием дополнительного управляющего источника. Такие схемы описываются линейными уравнениями с изменяющимися во времени коэффициентами. При анализе таких схем может быть применён принцип наложения.

Однако в отличии от линейных схем с постоянными параметрами, в выходном сигнале линейных параметрических схем возникают новые спектральные составляющие при воздействии на входе схемы гармонического сигнала и при изменении во времени её параметров.

Пример линейной параметрической схемы: схема, содержащая источник питания, последовательно с которым включён угольный микрофон, сопротивление которого меняется под действием звукового давления.

Нелинейные схемы. Содержат хотя бы один компонент, токи и напряжения на полюсах которого связаны нелинейной зависимостью. Такие схемы описывают с помощью нелинейных уравнений, т.е. уравнений, в которых отдельные коэффициенты при переменных не являются постоянными, а зависят от самой переменной или её производных. Принцип наложения при анализе нелинейных схем неприменим.

Важным свойством нелинейных схем, на котором основано их многочисленное применение, является появление в реакции схем новых спектральных составляющих относительно спектрального состава входного воздействия.

Нелинейно-параметрические схемы. Это схемы, содержащие нелинейные компоненты и компоненты с переменными во времени параметрами. Описывают такие схемы нелинейные уравнения с переменными во времени коэффициентами.

1.5 МЕТОДЫ РАСЧЁТА ЦЕПЕЙ, СОДЕРЖАЩИХ НЕЛИНЕЙНЫЕ

ЭЛЕМЕНТЫ

Зависимости между токами и напряжениями на полюсах электронной цепи в общем случае всегда не линейны. Это обусловлено тем, что применяемые в них электронные и полупроводниковые приборы являются нелинейными сопротивлениями. Расчёт цепей с такими сопротивлениями представляет определённые трудности, т.к. величина нелинейного сопротивления изменяется с изменением проходящего через него тока или приложенного к нему напряжения. Закон изменения сопротивления определяется в.а.х. элемента и без знания этого закона невозможно рассчитать цепь.

Методы расчёта электронных (электрических) цепей, основанные на использовании в.а.х., заданной в виде графика, называют графическими.

Если в.а.х. с достаточной для практики точностью можно выразить аналитически в виде функциональной зависимости между I и U, то можно применять аналитические методы расчёта.

Графический метод расчёта основан на использовании широко известного способа графического решения систем уравнений. Его достоинство – наглядность и простота.

Аналитический метод расчёта требует предварительной аппроксимации нелинейной в.а.х. математической зависимостью I=f(U). точность расчёта аналитическим методом определяется точностью аппроксимации. Повышение точности аппроксимации приводит к усложнению формул и повышает сложность и трудоёмкость расчёта. Оба метода – графический и аналитический – являются приближёнными.

Широко применяю также графоаналитический метод, сочетающий приёмы графического и аналитического методов. Он обеспечивает достаточную точность расчёта и не очень сложен. Сущность этого метода заключается в том, что решается система уравнений, часть которых задана аналитически, а часть – графически. Решение ведётся в основном графическим методом с проведением некоторых промежуточных расчётов. Достоинства метода: наглядность; меньший, по сравнению с аналитическим методом, объём вычислительных работ; нет необходимости осуществлять аппроксимацию в.а.х..

Необходимые в.а.х. нелинейных элементов даются в справочной литературе. Однако надо иметь в виду, что в литературе приводят усреднённые характеристики, отличающиеся от реальных тем больше, чем шире поле допуска на основные параметры элемента. Наибольшая точность расчёта графическим или графоаналитическим методом достигается при использовании в.а.х., полученных экспериментально.

1.6 АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ В.А.Х. НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ

Аналитическое представление характеристик, заданных в виде графиков или таблиц, возможно только приближённо. Как правило, чем выше требуемая точность представления, тем сложнее получается аналитическое выражение, тем труднее решение уравнений, полученных на основе этого выражения. Поэтому необходим компромисс между сложностью аппроксимирующей функции и точностью приближения.

Следует отметить, что выполняя аналитическую аппроксимацию характеристик, заданных графически или в виде таблиц, приходится решать 2 основных вопроса: а) выбор аппроксимирующей функции; б) получение требуемой точности приближения (аппроксимации).

В качестве аппроксимирующих принимают различные функции: степенные полиномы, экспоненциальные полиномы, некоторые трансцендентные функции, кусочно-линейные функции. На выбор той или иной функции влияет вид конкретной характеристики. Наиболее часто при аппроксимации используются степенные алгебраические полиномы одной переменной вида

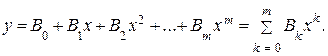
или кусочно-линейные функции. Из трансцендентных функций находят применение гиперболический синус и гиперболический тангенс (их недостаток – сложность определения их коэффициентов из условия приближения).

Степенное приближение. Неизвестные коэффициенты В_к степенного полинома (их количество равно m+1) могут быть определены из условия: погрешность, равная отклонению полинома y=j(x) от подлежащей аппроксимации характеристики f(x), не должна превышать некоторую заданную величину. При этом предельно допустимая погрешность должна задаваться с учётом требования точности расчётов, возможного разброса и нестабильности характеристик, а так же точности их экспериментального определения.

Для определения коэффициентов В_к аппроксимирующего полинома применяется несколько методов, основные из которых:

а) графический метод;

б) метод интерполяционных формул;

в) метод средних;

г) метод наименьших квадратов.

Кусочно-линейное приближение (аппроксимация). Кусочно-линейное приближение основано на замене отдельных участков аппроксимирующей характеристики отрезками прямых. Такая замена может быть осуществлена с помощью несложных графических построений. Точность аппроксимации зависит от числа интервалов линейного приближения в заданном интервале. При заданной погрешности приближения (аппроксимации) количество отрезков зависит от вида аппроксимирующей характеристики. Конечно, для упрощения расчётов с применением полученного приближения желательно иметь минимальное число линейных отрезков (интервалов).

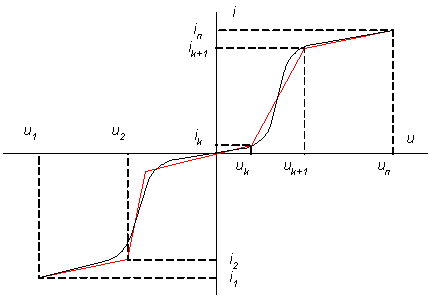
Рисунок 1.1

Получаемое кусочно-линейное приближение аппроксимируемой характеристики определяется координатами точек излома (u_k ,i_k), определяющих границы между смежными интервалами, и уравнениями отрезков прямых между соседними точками излома (u_k ,i_k) и (u_{k +1} ,i_k+1). Уравнение отрезка прямой к-го линейного участка между точками излома (u_k ,i_k) и (u_{k +1} ,i_k+1) можно записать в виде:

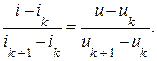
(1.1)

После несложных преобразований получаем:

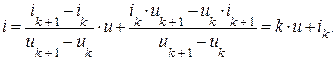
(1.2)

]Здесь: к – угловой коэффициент отрезка прямой; i_k – ордината точки пересечения прямой с осью “i”; u, i – текущие координаты точки на отрезке прямой.

Если решить (1.1) относительно напряжения “u”, то получим:

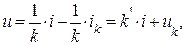
(1.3)

где к^’=1/к – угловой коэффициент прямой;

u_k – абсцисса точки пересечения прямой с осью “u”.

Достоинства кусочно-линейного приближения:

1) на каждом отрезке нелинейный элемент можно рассматривать как линейный и для анализа такой линеаризованной цепи применять аппарат теории линейных цепей;

2) на основе кусочно-линейного приближения можно составить относительно простые приближённые линейные схемы замещения различных элементов и цепей с нелинейными характеристиками.

1.7 СИНТЕЗ СХЕМ, РЕАЛИЗУЮЩИХ ТРЕБУЕМЫЕ В.А.Х.

При проектировании некоторых электронных устройств необходимо получать заданные в.а.х. с помощью комбинации (соединения) простейших элементов. Речь идёт о конструировании цепи (схемы) с требуемой в.а.х.. эта задача является задачей синтеза нелинейного резистивного двухполюсника с заданной в.а.х..

Общий порядок решения данной задачи сводится к:

а) кусочно-линейной аппроксимации заданной в.а.х.;

б) технической реализации аппроксимирующей характеристики двухполюсным блоком, составленным из простейших элементов, имеющих в.а.х., близкую к кусочно-линейной.

Элементарный блок, входящий в состав создаваемой цепи и реализующий участок заданной в.а.х., должен иметь простейшую кусочно-линейную в.а.х. с двумя линейными участками и регулируемыми параметрами – координаты точки излома и угла между линейными отрезками.

Требования к элементам, используемым в блоках:

а) в.а.х. элементов должны быть близки к идеализированным (с прямолинейными участками), чтобы их соединение могло дать простейшую кусочно-линейную характеристику;

б) параметры элементов должны позволять легко регулировать параметры простейших характеристик;

в) элементы должны быть простыми и серийно выпускаться промышленностью.

Указанным требованиям удовлетворяют 3 элемента:

–полупроводниковый диод, в.а.х. которого близка к в.а.х. идеального диода;

–линейный резистивный элемент;

–регулируемый источник напряжения или тока.

Установим, какие простейшие характеристики можно получать с помощью элементарных блоков, составленных из перечисленных элементов.

Последовательное соединение (рис.1.2а)

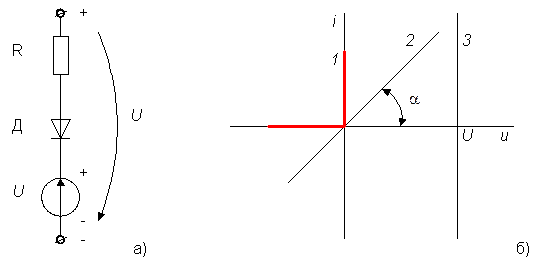
Рисунок 1.2

На рис.1.2б показаны в совмещённых координатах характеристики идеального диода –(1), линейного резистора –(2), и источника напряжения –(3). При последовательном соединении через все элементы протекает один и тот же ток и напряжения элементов складываются. Для получения в.а.х. всей цепи следует просуммировать абсциссы графиков 1, 2 и 3. Результирующая в.а.х. показана на рис.1.3 ломаной 1-3.

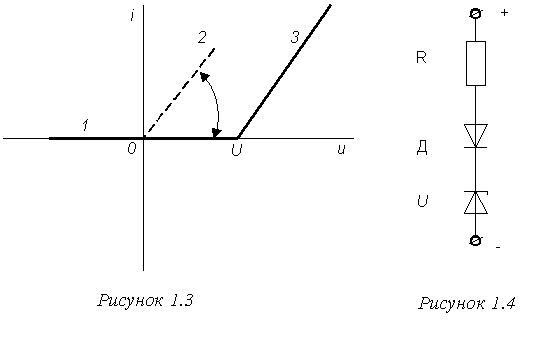
Ломаная линия 1-2 получена суммированием абсцисс графиков 1 и 2 на рис.1.2 – в.а.х. идеального диода и резистора. Отрицательная ветвь в.а.х. резистора R срезается диодом, который не пропускает обратного тока. Искомая характеристика 1-3 получается добавлением к ломаной 1-2 напряжения источника U. Точка излома определяется напряжением источника и может перемещаться по оси “u” регулированием напряжения U. Угол наклонного участка определяется значением резистора R (tga =1/R) и легко регулируется изменением сопротивления резистора.

Источник постоянного напряжения U в рассматриваемом блоке (если его применение не желательно) может быть заменен элементом, в.а.х. которого имеет вертикальный участок (например стабилитрон, включённый в обратном направлении). Схема блока со стабилитроном приведена на рис.1.4

Параллельное соединение (рис.1.5)

Рисунок 1.5

При параллельном соединении напряжения на всех элементах одинаковы, а общий ток равен сумме токов всех элементов. Просуммировав ординаты трёх в.а.х. (диода – 1, резистора – 2, источника тока – 3), получим график искомой характеристики блока в виде ломаной линии (рис.1.6).

Рисунок 1.6

Точка излома определяется током источника I и может регулироваться (перемещаться вдоль оси “i”) изменением значения тока I. Наклон участка 3 этой характеристики определяется значением сопротивления R или проводимости G=1/R.

При синтезе цепи с заданной в.а.х. поступают следующим образом:

а) заданная характеристика подвергается кусочно-линейной аппроксимации, т.е. заменяется отрезками ломаной линии;

б) кусочно-линейное приближение раскладывается на сумму элементарных характеристик, состоящих из 2-х линейных участков, которые могут быть реализованы рассмотренными выше блоками;

в) соединяя блоки последовательно или параллельно в зависимости от применённого разложения, получаем искомую цепь.

В качестве примера рассмотрим синтез цепи, моделирующей кусочно-линейную в.а.х. с 4-мя участками, приведенную на рис.1.7.

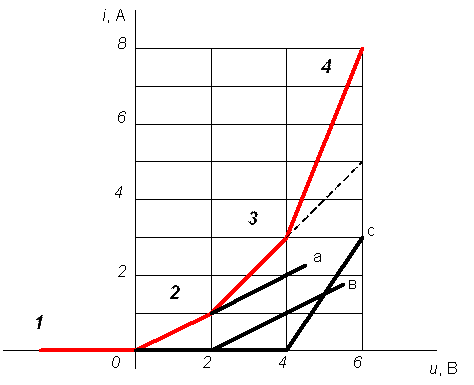
Рисунок 1.7

Угловые коэффициенты 2-го, 3-го и 4-го участков ломаной соответственно равны:

k₂=tga₂=1/2=0,5; k₃=tga₃=(3-1)/(4-2)=1; k₄=tga₄=(8-3)/(6-4)=2,5.

Разложение произведём, продолжив отрезки 2-го, 3-го и 4-го участков и отнимая их ординаты от ординат кусочно-линейной характеристики. В результате получим три составляющие элементарные характеристики а, в, с, точки излома которых лежат на оси “u”, и совпадают с абсциссами точек излома исходной характеристики. Угловые коэффициенты наклонных участков этих элементарных характеристик соответственно равны:

k_а=1/2=0,5; k_в=1/(4-2)=0,5; k_с=3/(6-4)=1,5.

Угловые коэффициенты численно равны проводимостям резистивных элементов последовательных блоков, а точки изломов – напряжениям источников.

Поскольку результирующая в.а.х. получается суммированием ординат характеристик трёх блоков, последние должны быть соединены параллельно – рис.1.8.

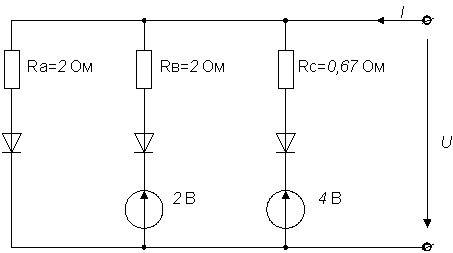
Рисунок 1.8

Рассмотренная выше методика синтеза схем с заданными в.а.х. позволяет сравнительно просто получать кусочно-линейные схемы замещения нелинейных элементов электронных цепей.