Кинематика точки. Декартовы координаты.
С неподвижной системой отсчёта связываем декартовую ортогональную систему координат (правую, рис. 31).
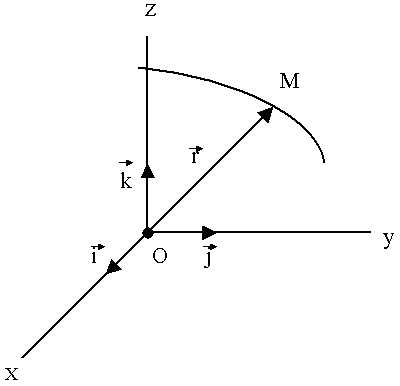
Рис.31.
Точка  , где
, где
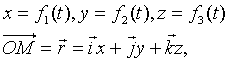 – параметрические уравнения траектории.
– параметрические уравнения траектории.
где  - единичные векторы (орты),
- единичные векторы (орты),
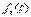 - непрерывны и 2 раза дифференцируемы; 2-е производные – непрерывны.
- непрерывны и 2 раза дифференцируемы; 2-е производные – непрерывны.
Непрерывная последовательность точек среды (пространства), занимаемая точкой M, называется траекторией точки М.
Исключая время:
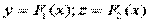
или:
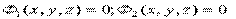
Введём понятия скорости и ускорения:
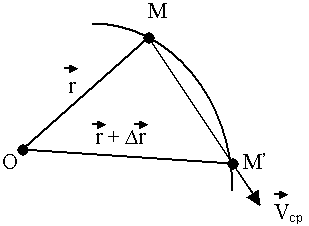
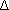 Рис.32.
Рис.32.
т. М  t
t
т. М’  t +
t + 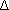 t
t
( 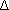 t - конечное).
t - конечное).
Радиусы – векторы: t 
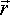
t + 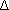 t
t 
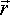 +
+ 
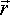
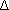
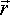 =
= 
За время 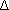 t (рис. 32):
t (рис. 32):
 (Направление по секущей MM’).
(Направление по секущей MM’).
Скорость точки в момент времени t получается при 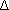 t
t  0, то есть
0, то есть
 (Направление по касательной и траектории точки)
(Направление по касательной и траектории точки)
Очевидно:
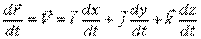
Проекции  :
:
 .
.
Модуль (длина):
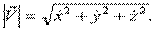
Скорость точки М в момент времени t равна производной по времени от радиуса – вектора точки и направлена по касательной к траектории.
Аналогично найдём ускорение (рис. 33).
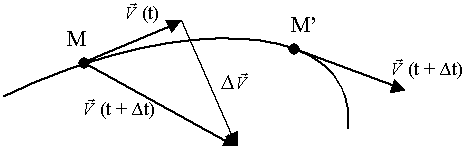
Рис.33.
Совмещая начало векторов 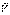 (t) и
(t) и 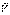 (t +
(t + 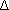 t) в точке М =>
t) в точке М => 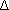
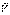 за
за 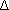 t.
t.
Среднее ускорение:
 (направление в сторону вогнутости траектории)
(направление в сторону вогнутости траектории)
Ускорение точки в момент времени t получается при 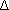 t
t  0, то есть
0, то есть
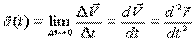
Очевидно:
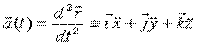

Ускорение точки в некоторый момент времени равно производной по времени от вектора скорости, или второй производной по времени от радиуса – вектора точки в этот момент времени.
В некоторых задачах – используется производная более высоких порядков, но здесь они пока не нужны.
В механике применяются не только декартовы координаты – часто применяют обобщённые (криволинейные) координаты.
Они бывают удобней, позволяют определить конфигурацию рассматриваемой системы. Часто их называют позиционными. Криволинейными они называются потому, что линии вдоль которых меняется только одна координата, обычно бывают кривыми.
Рассмотрим частный случай криволинейных координат – полярные координаты точки на плоскости: применим далее к задаче движение точек в центральном силовом поле (рис. 34).
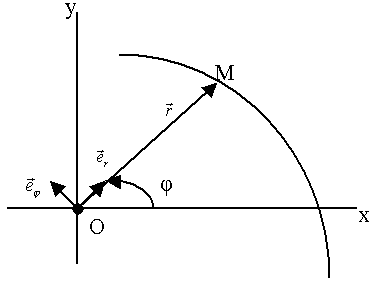
Рис.34.
(x, y) – декартовы координаты.
(r,  ) – полярные координаты.
) – полярные координаты.
Угол  => от Ох против часовой стрелки – положительное направление
=> от Ох против часовой стрелки – положительное направление
Формулы преобразования:
x = r cos  , y = r sin
, y = r sin  , где r
, где r  0; 0
0; 0 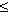
 < 2
< 2 
(можно рассматривать и 

 ).
).
Если r = const – концентрические окружности с центром в точке О.
Если  = const – прямолинейные лучи из точки О.
= const – прямолинейные лучи из точки О.
Введём два орта:

Найдём производные  по углу
по углу  (рис. 35):
(рис. 35):

Рис.35.
 (так как r = 1)
(так как r = 1)
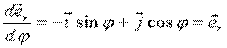 при
при 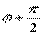 ,
,
т. е. 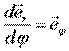 .
.
Далее:
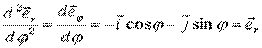 при
при 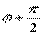 ,
,
т. е. 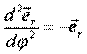 .
.
При каждом дифференцировании по φ т. е. происходит поворот на угол 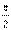 .
.
Выведем формулы проекции скорости и ускорения точки М на направления касательных к координатным линиям в полярных координатах.
Так как 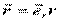 , то
, то
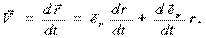
Но: 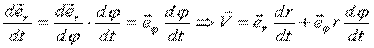
Очевидно:

Для ускорения:
 .
.
Но:  .
.
Очевидно:

Контрольные вопросы:
1. Что изучает кинематика?
2. Дайте определение скорости точки.
3. Напишите формулы проекций ускорения на оси полярной системы координат.
Лекция 9.Естественные координаты
Рассмотрим систему координатных осей, определяемую траекторией точки (рис.36).

Рис.36.
 .
.
Единичный вектор касательной к траектории (S – длина дуги М0М):
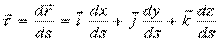 , где
, где 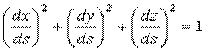 .
.
Дифференцируя 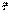 по S:
по S: 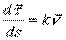 ,
,
где 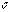 - единичный вектор главной нормали;
- единичный вектор главной нормали;  и направлен в сторону вогнутости;
и направлен в сторону вогнутости;
 кривизна. (k = 0 - прямая);
кривизна. (k = 0 - прямая); 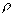 - радиус кривизны.
- радиус кривизны.
Единичный вектор бинормали 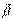 :
:
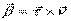 .
.
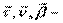 образуют правую тройку ортогональных единичных векторов. Они определяют направление естественных (натуральных) осей в том месте траектории, где находится движущаяся точка.
образуют правую тройку ортогональных единичных векторов. Они определяют направление естественных (натуральных) осей в том месте траектории, где находится движущаяся точка.
 соприкасающаяся
соприкасающаяся 
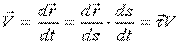
Очевидно, проекция на ось 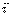 :
: 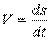 (может иметь разные знаки – зависит от направления S).
(может иметь разные знаки – зависит от направления S).
Для ускорения:
 ;
;
Но:  ;
;
Очевидно, проекции ускорения на естественные оси:
на касательную: 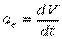 ;
;
на главную нормаль: 
на бинормаль: 0
Таким образом, ускорение лежит в соприкасающейся плоскости (рис. 37).

Рис.37.
Задача.


Контрольные вопросы:
1. Какие основные отличия естественной системы координат от декартовой?
2. Назовите проекции скорости точки в естественных координатах.
3. Какова последовательность определения радиуса кривизны траектории точки?
Лекция 10.Формула Эйлера
Найдём число координат, определяющих положение абсолютно твёрдого тела.
Определить положение тела => определить координаты 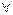 точки относительно некоторой системы отсчёта в
точки относительно некоторой системы отсчёта в  момент времени.
момент времени.
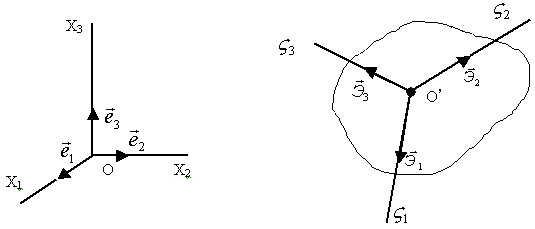
Рис.38.
Пусть Х1 , Х2 , Х3 – неподвижные оси (рис. 38); орты: 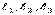 [декартова система].
[декартова система].
 ,
, 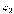 ,
,  - оси, жёстко связанные с телом; орты:
- оси, жёстко связанные с телом; орты: 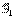 ,
,  ,
,  - [декартова система].
- [декартова система].
Так как координаты точек относительно собственных осей  ,
, 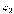 ,
,  не зависят от времени, то задача сводится к определению положения координатных осей, жёстко связанных с телом (подвижных), относительно неподвижных осей Х1 , Х2 , Х3.
не зависят от времени, то задача сводится к определению положения координатных осей, жёстко связанных с телом (подвижных), относительно неподвижных осей Х1 , Х2 , Х3.
Составим таблицу косинусов углов между осями Х и 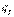 :
:
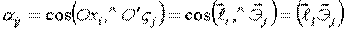
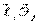 - скалярное произведение.
- скалярное произведение.

Так как системы координат ортогональны, то
скалярное произведение: 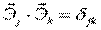 , где
, где 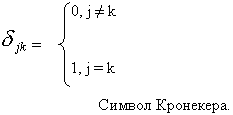
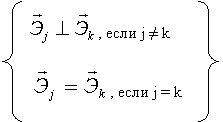

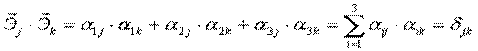
Итак: 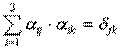
Число таких соотношений = 6 (Из 9 – ти в силу симметрии по jи k).
 Имеем 6 соотношений для 9 косинусов =>
Имеем 6 соотношений для 9 косинусов =>
3 косинуса 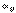 , не расположенные в одном столбце, или в одной строке, могут быть приняты за независимые, а остальные можем определить из составленных 6 – ти соотношений.
, не расположенные в одном столбце, или в одной строке, могут быть приняты за независимые, а остальные можем определить из составленных 6 – ти соотношений.
Кроме того => три координаты определяют положение точки О’ – начало системы  ,
, 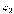 ,
,  .
.
Но 9 координат и 3 соотношения длин:

Это условия постоянства расстояний между точками в абсолютно твёрдом теле.
Выведем формулу Эйлера для распределения скоростей точек абсолютно твёрдого тела (рис. 39).

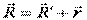 ,
,
1)  ,
,
 - скорость точки О’,
- скорость точки О’,
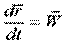 - скорость точки Q во вращательном движении тела (так как длина
- скорость точки Q во вращательном движении тела (так как длина 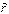 постоянна).
постоянна).
Так как координаты  точки Qпостоянны, то
точки Qпостоянны, то

Тогда:
2) 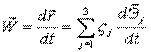 ,
,
где 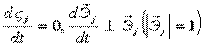 .
.
Скорость точки Q: 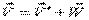 .
.
3) Выразим 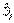 и производные через направляющие косинусы
и производные через направляющие косинусы 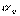 :
:
 .
.
Тогда:  (в неподвижной системе).
(в неподвижной системе).
4) Проекция  на ось
на ось  (k= 1,2,3):
(k= 1,2,3):
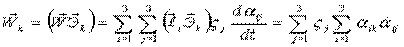 .
.
Скорости точек во вращательном движении – линейные функции координат точек.
5) Получим более простую и наглядную форму закона распределения скоростей, используя свойства функции  .
.

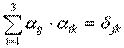 ,
,
Дифференцируем по t:
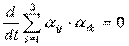 .
.
По свойству производной от произведения:
при j= k => 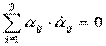 ,
,
при j≠ k=>  .
.
Свойства:
а) симметрия по kи j;
б) при j= k=>равенство «0»;
в) размерность t-1 , т. е. угловая скорость (угол в радианах), так как  - скорость.
- скорость.
г) различных только три => 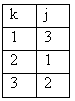
Покажем, что
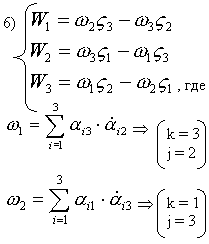

Действительно:
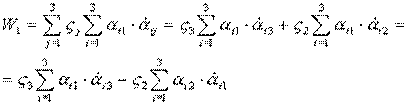

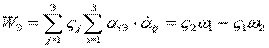 - по аналогии.
- по аналогии.
Итак:
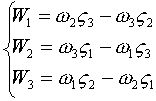
или:
7)  , где
, где 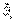 - единичные вектора, жёстко связанные с телом.
- единичные вектора, жёстко связанные с телом.
Положим  - вектор, где
- вектор, где 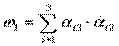
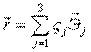


8) Тогда:

| -Описывает распределение скоростей. |
Назовём 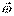 вектором мгновенной угловой скорости, а прямая на которой он располагается, в рассматриваемый момент времени, проходящую через точку О’ – осью мгновенного вращения, или мгновенной осью.
вектором мгновенной угловой скорости, а прямая на которой он располагается, в рассматриваемый момент времени, проходящую через точку О’ – осью мгновенного вращения, или мгновенной осью.
Таким образом, закон распределения скоростей точек абсолютно твёрдого тела в любом движении:
 .
.
Это формула Эйлера в векторной записи.
Контрольные вопросы:
1. Сколько координат определяют положение твёрдого тела в пространстве?
2. Что называется вектором мгновенной угловой скорости?
3. Напишите формулу Эйлера.
Лекция 11.Распределение ускорений точек твёрдого тела
Найдём закон распределения.
Дифференцируем по времени формулу Эйлера:
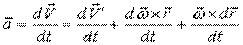 ,
,
Так как  , то
, то
 =>
=>

двойное векторное произведение 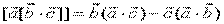
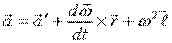 - формула Ривальса для распределения
- формула Ривальса для распределения
ускорений точек абсолютно твёрдого тела (рис. 40).
1)  - ускорение начала подвижной системы.
- ускорение начала подвижной системы.
Так как 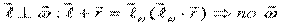
2)  - вращательное ускорение.
- вращательное ускорение.
3) 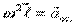 - осестремительное ускорение.
- осестремительное ускорение.

Рис.40.
Контрольные вопросы:
1. Какая формула является исходной при расчёте распределения ускорений точек твёрдого тела?
2. Как перейти от двойного векторного произведения к скалярным произведениям?
3. Напишите формулу Ривалью.
Лекция 12.Поступательное и вращательное движения
Частными видами движения абсолютно твёрдого тела являются поступательное, вращательное и плоскопараллельное.
Поступательным движением абсолютно твёрдого тела будем называть такое движение, при котором отрезок прямой, соединяющей две любые точки тела, остаётся параллельным неподвижной прямой.

Рис.41.
В поступательном движении все точки тела в каждый момент времени имеет одну и ту же скорость и одно и то же ускорение.
Пусть:

Тогда:
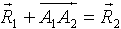
Положим:
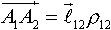 .
.
Так как 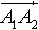 перемещается параллельно первоначальному направлению, то:
перемещается параллельно первоначальному направлению, то:
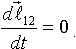
Тогда:
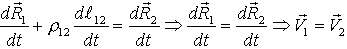
(Аналогично из формулы Эйлера при 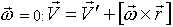 )
)
Очевидно и наоборот, если скорости всех точек равны между собой в каждый момент времени, то тело движется поступательно.
Пусть:
 ,где
,где 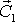 - вектор постоянной длины и неизвестного направления относительно неподвижной системы.
- вектор постоянной длины и неизвестного направления относительно неподвижной системы.
К тому же 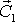 тело движется поступательно.
тело движется поступательно.
Рассмотрим вращение тела вокруг неподвижной оси.
Пусть две точки А1 и А2 неподвижны. Очевидно, что все точки прямой А1А2 неподвижны. Введём неподвижную систему Х1, Х2, Х3: Х3 по А1А2. Положение тела определяется точками А1, А2, Р, а из трех координат точки Р только одна независимая, так как имеются два уравнения связи. Можно взять угол  (рис.42).
(рис.42).

Рис.42.
Поясним: введём подвижную систему 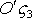 по
по 

Тогда таблица косинусов:

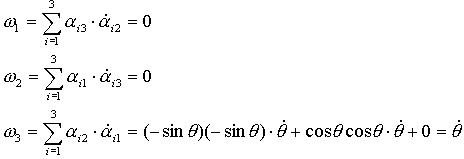
Распределение скоростей:

Распределение ускорений:

Контрольные вопросы:
1. Какое движение твёрдого тела называется поступательным?
2. Сколькими параметрами определяется положение тела при вращении вокруг неподвижной оси?
3. Напишите формулы компонент ускорения во вращательном движении тела.
Лекция 13.Плоскопараллельное движение
Плоскопараллельным называется такое движение абсолютно твёрдого тела, при котором скорости всех его точек параллельны некоторой неподвижной плоскости  .
.
 - плоскость (х1,х2)||( y1,y2).
- плоскость (х1,х2)||( y1,y2).
По формуле Эйлера:
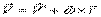
Так как  , то
, то

(круговая перестановка -  )
)
или 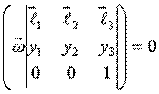 .
.
Т. е. скалярное произведение векторов  :
:
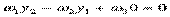 .
.
В силу произвольности координат y1, y2 точки Р =>
 .
.
Итак: вектор мгновенной угловой скорости расположен на оси  .
.
Обычно рассматривают плоское сечение тела ||  - фигуру S.
- фигуру S.
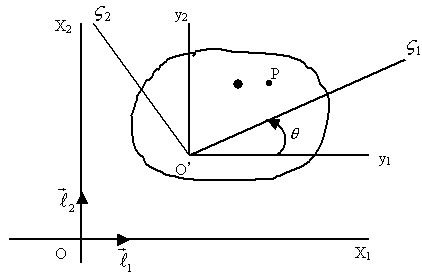
Рис.43.
Положение S определяется тремя параметрами:
1) 2 – е координаты точки О’,
2)  - угол поворота жёстко связанных осей (рис. 43).
- угол поворота жёстко связанных осей (рис. 43).
Для точки Р в плоскости (  ):
):
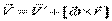 , где
, где  .
.
Или (совместив  с О):
с О):

Так как  точка в каждый момент времени, в которой скорость в этот момент равна нулю.
точка в каждый момент времени, в которой скорость в этот момент равна нулю.
Пусть это О*(х1*, х2*).
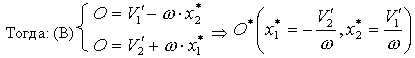
То есть если 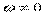 , то
, то 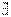 единственная точка, скорость которой равна нулю. Вычитая (В) из (А) получим:
единственная точка, скорость которой равна нулю. Вычитая (В) из (А) получим:

Если поместить начало координат в точку О*, то в этот момент времени распределение скоростей точек будет таким же, как во вращательном движении вокруг неподвижной оси. Точка О* называется центром мгновенного вращения, или мгновенным центром скоростей.
Пример: нахождение центра мгновенного вращения, если известно направление скоростей двух точек тела (рис. 44).

Рис.44.
Обратное рассуждение:
Если центр найден, то все скорости направлены  радиусу - вектору. Поэтому (обратно) для нахождения центра надо проводить
радиусу - вектору. Поэтому (обратно) для нахождения центра надо проводить  к скоростям до пересечения.
к скоростям до пересечения.
Пример: палочка АВ = l скользит по прямым Ох и Oy.
По формуле Ривальса можно найти распределение ускорений, мгновенный центр ускорений, а так же вычислить ускорение центра мгновенного вращения (и скорость мгновенного центра ускорений).
Контрольные вопросы:
1. Какое движение твёрдого тела называется плоскопараллельным?
2. Что такое мгновенный центр скоростей?
3. Как найти мгновенный центр скоростей, если известны скорости двух точек твёрдого тела?
Лекция 14.Сложное движение точки
Для описания движения введём неподвижную и подвижную системы координат.
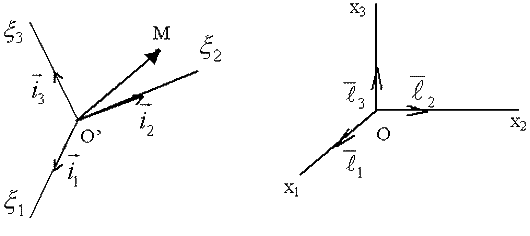
Рассмотрим движение точки М в подвижной системе отсчета  ,
, 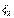 ,
,  (рис. 45). Для этого задают:
(рис. 45). Для этого задают:
1) 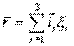 , где
, где  - орты подвижной системы.
- орты подвижной системы.
2) Движение системы 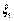 относительно неподвижных осей.
относительно неподвижных осей.
Пусть 
Найдем скорость точки М в неподвижной системе (дифференцированием):

Очевидно:
 - искомая скорость;
- искомая скорость;
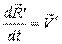 - скорость начала подвижной системы.
- скорость начала подвижной системы.
Найдём 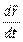 с учётом
с учётом 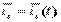 ,
, 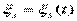


1) 
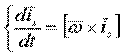 , где
, где 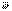 - мгновенная угловая скорость вращения подвижной системы отсчета по формуле Эйлера
- мгновенная угловая скорость вращения подвижной системы отсчета по формуле Эйлера
2) 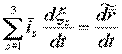 - назовем относительной производной
- назовем относительной производной
Итак:

Если 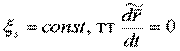 (т. е. нет относительного движения):
(т. е. нет относительного движения):
Поэтому:
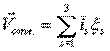 - относительная скорость.
- относительная скорость.
Переносная скорость (навязывается движением системы):

Это скорость того места, где в данный момент времени находится точка М.
Окончательно :

Найдем ускорение точки относительно неподвижной системы отсчета, если заданы относительные координаты  и движение подвижной системы.
и движение подвижной системы.
Дифференцируем:
 :
:
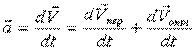

где  - ускорение точки О’
- ускорение точки О’

здесь 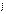 - вектор от точки М к мгновенной оси под прямым углом (см. формулу Ривальса)
- вектор от точки М к мгновенной оси под прямым углом (см. формулу Ривальса)


 - относительное ускорение (равно 0, если точка М движется в подвижной системе отсчета прямолинейно и равномерно).
- относительное ускорение (равно 0, если точка М движется в подвижной системе отсчета прямолинейно и равномерно).
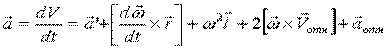
Переносное ускорение – определяется как ускорение того места в подвижной системе отсчета, в которой точка М находится в рассматриваемый момент времени; вычисляется по формуле Ривальса:

Ускорение Кориолиса: 
Половина ускорения Кориолиса получена при дифференцировании по времени переносной скорости, а вторая половина – при дифференцировании относительной скорости.
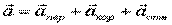 - формула Кориолиса.
- формула Кориолиса.
где 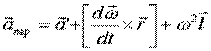 ;
;
 ;
;
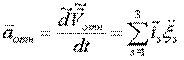
Формула Кориолиса позволяет вычислить абсолютное ускорение точки, если ее положение определяется координатами относительно подвижной системы отсчета.
Контрольные вопросы:
1. Что называется переносным и относительным движениями?
2. Напишите формулу скорости в сложном движении точки.
3. Из каких частей складывается ускорение Кориолиса?
Лекция 15.Основы динамики точки
Динамикой называется та часть, в которой рассматриваются влияние сил на состояние движения материальных объектов.
В этом разделе в качестве моделей реальных тел принимается материальная точка
Дата добавления: 2015-12-29; просмотров: 766;
