Решение задач оптимального синтеза стержневых механизмов

При постановке задачи оптимального синтеза следует различать входные и выходные параметры.

Входные – это изначально заданные параметры (размеры звеньев, скорости, ускорения или их соотношения).

Выходные – это параметры, определяемые в результате решения задачи.

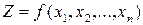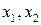При синтезе необходимо учитывать ряд требований кинематического, конструктивного, технологического характера и т. д., среди которых одно, как правило, является главным, а остальные – второстепенными (дополнительными). Если главное требование записать математически в виде функции , где - выходные параметры, то такая функция называется функцией цели (целевой), при этом дополнительные условия, выраженные в виде 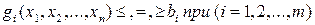, называются ограничениями.

Задачей оптимального синтеза является обеспечение экстремального значения Z при соблюдении всех ограничений.

Например, выразив вес механизма в виде функции Z его параметров (длин звеньев) можно решать задачу минимизации Z при соблюдении условий его существования. К таким условиям относятся условия проворачивания кривошипа в шарнирном четырёхзвеннике, условие соблюдения заданного угла давления и ряд других.

При малом числе выходных параметров решение задачи оптимизации может быть получено в аналитической форме. В противном случае используются численные методы направленного, случайного или комбинированного поиска оптимальных решений.

6.3. Условия проворачиваемости кривошипа в шарнирном четырёхзвеннике

При проектировании (синтезе) четырёхшарнирного механизма одним из учитываемых условий может быть проворачиваемость звеньев, то есть наличие одного или двух кривошипов. Это зависит от соотношения длин звеньев. Например, для того, чтобы звено АВ четырёхзвенника (рис. 37) могло стать кривошипом, оно должно последовательно пройти через два крайних положения. Используя три положения механизма, получим следующие условия:

для положений 1, 2, 3, предварительно обозначив длины звеньев: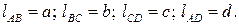

РИС. 37

При этом:

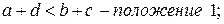
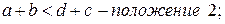
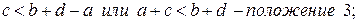
то есть сумма длин кривошипа и любого другого звена меньше суммы остальных звеньев.

Сложим попарно полученные неравенства и получим:

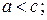
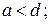
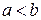, то есть кривошип является самым коротким звеном. А если данные условия не выполняются, то механизм будет либо двухкривошипным, либо двухкоромысловым. Эти условия используются при геометрическом синтезе.

6.4. Учёт углов давления в стержневых механизмах

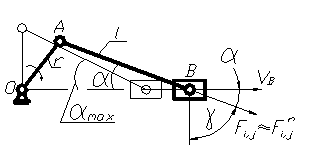Углы давления во многом определяют условия работы механизма. Так как угол давления 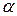(рис. 38), измеряемый между вектором силы и вектором скорости в точке её приложения, влияет на трение и износ в кинематических парах, то эти углы, в частности их максимальные значения при синтезе ограничивают для исключения возможности заклинивания и уменьшения коэффициента полезного действия.

рис. 38

Для упрощения расчётов, связанных с определением углов давления, обычно пренебрегают тангенциальными составляющими реакций, что позволяет находить наихудшие положения с точки зрения риска заклинивания и назначать длины звеньев 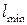, обеспечивающие приемлемые условия работы при заданном предельном угле 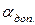(рис. 38), то есть при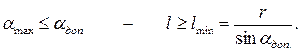

Углы 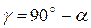называются углами передачи и ограничиваются при проектировании величиной .

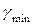6.5. Синтез четырёхзвенника по трём заданным положениям шатуна

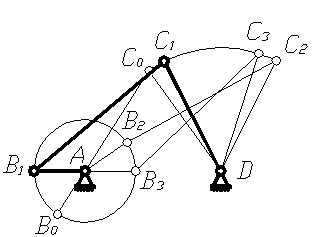
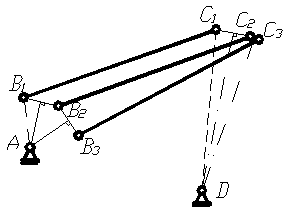Так как точки В и С шарнирного четырёхзвенника описывают дуги окружностей (рис. 39), то проведя перпендикуляры через середины хорд, соединяющих концы шатуна в трёх положениях, получим центры вращения звеньев АВ и CD (точки A и D). Вид синтеза – геометрический; способ синтеза – графический.

рис. 39