ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ И ЕГО СВОЙСТВА
Одним из основных понятий гидростатики является понятие гидростатического давления. Для его объяснения рассмотрим некоторый объем жидкости, находящийся в равновесии (рис. 2.3).
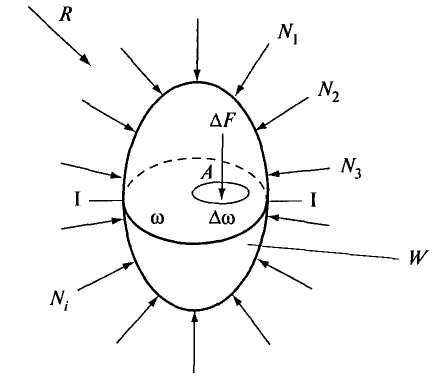
Рис. 2.3. К определению понятия гидростатического давления
Проведем секущую плоскость I-I, которая разделит объем W на две части, и отбросим мысленно одну из них, например верхнюю. Действие отброшенной части на нижнюю заменим распределенными по поверхности силами 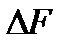 . На площадку
. На площадку 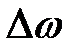 действует сила
действует сила 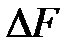 . Представим, что
. Представим, что 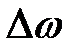 «стягивается» в т. А. Тогда предел отношения
«стягивается» в т. А. Тогда предел отношения 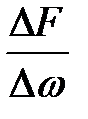 при
при 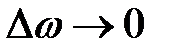 называется гидростатическим давлением в рассматриваемой точке
называется гидростатическим давлением в рассматриваемой точке
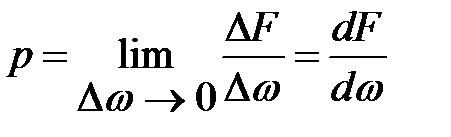 . (2.1)
. (2.1)
Следует отметить, что этот же предел отношения 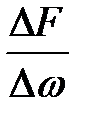 в курсе сопротивления материалов носит название упругого напряжения сжатия
в курсе сопротивления материалов носит название упругого напряжения сжатия  :
:
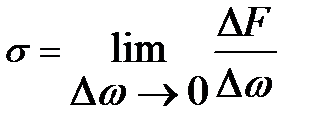 .
.
Таким образом, гидростатическое давление в рассматриваемой точке жидкости есть упругое напряжение сжатия, возникающее в жидкости под действием внешних сил. В качестве единицы измерения этой величины применяют 1 Па (один паскаль). Под 1 Па понимают давление, создаваемое силой в 1 Н, которая равномерно распределена по поверхности площадью 1 м2.
Рассмотрим свойства гидростатического давления.
Так как сила 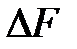 , использованная в данном определении понятия гидростатического давления, должна быть перпендикулярна площадке
, использованная в данном определении понятия гидростатического давления, должна быть перпендикулярна площадке 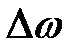 , так как жидкость находится в равновесии, то и гидростатическое давление должно быть направлено со стороны жидкости по нормали к той поверхности, на которую действует. Это и является первым свойством гидростатического давления.
, так как жидкость находится в равновесии, то и гидростатическое давление должно быть направлено со стороны жидкости по нормали к той поверхности, на которую действует. Это и является первым свойством гидростатического давления.
Выделим из покоящейся жидкости, находящейся в условиях темного тяготения, элементарный объем в виде кубика со сторонами dx, dy, dz (рис. 2.4). Оси координат направим параллельно сторонам.
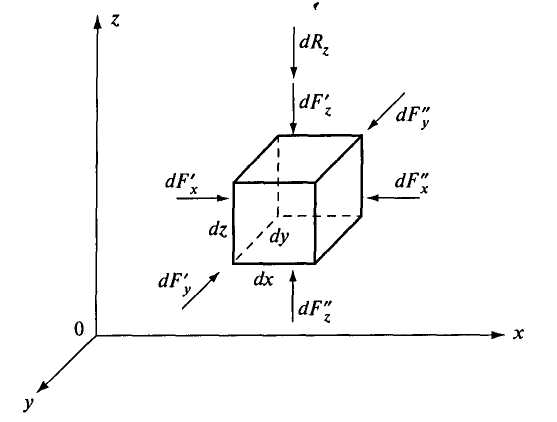
Рис. 2.4. Действие внешних сил на объем жидкости в виде элементарного кубика
Кубик находится в равновесии, значит, уравновешены поверхностные и массовые силы, действующие на кубик по всем трем осям х, у, z:
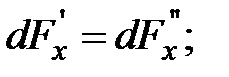
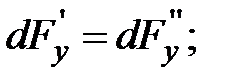
 .
.
Для условий земли единственной массовой силой R является сила тяжести, т.е. в рассматриваемом случае 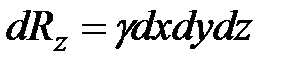 , где
, где 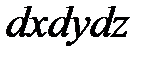 - объем кубика.
- объем кубика.
Так как 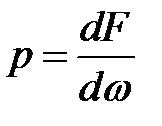 , систему уравнении можно записать в следующем виде:
, систему уравнении можно записать в следующем виде:

Сократив равенства, получим: 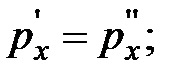
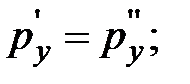
 .
.
Членом 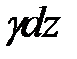 по сравнению с
по сравнению с 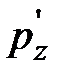 можно пренебречь как величиной бесконечно малой. Получаем, что
можно пренебречь как величиной бесконечно малой. Получаем, что 

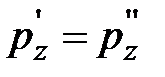 .
.
Выделенный кубик не деформируется, находясь в условиях равновесия, значит 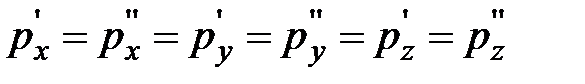 .
.
В результате логично сделать вывод: так как кубик бесконечно мал и выбран в произвольном месте, то и для любой точки жидкости гидростатическое давление одинаково по всем направлениям - это и есть второе свойство гидростатического давления.
Из этого свойства вытекает следствие: так как любая точка определяется ее координатами, гидростатическое давление в точке зависит от координат рассматриваемой точки: 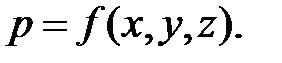
Дата добавления: 2015-12-29; просмотров: 1073;
