УДЕЛЬНАЯ ЭНЕРГИЯ СЕЧЕНИЯ, КРИТИЧЕСКАЯ ГЛУБИНА, КРИТИЧЕСКИЙ УКЛОН
Для упрощения рассмотрения неравномерного установившегося движения в русле Б. Бахметев ввел понятие удельной энергии сечения. Удельная энергия сечения 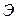 в отличие от полной удельной энергии потока
в отличие от полной удельной энергии потока 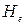 , которая определяется относительно выбранной произвольной плоскости сравнения, вычисляется, если плоскость сравнения проведена через самую нижнюю точку дна русла.
, которая определяется относительно выбранной произвольной плоскости сравнения, вычисляется, если плоскость сравнения проведена через самую нижнюю точку дна русла.
На рис. 8.4 показана схема продольного и поперечного сечений русла при неравномерном движении.
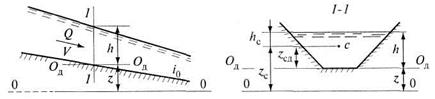
Рис. 8.4. К выводу удельной энергии сечения русла
Полная удельная энергия согласно уравнению Бернулли для выбранного живого сечения 1-1 относительно плоскости сравнения 0-0
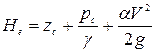 , (8.15)
, (8.15)
где 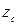 - расстояние от плоскости сравнения до центра тяжести живого сечения русла;
- расстояние от плоскости сравнения до центра тяжести живого сечения русла; 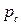 - давление в центре тяжести сечения.
- давление в центре тяжести сечения.
При расположении центра тяжести на глубине 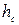 давление
давление
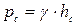 . (8.16)
. (8.16)
Полная удельная энергия
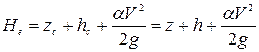 . (8.17)
. (8.17)
Для плоскости сравнения, проведенной через наинизшую точку дна русла 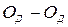 ,
, 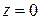 ,
, 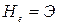 .
.
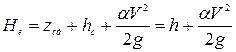 .
.
Удельная энергия сечения русла
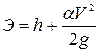 , (8.19)
, (8.19)
Или, выразив скорость 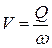 , получим
, получим
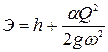
В выражении удельной энергии сечения (8.19):
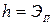 - удельная потенциальная энергия сечения;
- удельная потенциальная энергия сечения;
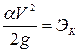 - удельная кинетическая энергия сечения.
- удельная кинетическая энергия сечения.
Тогда
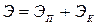 . (8.21)
. (8.21)
Проведем простейшие исследования изменений энергии сечения в зависимости от глубины жидкости в русле. Принимаем условия: расход в русле 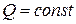 , а форма сечения русла известна и постоянна. В зависимости от глубины потока в русле изменится площадь сечения и, соответственно, средняя скорость
, а форма сечения русла известна и постоянна. В зависимости от глубины потока в русле изменится площадь сечения и, соответственно, средняя скорость 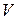 .
.
Если 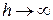 ,
, 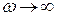 ,
, 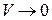 ,
, 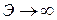 ; если
; если 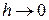 ,
, 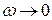 ,
, 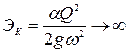 .
.
Известно, что если функция стремится к бесконечности на ее границах, то эта функция должна иметь минимум. Следовательно, функция 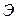 должна иметь
должна иметь 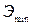 .
.
Глубина воды в русле, при которой имеет место минимум удельной энергии сечения, называется критической глубиной 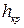 .
.
На рис. 8.5 представлен график функции удельной энергии сечения 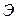 .
.
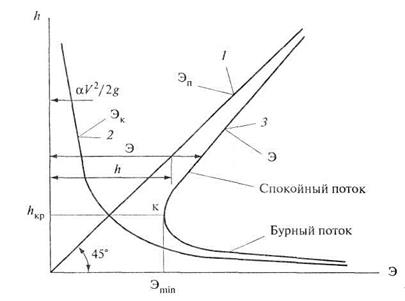
Рис. 8.5. График удельной энергии сечения
На рис. 8.5 прямая линия 1 - график изменения удельной потенциальной энергии, который имеет угол наклона 45° относительно горизонтальной координатной оси 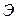 ; кривая 2 - график изменения удельной кинетической энергии имеет вид гиперболы; кривая 3 -график удельной энергии сечения
; кривая 2 - график изменения удельной кинетической энергии имеет вид гиперболы; кривая 3 -график удельной энергии сечения 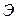 .
.
График 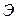 получается путем сложения значений удельных потенциальных и кинетических энергий при определенной глубине
получается путем сложения значений удельных потенциальных и кинетических энергий при определенной глубине 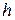 .
.
На кривой 3 имеется точка «к», которая соответствует случаю, когда функция 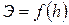 имеет минимум
имеет минимум 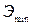 и глубину
и глубину 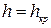 . Точка «к» делит кривую 3 на два отрезка. Верхний отрезок этой кривой соответствует условию, что глубина потока в русле
. Точка «к» делит кривую 3 на два отрезка. Верхний отрезок этой кривой соответствует условию, что глубина потока в русле 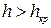 . В результате возрастания глубины кинетическая энергия уменьшается, а потенциальная - увеличивается. Потоки жидкости в руслах, в которых
. В результате возрастания глубины кинетическая энергия уменьшается, а потенциальная - увеличивается. Потоки жидкости в руслах, в которых 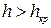 , получили название спокойных потоков.
, получили название спокойных потоков.
Нижний отрезок кривой 3 относится к потокам с глубиной 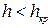 . При снижении глубины потока уменьшается площадь живого сечения, в результате этого происходит увеличение скорости и возрастание кинетической энергии, а потенциальная энергия уменьшается. Поток жидкости в русле при глубине
. При снижении глубины потока уменьшается площадь живого сечения, в результате этого происходит увеличение скорости и возрастание кинетической энергии, а потенциальная энергия уменьшается. Поток жидкости в русле при глубине 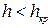 называется бурным потоком. Если глубина в русле
называется бурным потоком. Если глубина в русле 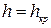 , поток жидкости находится в критическом состоянии.
, поток жидкости находится в критическом состоянии.
Значение критической глубины для русла любой формы может быть определено из условия, что функция 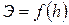 имеет минимум. Производная этой функции должна быть равна нулю,
имеет минимум. Производная этой функции должна быть равна нулю, 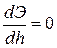 .
.
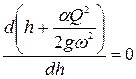 . (8.22)
. (8.22)
Тогда
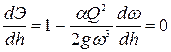 . (8.23)
. (8.23)
Площадь сечения 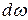 (см. рис. 8.3)
(см. рис. 8.3)
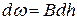 .
.
Отсюда уравнение (8.23) можно представить в виде
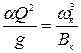 , (8.24)
, (8.24)
где 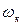 - площадь живого сечения русла при глубине
- площадь живого сечения русла при глубине 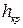 ;
;
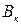 - ширина сечения русла по верху при критическом состоянии потока жидкости.
- ширина сечения русла по верху при критическом состоянии потока жидкости.
Значение критической глубины для любого русла может быть определено путем использования уравнения (8.24). Задаваясь рядом значений 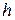 , вычисляются площадь
, вычисляются площадь 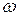 , ширина
, ширина 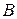 и
и 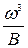 . При заданном расходе и определенном значении
. При заданном расходе и определенном значении 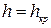 должно удовлетворяться тождество (8.24). Если построить график функции
должно удовлетворяться тождество (8.24). Если построить график функции 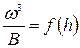 (рис. 8.6), зная значение
(рис. 8.6), зная значение 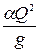 , можно по нему определить величину
, можно по нему определить величину 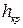 .
.
Рассмотрим русло прямоугольной формы:
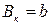 ; .
; . 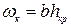 .
.
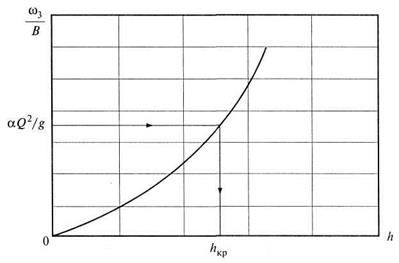
Рис. 8.6. Определение критической глубины
Выражение (8.24) для прямоугольного русла примет вид
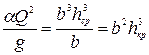 . (8.25)
. (8.25)
Отсюда критическая глубина в русле
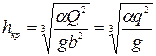 , (8.26)
, (8.26)
где 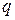 - удельный расход,
- удельный расход, 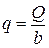 .
.
Критическая глубина зависит от формы русла и расхода жидкости. Критический уклон 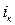 может иметь место, когда глубина жидкости в русле
может иметь место, когда глубина жидкости в русле 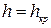 .
.
Таким образом, критическим уклоном в случае данного расхода 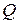 при условии равномерного движения является уклон, которому соответствует критическая глубина
при условии равномерного движения является уклон, которому соответствует критическая глубина 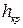 :
:
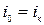 ;
; 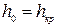 .
.
Рассмотрим равномерное движение жидкости в русле.
Расход 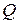 при глубине
при глубине 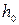 и
и 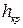 :
:
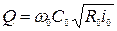 ;
;
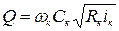 . (8.27)
. (8.27)
Следовательно, критический уклон
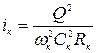 . (8.28)
. (8.28)
В зависимости от соотношения уклона дна 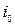 и критического уклона
и критического уклона 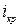 будет различным состояние движения потока:
будет различным состояние движения потока:
• 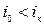 - спокойное состояние движения потока;
- спокойное состояние движения потока;
• 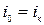 - критическое состояние движения потока;
- критическое состояние движения потока;
• 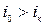 - бурное состояние движения потока.
- бурное состояние движения потока.
Для удобства определения живых сечений и глубин в открытом русле вводится параметр 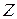 :
:
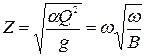 . (8.29)
. (8.29)
В случае критического состояния движения потока
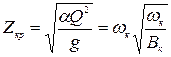 . (8.30)
. (8.30)
Критическая скорость 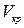 - скорость, соответствующая критическому состоянию движения потока в открытом русле с уклоном дна
- скорость, соответствующая критическому состоянию движения потока в открытом русле с уклоном дна 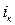 .
.
Дифференциальное уравнение в этом случае будет иметь следующий вид:
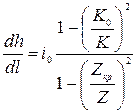 . (8.31)
. (8.31)
Пример 8.1
Определить критическую глубину 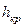 в трапецеидальном канале шириной
в трапецеидальном канале шириной 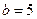 м с заложением откосов
м с заложением откосов 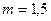 . Коэффициент шероховатости
. Коэффициент шероховатости 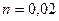 , расход воды в канале
, расход воды в канале 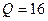 м3/с.
м3/с.
Критическую глубину находим из уравнения 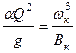 .
.
Принимая 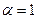 , вычисляем величину
, вычисляем величину
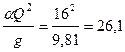 м5.
м5.
Задаемся глубинами 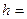 0,5; 0,7; 0,8; 0,9 и 1 м.
0,5; 0,7; 0,8; 0,9 и 1 м.
Например, 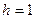 м;
м; 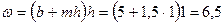 м2;
м2; 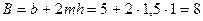 м. Вычисленные значения
м. Вычисленные значения 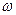 ,
, 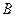 сведены в табл. 8.1.
сведены в табл. 8.1.
Таблица 8.1 - Результаты вычислений
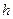 , м , м
| 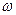 , м2 , м2
| В, м | 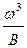 , м5 , м5
|
| 0,5 | 2,87 | 6,5 | 3,66 |
| 0,7 | 4,24 | 7,1 | 10,74 |
| 0,8 | 4,96 | 7,4 | 16,48 |
| 0,9 | 5,72 | 7,7 | 24,2 |
| 1,0 | 6,5 | 34,3 |
По данным табл. 8.1 строим график функции 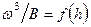 (рис. 8.7).
(рис. 8.7).
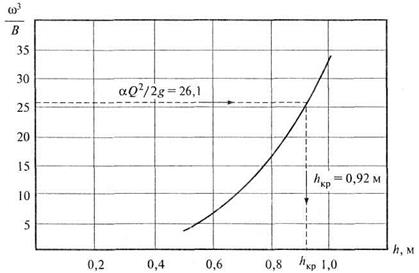
Рис. 8.7. К примеру 8.1
По графику для 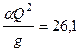 м5 находим критическую глубину
м5 находим критическую глубину 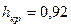 м.
м.
Дата добавления: 2015-12-29; просмотров: 1177;
