Характеристики производства
Производительность
С производственной функцией связан ряд важных характеристик производства. В первую очередь к ним относятся показатели производительности (продуктивности) ресурсов, характеризующие объем производимого продукта, приходящийся на единицу затрачиваемого ресурса каждого вида. Средним продуктом i-того ресурса называется отношение объема продукции q к объему использования этого ресурса х1:
| APi = q/xi. |
Если, например, предприятие выпускает 5 тыс. изделий в месяц, а месячные затраты труда составляют 25 тыс. часов, то средний продукт труда равен 5000/25 000 = 0.2 изд./ч.
Эта величина ничего не говорит о том, как изменится выход продукта при изменении объема затрат данного ресурса.
Если затраты i-тогo ресурса увеличились на величину , и вследствие этого выпуск продукта увеличится на величину (при неизменных затратах прочих ресурсов), то прирост выпуска на единицу прироста затрат данного ресурса определяется отношением /. Предел этого отношения при , стремящемся к нулю, получил название предельного продукта данного ресурса:
 . .
|
Если в условиях предыдущего примера число работников несколько увеличится, так что затраты труда в месяц составят 26 тыс. часов, парк оборудования, затраты сырья, энергии и тому подобное останутся прежними и при этом месячный выпуск продукции составит 5100 изделий, то предельный продукт равен приблизительно (5100-5000)/(26 000-25 000) = 0.1 изд./ч (приблизительно, так как приращения не являются бесконечно малыми).
Предельный продукт равен частной производной производственной функции по объему затрат соответствующего ресурса:
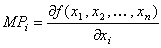 . .
|
На графике типа рис. 1, показывающем зависимость выпуска продукции от объема потребления данного ресурса при постоянных объемах прочих ресурсов ("вертикальный разрез"), величине МР соответствует угловой коэффициент наклона графика (т. е. угловой коэффициент касательной).
И средний, и предельный продукт не являются постоянными величинами, они изменяются с изменением затрат всех ресурсов. Общая закономерность, которой подчинены различные производства, получила название закона убывающего предельного продукта: с ростом объема затрат любого ресурса при постоянном уровне затрат остальных ресурсов предельный продукт данного ресурса снижается. С чем связано снижение предельного продукта? Представим себе предприятие, хорошо оснащенное различным оборудованием, имеющее достаточную площадь для осуществления производственного процесса, обеспеченное сырьем и различными материалами, но располагающее малым числом рабочих. На фоне остальных ресурсов рабочая сила является своего рода узким местом, и, надо полагать, дополнительный работник будет использован весьма рационально. Соответственно прирост продукции может быть значительным. Если же при сохранении прежних уровней всех прочих ресурсов число рабочих будет большим, труд дополнительного работника не будет уже столь хорошо обеспечен инструментом, механизмами, ему, возможно, будет мало места для работы и т. д. В этих условиях привлечение дополнительного работника не вызовет большого прироста выпуска продукции. Чем больше работников, тем меньше прирост выпуска продукции, обусловленный привлечением дополнительного работника.
Подобным же образом изменяется предельный продукт любого ресурса. Убывание предельного продукта иллюстрирует рис. 6, на котором представлен график производственной функции в предположении, что только один фактор является переменным. Зависимость объема продукта от затрат ресурса выражается вогнутой (выпуклой вверх) функцией.
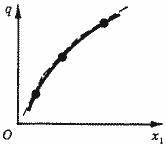
Рис. 6. Убывание предельного продукта
Некоторые авторы формулируют закон убывающего предельного продукта иначе: если объем потребления ресурса превышает некоторый уровень, то при дальнейшем увеличении потребления этого ресурса его предельный продукт снижается. При этом допускается возрастание предельного продукта при малых объемах потребления ресурса.
Кроме того, технические характеристики многих видов ресурсов таковы, что при чрезмерных объемах их использования выход продукта не увеличивается, а уменьшается, т. е. предельный продукт оказывается отрицательным. С учетом этих эффектов график производственной функции приобретает вид кривой на рис. 7, на которой выделяются три участка:
1 - предельный продукт возрастает, функция выпукла;
2 - предельный продукт убывает, функция вогнута;
3 - предельный продукт отрицателен, функция убывает.
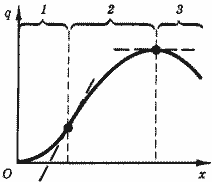
Рис. 7. Три участка производственной функции
Точки, попадающие на участок 3, соответствуют технически неэффективным вариантам производства и поэтому не представляют интереса. Соответствующая область значений затрат ресурса получила название неэкономической. К экономической области относят ту область изменения затрат ресурсов, где с ростом затрат ресурса выпуск продукта растет.
На рис. 7 это участки 1 и 2.
Но мы будем рассматривать закон убывающего предельного продукта в первой форме, т. е. будем считать предельный продукт убывающим при любых объемах затрат ресурса (в пределах экономической области).
Замещение ресурсов
Как уже отмечалось в разделе 1, одно и то же количество продукта может быть получено при различных комбинациях ресурсов, и изокванта производственной функции соединяет точки, соответствующие таким комбинациям. При переходе от одной точки изокванты к другой точке той же самой изокванты происходит уменьшение затрат одного ресурса с одновременным увеличением затрат другого, так что при этом выпуск продукции остается без изменения, т. е. имеет место замещение одного ресурса другим.
Будем считать, что производство потребляет два вида ресурсов. Меру заменяемости второго ресурса первым характеризует количество второго ресурса, компенсирующее изменение количества первого ресурса на единицу при движении по изокванте. Эта величина называется нормой технической замены и равна -Dx2/Dx1 (рис. 8). Знак "минус" связан с тем, что приращения и имеют противоположные знаки. Величина нормы замены зависит от величины приращения; чтобы избавиться от этого обстоятельства, пользуются предельной нормой технической замены:
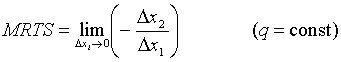 . .
|
Предельная норма технической замены связана с предельными продуктами обоих ресурсов. Обратимся к рис. 8. Переход из точки А в точку В выполним за два шага. На первом шаге увеличим количество первого ресурса; при этом выпуск продукции несколько увеличится и мы перейдем с изокванты, соответствующей выпуску q, в точку С, лежащую на изокванте . Считая приращения малыми, можем приращение представить приближенным равенством:
Dq = MP1Dx1.
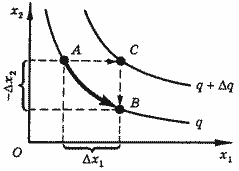
Рис. 8. Замещение ресурсов
На втором шаге уменьшим количество второго ресурса и вернемся на исходную изокванту. Отрицательное приращение выпуска при этом равно:
-Dq = MP2Dx2.
Сопоставление двух последних равенств приводит к соотношению:
-(Dx2 / Dx1) = MP1 / MP2.
В пределе, когда оба приращения стремятся к нулю, получим:
| MRTS = MP1 / MP2. (5) |
Графически предельная норма технической замены изображается взятым с обратным знаком угловым коэффициентом наклона касательной в данной точке изокванты к оси абсцисс.
При движении вдоль изокванты слева направо угол наклона касательной уменьшается - это следствие выпуклости области, расположенной над изоквантой. Предельная норма технической замены ведет себя так же, как и норма замены в потреблении. Мы рассмотрели случай, когда предприятие потребляло всего два вида ресурсов. Полученные результаты без труда переносятся на общий, n-мерный случай. Допустим, нас интересует замещение j-тогo ресурса i-тым. Мы должны зафиксировать уровни всех остальных ресурсов и рассматривать как переменные только выбранную пару. Интересующему нас замещению соответствует движение вдоль "плоской изокванты" с координатами хi, хj. Все приведенные выше соображения остаются в силе, и мы приходим к результату:
| MRTSij = MPi / MPj. (6) |
Оптимальная комбинация ресурсов
Возможность получить определенный выход продукта разными способами, или, иначе, взаимная за-мещаемость ресурсов, делает закономерным вопрос: какая комбинация ресурсов в наибольшей степени отвечает интересам предприятия?
Предприятие покупает ресурсы на рынках сырья, рабочей силы, энергии и т. д. Будем считать, что цена pi, по которой покупается i-тый ресурс, не зависит от объема покупки.
Расходы фирмы на приобретение ресурсов в двумерном случае описываются выражением:
| C = p1x1 + p2x2. |
Множество комбинаций ресурсов, расходы на покупку которых одинаковы, графически изображается, прямой - аналогом бюджетной линии в теории потребления. В теории производства эта линия называется изокостой (от англ. cost - затраты). Ее наклон определяется соотношением цен p1/p2. Постулат о рациональности поведения, лежащий в основе теоретической экономики, относится ко всем субъектам хозяйствования. Фирма, выступая на рынках ресурсов как рациональный потребитель и несущая затраты С, заинтересована в приобретении наиболее полезной комбинации ресурсов, т. е. комбинации ресурсов, дающей наибольший выход продукта. Задача определения наилучшей в этом смысле комбинации ресурсов полностью аналогична задаче нахождения потребительского оптимума. А в точке оптимума, как мы знаем, бюджетная линия касается кривой безразличия; соответственно и в точке, изображающей оптимальную комбинацию ресурсов, изокоста должна касаться изокванты (рис. 9,а). В этой точке MRTS (наклон изокванты) и отношение цен р1/р2 (наклон изокосты) совпадают. Итак, для оптимальной комбинации ресурсов выполняется равенство:
| MRTS = p1/p2. |
или, если принять во внимание равенство (5) для предельной нормы технической замены,
| MP1/MP2.= p1/p2. (7) |
Значения предельных продуктов каждого из ресурсов при оптимальной их комбинации должны быть пропорциональны их ценам.
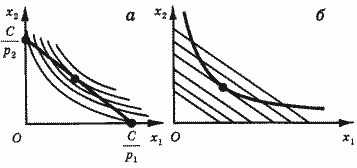
Рис. 9. Оптимальная комбинация ресурсов
Допустим, что при сложившихся объемах потребления ресурсов MP1 =0.1, MP2=0.2, а цены p1=100, p2=300. При этом MP1/MP2 = 1/2, p1/p2 = l/3, так что данная комбинация не оптимальна. Увеличивая потребление первого ресурса (при этом MP1 снизится) и уменьшая потребление второго (МР2 увеличится), можно прийти к выполнению условия (7). Значит, потребление первого ресурса было недостаточным, второго - избыточным.
Мы могли бы по-иному определить наилучшую комбинацию ресурсов. Фирма, производящая продукт в количестве q, заинтересована в выборе такого варианта производства, который позволил бы получить данный выход продукта при наименьших расходах на приобретение ресурсов. Задача сводится к отысканию на заданной изокванте такой точки, которая располагалась бы на самой низкой изокосте. И в этом случае искомая комбинация изображается точкой касания изокванты и изокосты (рис. 9,б), а для нее должно выполняться соотношение (7). В отличие от потребителя, доход которого предполагается заданным, для фирмы ни расходы на ресурсы, ни выпуск продукции не являются заданными величинами. И то и другое - результат согласованного выбора с учетом ситуации на рынке продукта. Однако, зная цены ресурсов, мы можем выделить экономически эффективные варианты производственного процесса. Будем называть вариант экономически эффективным, если фирма не может увеличить выпуск продукта без увеличения расходов на ресурсы и не может снизить расходов без сокращения выпуска. На рис. 10. точка Е соответствует эффективному, а точки А и В - неэффективным вариантам: вариант А дороже, чем Е, при том же выходе продукта; варианту В соответствуют те же затраты, что и варианту Е, но выход продукта здесь меньше. Пропорциональность предельных продуктов ценам ресурсов мы можем теперь трактовать как условие экономической эффективности производственного варианта.
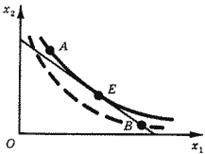
Рис. 10. Экономически эффективный и экономически неэффективный варианты производства
Этот вывод также легко переносится на n -мерный случай. Если комбинация ресурсов (х1, х2, ..., хn) экономически эффективна, то любая пара (xi, xj) peсурсов должна удовлетворять условию вида (7), т. е. равенство:
| MPi / MPj = pi/pj |
должно выполняться для любой пары ресурсов. А это возможно, если предельные продукты всех ресурсов пропорциональны ценам:
| MP1 : MP2 : ┼ : MPn = p1 : p2 : ┼: pn. (8) |
Считая цены ресурсов фиксированными, возьмем на каждой изокванте самую "дешевую" точку (или на каждой изокосте - самую "производительную") и соединим их кривой. Эта кривая объединяет варианты, эффективные при данных ценах ресурсов. Принимая решение об объеме производства, фирма будет оставаться на этой кривой. Ее называют кривой оптимального роста (рис. 11). Приведенные утверждения справедливы в предположении, что фирма может свободно выбирать объемы всех ресурсов. Однако предприятие может в короткий срок резко изменить потребление материалов, может принять на работу требуемое количество работников, но не может столь же быстро изменить, например, производственные площади. В связи с этим различают поведение фирмы в коротком и длительном периодах: в длительном периоде могут изменяться объемы всех ресурсов, в коротком - только некоторых.
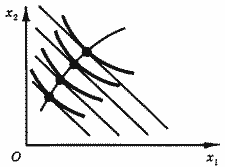
Рис. 11. Кривая роста
Пусть из двух ресурсов, потребляемых предприятием, первый может изменяться в коротком периоде, а второй - только в длительном, в коротком же принимает фиксированное значение х2 = В. Эту ситуацию иллюстрирует рис. 12. В длительном периоде предприятие может выбрать любую комбинацию ресурсов в пределах положительного квадранта плоскости х1х2, а в коротком - лишь на луче ВС.
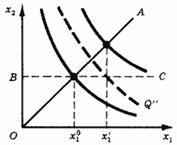
Рис. 12. Изменение масштаба в длительном к коротком периодах
В общем случае все ресурсы можно разделить на изменяющиеся в коротком периоде ("подвижные") и изменяющиеся только в длительном периоде. В коротком периоде могут рационально выбираться лишь объемы "подвижных" ресурсов, так что условие экономической эффективности - пропорция вида (8) - в коротком периоде охватывает только эти виды ресурсов. Вариант, эффективный в коротком периоде, может быть неэффективным в длительном.
Отдача от масштаба
Допустим, что фирма желает увеличить выпуск продукта вдвое. Достигнет ли она этой цели, удвоив затраты труда, парк оборудования, производственные площади, словом, объемы всех используемых ресурсов? Или этой цели можно достичь не столь большим ростом затрат ресурсов? Или, напротив, для этой цели расход ресурсов нужно увеличить больше, чем в два раза? Ответ на такие вопросы дает характеристика производства, получившая название отдачи от масштаба.
Обозначим x01, x02 объемы потребления фирмой ресурсов в исходном состоянии; количество производимого продукта при этом равно:
| q0 = f(x01, x02)ю |
Пусть теперь фирма изменяет масштаб потребления ресурсов, сохраняя пропорцию между их количествами: x`1 = kx01, x`2 = kx01.
Новый объем производства продукта равен:
| q` = f(kx01, kx02). |
Возможны случаи, когда выпуск продукта изменяется в той же самой пропорции, что и потребление ресурсов, т. е. q` = kq0.Тогда говорят о постоянной отдаче от масштаба.
Но может оказаться и иначе. Например, увеличение потребления ресурсов в 2 раза вызовет увеличение выпуска в 2.5 раза. Если q` > kq0, говорят о возрастающей отдаче от масштаба. Если же q` < kq0, то мы имеем дело с убывающей отдачей от масштаба (скажем, удвоение затрат каждого ресурса позволяет увеличить выпуск продукта лишь в 1.5 раза).
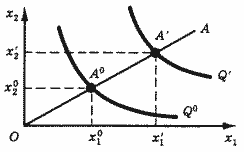
Рис. 13. Пропорциональное изменение потребления ресурсов
На карте изоквант пропорциональное изменение расхода ресурсов изображается движением вдоль луча, выходящего из начала координат (рис. 13).
Увеличение расхода в k раз соответствует увеличению в k раз расстояния от начала координат.
Изокванты, пересекающие луч ОА в различных точках, показывают, как при продвижении вдоль луча изменяется объем выпуска продукта. Выбрав в качестве единицы длины расстояние от начала координат до исходной точки А0, можно построить график изменения объема выпуска в зависимости от масштабного коэффициента k. Рис. 14 иллюстрирует постоянную (а), возрастающую (б) и убывающую (в) отдачу от масштаба.

Рис. 14. Постоянная (а), возрастающая (б) и убывающая (в) отдача от масштаба
Таким образом, если предприятие хочет увеличить выпуск продукта в k раз, сохраняя пропорцию между объемами потребления ресурсов, то ему придется увеличить объем потребления каждого ресурса:
- в k раз, если отдача от масштаба постоянна;
- меньше, чем в k раз, если отдача от масштаба возрастает;
- больше, чем в k раз, если отдача от масштаба убывает.
Если масштаб производства может изменяться в широких пределах, то характер отдачи от масштаба не остается одним и тем же во всем диапазоне изменений.
Для того чтобы фирма могла функционировать, требуется некоторый минимальный уровень потребления ресурсов - постоянные затраты.
При малых объемах производства отдача от масштаба оказывается возрастающей: так как величина постоянных затрат остается неизменной, значительное увеличение выпуска продукта может быть достигнуто при относительно небольшом увеличении общих затрат ресурсов.
При больших объемах отдача от масштаба оказывается убывающей вследствие снижения предельного продукта каждого ресурса.
Помимо других обстоятельств убывающая отдача от масштаба на крупных предприятиях связана с усложнением управления производством, нарушениями координации деятельности различных производственных звеньев и т. д. Характерная кривая представлена на рис. 15. Участок слева от точки В характеризуется возрастающей отдачей от масштаба, справа - убывающей. В окрестности точки В отдача от масштаба приблизительно постоянна.

Рис. 15. Различная отдача от масштаба на различных участках кривой
Дата добавления: 2015-12-29; просмотров: 866;
