Теория производства
РАЗДЕЛ 1. Производственная функция
Производство не может создавать продукцию из ничего. Процесс производства связан с потреблением различных ресурсов. В число ресурсов входит все то, что необходимо для производственной деятельности, - и сырье, и энергия, и труд, и оборудование, и пространство.
Для того чтобы описать поведение фирмы, необходимо знать, какое количество продукта она может произвести, используя ресурсы в тех или иных объемах. Мы будет исходить из допущения, что фирма производит однородный продукт, количество которого измеряется в натуральных единицах - тоннах, штуках, метрах и т. д. Зависимость количества продукта, которое может произвести фирма, от объемов затрат ресурсов получила название производственной функции.
Но предприятие может по-разному осуществить производственный процесс, используя разные технологические способы, разные варианты организации производства, так что и количество продукта, получаемое при одних и тех же затратах ресурсов, может быть разным. Руководители фирмы должны отклонить варианты производства, дающие меньший выход продукта, если при тех же самых затратах каждого вида ресурса можно получить больший выход. Точно так же они должны отклонить варианты, требующие больших затрат хотя бы одного ресурса без увеличения выхода продукта и сокращения затрат других ресурсов. Варианты, отклоняемые по этим соображениям, носят название технически неэффективных.
Допустим, ваша фирма производит холодильники. Для изготовления корпуса нужно раскроить листовое железо. В зависимости от того, как будет размечен и раскроен стандартный лист железа, из него можно вырезать больше или меньше деталей; соответственно-для изготовления определенного количества холодильников потребуется меньше или больше стандартных листов железа.
При этом расход всех остальных материалов, труда, оборудования, электроэнергии останется без изменения. Такой вариант производства, который может быть улучшен путем более рационального раскроя железа, должен быть признан технически неэффективным и отклонен.
Технически эффективными называют варианты производства, которые нельзя улучшить ни увеличением производства продукта без увеличения расхода ресурсов, ни сокращением затрат какого-либо ресурса без снижения выпуска и без увеличения затрат других ресурсов.
Производственная функция учитывает только технически эффективные варианты. Ее значение - это наибольшее количество продукта, которое может произвести предприятие при данных объемах потребления ресурсов.
Рассмотрим вначале простейший случай: предприятие производит единственный вид продукции и расходует единственный вид ресурса.
Пример такого производства довольно трудно найти в действительности. Даже если рассмотреть предприятие, оказывающее услуги на дому у клиентов без применения какого-либо оборудования и материалов (массаж, репетиторство) и затрачивающее только труд работников, нам пришлось бы допустить, что работники обходят клиентов пешком (не используя услуг транспорта) и договариваются с клиентами без помощи почты и телефона. Итак, предприятие, затрачивая ресурс в количестве х, может произвести продукт в количестве q.
Производственная функция:
| q = f(x) (1) |
устанавливает связь между этими величинами. Заметим, что здесь, как и в других лекциях, все объемные величины - это величины типа потока: объем затрат ресурса измеряется количеством единиц ресурса в единицу времени, а объем выпуска - количеством единиц продукта в единицу времени.
На рис. 1 приведен график производственной функции для рассматриваемого случая. Все точки, лежащие на графике, соответствуют технически эффективным вариантам, в частности точки А и В. Точка С соответствует неэффективному, а точка D - недостижимому варианту.
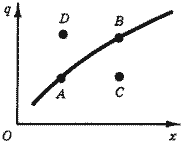
Рис. 1. Производственная функция в случае единственного ресурса
Производственная функция вида (1), устанавливающая зависимость объема производства от объема затрат единственного ресурса, может использоваться не только в иллюстративных целях. Она полезна и тогда, когда может изменяться расход лишь одного ресурса, а затраты всех остальных ресурсов по тем или иным причинам должны рассматриваться как фиксированные. В этих случаях интерес представляет зависимость объема производства от затрат единственного переменного фактора.
Значительно большее разнообразие появляется при рассмотрении производственной функции, зависящей от объемов двух потребляемых ресурсов:
| q = f(x1, x2) (2) |
Анализ таких функций позволяет легко перейти к общему случаю, когда количество ресурсов может быть любым. Кроме того, производственные функции двух аргументов широко используются в практике, когда исследователя интересует зависимость объема выпуска продукта от важнейших факторов - затрат труда (L) и капитала (K):
| q = f(L, K). (3) |
График функции двух переменных невозможно изобразить на плоскости.
Производственную функцию вида (2) можно представить в трехмерном декартовом пространстве, две координаты которого (x1 и x2) откладываются на горизонтальных осях и соответствуют затратам ресурсов, а третья (q) откладывается на вертикальной оси и соответствует выпуску продукта (рис. 2). Графиком производственной функции служит поверхность "холма", повышающаяся с ростом каждой из координат x1 и x2. Построение на рис. 1 при этом можно рассматривать как вертикальный разрез "холма" плоскостью, параллельной оси x1 и соответствующей фиксированному значению второй координаты x2 = x*2.
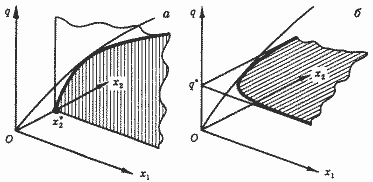
Рис. 2. Производственная функция в случае двух ресурсов
Горизонтальный разрез "холма" объединяет варианты производства, характеризующиеся фиксированным выпуском продукта q = q* при различных сочетаниях затрат первого и второго ресурсов. Если горизонтальное сечение поверхности "холма" изобразить отдельно на плоскости с координатами x1 и x2, получится кривая, объединяющая такие комбинации затрат ресурсов, которые позволяют получить данный фиксированный объем выпуска продукта (рис. 3). Такая кривая получила название изокванты производственной функции (от греч. isoz - одинаковый и лат. quantum - сколько).
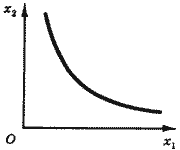
Рис. 3. Изокванта производственной функции
Допустим, что производственная функция описывает выпуск продукции в зависимости от затрат труда и капитала. Одно и то же количество продукции можно получить при различных сочетаниях затрат этих ресурсов. Можно использовать небольшое количество машин (т. е. обойтись небольшими затратами капитала), но при этом придется затратить большое количество труда; можно, напротив, механизировать те или иные операции, увеличить количество машин и за счет этого снизить затраты труда. Если при всех таких сочетаниях наибольший возможный объем выпуска остается постоянным, то эти сочетания изображаются точками, лежащими на одной и той же изокванте.
Зафиксировав объем выпуска продукта на другом уровне, мы получим другую изокванту той же самой производственной функции. Выполнив серию горизонтальных разрезов на различных высотах, получим так называемую карту изоквант (рис. 4) - наиболее распространенное графическое представление производственной функции от двух аргументов. Она похожа на географическую карту, на которой рельеф местности изображен горизонталями (иначе - изо-гипсами) - линиями, соединяющими точки, лежащие на одинаковой высоте.
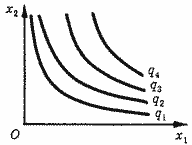
Рис. 4. Карта изоквант
Нетрудно заметить, что производственная функция во многом похожа на функцию полезности в теории потребления, изокванта - на кривую безразличия, карта изоквант - на карту безразличия. Позже мы убедимся в том, что свойства и характеристики производственной функции имеют много аналогий в теории потребления. И дело тут не в простом сходстве. По отношению к ресурсам фирма ведет себя как потребитель, и производственная функция характеризует именно эту сторону производства - производство как потребление. Тот или иной набор ресурсов полезен для производства постольку, поскольку он позволяет получить соответствующий объем выпуска продукта. Можно сказать, что значения производственной функции выражают полезность для производства соответствующего набора ресурсов. В отличие от потребительской полезности эта "полезность" имеет вполне определенную количественную меру - она определяется объемом производимой продукции.
То обстоятельство, что значения производственной функции относятся к технически эффективным вариантам и характеризуют наибольший выпуск продукции при потреблении данного набора ресурсов, также имеет аналогию в теории потребления.
Потребитель может по-разному использовать приобретаемые блага. Полезность покупаемого набора благ определяется таким способом их использования, при котором потребитель получает наибольшее удовлетворение.
Однако при всех отмеченных чертах сходства потребительской полезности и "полезности", выражаемой значениями производственной функции, это совершенно разные понятия. Потребитель сам, исходя только из своих собственных предпочтений, определяет, насколько полезен для него тот или иной продукт, - покупая или отвергая его.
Набор производственных ресурсов в конечном счете окажется полезным в той мере, в какой будет одобрен потребителем тот продукт, который произведен с использованием этих ресурсов.
Поскольку производственной функции присущи наиболее общие свойства функции полезности, мы можем далее рассмотреть основные ее свойства, не повторяя подробных рассуждений, приведенных во II части.
Будем считать, что увеличение затрат одного из ресурсов при неизменных затратах другого позволяет увеличить выход продукции. Это значит, что производственная функция - возрастающая функция каждого из своих аргументов. Через каждую точку плоскости ресурсов с координатами х1, х2 проходит единственная изокванта. Все изокванты имеют отрицательный наклон. Изокванта, отвечающая большему выходу продукта, располагается правее и выше изокванты для меньшего выхода. Наконец, все изокванты будем считать выпуклыми в направлении начала координат.
На рис. 5 изображены некоторые карты изоквант, характеризующие различные ситуации, возникающие при производственном потреблении двух ресурсов. Рис. 5,а соответствует абсолютному взаимозамещению ресурсов. В случае, представленном на рис. 5,б, первый ресурс может быть полностью замещен вторым: точки изоквант, расположенные на оси х2 показывают количество второго ресурса, позволяющее получить тот или иной выход продукта без использования первого ресурса. Использование первого ресурса позволяет сократить затраты второго, но полностью заменить второй ресурс первым невозможно.
Рис. 5,в изображает ситуацию, в которой оба ресурса необходимы и ни один из них не может быть полностью замещен другим. Наконец, случай, представленный на рис. 5,г, характеризуется абсолютной взаимодополняемостью ресурсов.
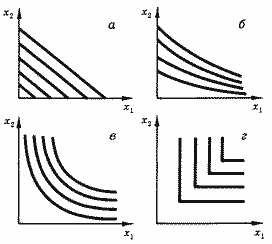
Рис. 5. Примеры карт изоквант
Производственная функция, зависящая от двух аргументов, имеет довольно наглядное представление и сравнительно проста для расчетов. Нужно заметить, что в экономике используются производственные функции различных объектов - предприятия, отрасли, национального и мирового хозяйства. Чаще всего это функции вида (3); иногда добавляют третий аргумент - затраты природных ресурсов (N):
| q = f(L, K, N). |
Это имеет смысл, если количество природных ресурсов, вовлекаемых в производственную деятельность, является переменным.
В прикладных экономических исследованиях и в экономической теории используются производственные функции разных типов. Их особенности и различия будут обсуждаться в разделе 3. В прикладных расчетах требования практической вычислимости заставляют ограничиться небольшим числом факторов, и эти факторы рассматриваются укрупненно - "труд" без подразделения по профессиям и квалификации, "капитал" без учета его конкретного состава, и т. д. При теоретическом анализе производства можно отвлечься от трудностей практической вычислимости. Теоретический подход требует каждый вид ресурса считать абсолютно однородным. Сырье различных сортов должно рассматриваться как различные виды ресурсов, точно так же, как машины различных марок или труд, различающийся по профессиональному и квалификационному признакам.
Таким образом, используемая в теории производственная функция - это функция большого числа аргументов:
| q = f(x1, x2, ..., xn). (4) |
Такой же подход применялся и в теории потребления, где число видов потребляемых благ никак не ограничивалось.
Все, что было ранее сказано о производственной функции двух аргументов, может быть перенесено и на функцию вида (4), разумеется, с оговорками, касающимися размерности.
Изокванты функции (4) - это не плоские кривые, а n-мерные поверхности. Тем не менее мы и в дальнейшем будем пользоваться "плоскими изоквантами" - и в иллюстративных целях, и как удобным средством анализа в случаях, когда затраты двух ресурсов являются переменными, а остальных считаются фиксированными.
Дата добавления: 2015-12-29; просмотров: 1065;
