Общие сведения и характеристика
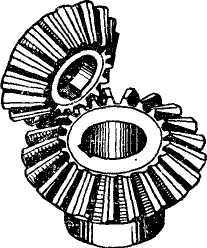
Конические зубчатые колёса применяют в передачах, у которых оси валов пересекаются под некоторым углом ∑ (рис. 4.21, 4.22). Наиболее распространены передачи с углом ∑= 900.
|
| Рис. 4.21 |
Геометрические параметры. Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются
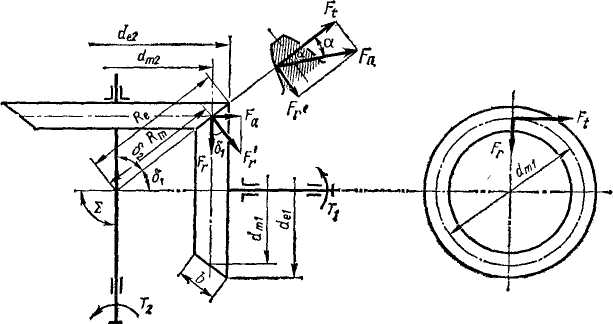 Рис. 4.22
Рис. 4.22
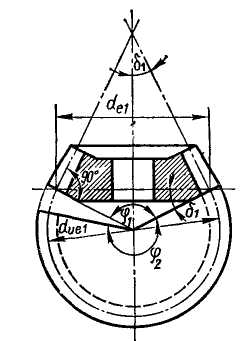
начальные и делительные конусы с углами б1 и б2. При коэффициентах смещения инструмента x1+ x2=0 начальные и делительные конусы совпадают. Этот наиболее распространенный вариант рассматривается ниже. Конусы, образующие которых перпендикулярны образующим делительных конусов (см. рис. 4.23), называют дополнительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения. Размеры, относящиеся к внешнему торцовому сечению, сопровождают индексом е. Например: de, Re и др. Размеры в среднем сечении сопровождают индексом т — dm, Rm и др.;
Re и Rm — внешнее исреднее конусное расстояние, b — ширина зубчатого венца.
Размеры по внешнему торцу удобнее для измерения, их указывают на чертежах. Размеры в среднем сечении используют при силовых расчетах. Зависимости размеров в среднем и торцовом сечениях;
Re=Rm+0,5b, de=dmReRm, mte=mtmRe/Rm. (4.28)
Для прямозубых передач торцовое t и нормальное п сечения совпадают. При этом mte=mne округляют до стандартного.
Передаточное число.Как и у цилиндрических передач : 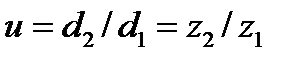
Кроме того, выразив d1 иd2 через конусное расстояние R и углы делительных конусов б1 и б2, получим 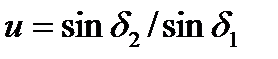 и при сумме ∑= б1 + б2 = 900
и при сумме ∑= б1 + б2 = 900 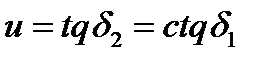 (4.29)
(4.29)
Формулы (4.29) используют для определения углов б1 и б2 .
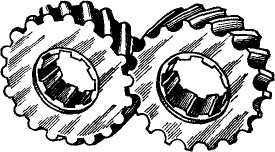
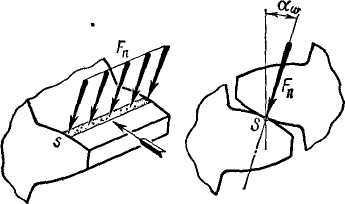
Силы в зацеплении прямозубой конической передачи.В зацеплении конической передачи действуют силы: окружная Ft, радиальная Fr и осевая F а. Зависимость между этими силами нетрудно установить с помощью рис. 4.22, где силы изображены приложенными к шестерне.
По нормали к зубу действует сила Fn, которую раскладывают на Ft и F'r. В свою очередь F'r раскладывается на Fа и FT. Здесь
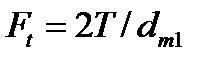
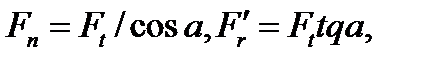
Fr = F'r cos 8,=F t tg a cos 81, (4.30)
 Fa = F'r sin б1= Ft tg a sin б1.
Fa = F'r sin б1= Ft tg a sin б1.
Для колеса направление сил противоположно. При этом Fa — радиальная сила, а Fr — осевая.
Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому.Параметры эквивалентных колес используют при расчетах на прочность. Форма зуба конического колеса в нормальном сечении дополнительным конусом см. (рис. 4.22) такая же, как у цилиндрического прямозубого колеса. Эквивалентное цилиндрическое колесо получим как развертку дополнительного конуса — ограниченного углом 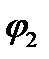 . Диаметры эквивалентных колес
. Диаметры эквивалентных колес
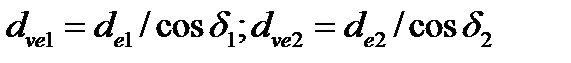 . (4.31)
. (4.31)
Выражая диаметры через zи т, запишем 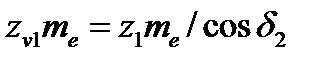 или числа зубьев эквивалентных колес
или числа зубьев эквивалентных колес 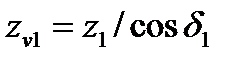 ,
, 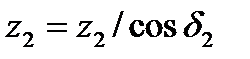 . (4.32)
. (4.32)
(Допускают применение нестандартных модулей, если это не связано с применением специального инструмента)
|
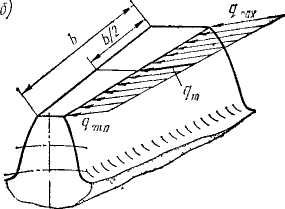
Расчет зубьев прямозубой конической передачи по напряжениям изгиба.Размеры поперечных сечений зуба конического колеса изменяются пропорционально расстоянию этих сечений от вершины конуса (рис. 8.32, а). Все поперечные сечения зуба, геометрически подобны. При этом удельная нагрузка q распределяется неравномерно по длине зуба. Она изменяется в зависимости от деформации и жесткости зуба в различных сечениях. Можно доказать, что нагрузка q распределяется по закону треугольника, вершина которого совпадаете вершиной делительного конуса, и что напряжения изгиба одинаковы по всей длине зуба.
| Рис.4.23 |
При геометрическом подобии зубьев в различных сечениях их жесткость, как консольных оболочек, постоянна по всей ширине ко леса. Для оценки деформации положим, что зубья колеса 2 абсолютно жесткие, а зубья колеса 1 податливые. При заторможенном колес 2 нагруженное колесо 1 повернется на угол ∆φ вследствие податливости зубьев. Прогиб зубьев в различных сечениях равен r*∆φ, где
r — радиус в соответствующем сечении. При постоянной жесткости нагрузка пропорциональна деформациям или в нашем случае радиусам r, которые в свою очередь пропорциональны расстояниям от вершины делительного конуса — рис. 4.24, б. Если модуль зубьев инагрузка изменяются одинаково, то напряжения изгиба остаются постоянными [см. формулу (4.19)] по всей длине зуба.
|
|
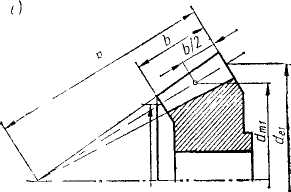
Рис.4.24
Это позволяет вести расчет по любому из сечений. На практике за расчетное сечение принято среднее сечение зуба с нагрузкой qm. По аналогии с прямозубой цилиндрической передачей [формула (4.14)]запишем
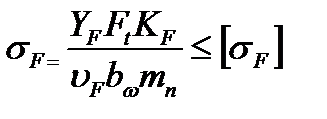 , (4.33)
, (4.33)
где для прямозубой передачи 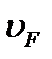 =0,85 — опытный коэффициент (см, выше); тn — модуль в среднем нормальном сечении зуба.
=0,85 — опытный коэффициент (см, выше); тn — модуль в среднем нормальном сечении зуба.
Коэффициент формы зуба YF определяют по справочной литературе в соответствии с эквивалентным числом зубьев zv. Коэффициент нагрузки КР см. ниже.
Расчет зубьев прямозубой конической передачи по контактным напряжениям. Для конического зацепления рпр в формуле (4.7) определяют по диаметрам эквивалентных колес. Согласно формулам (4.31) для среднего сечения зуба имеем
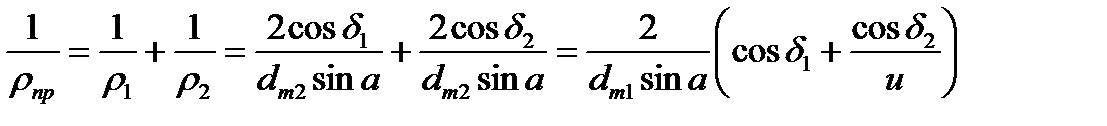 .
.
Учитывая связь тригонометрических функций и формулу (4.29), после преобразований получим: 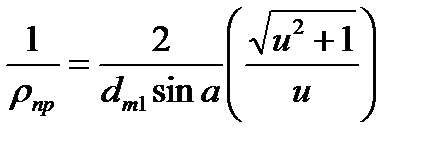 . (4.34)
. (4.34)
На основании формулы (4.34) можно отметить, что приведенный радиус кривизны в различных сечениях зуба конического колеса изменяется пропорционально диаметрам этих сечений или расстоянию от вершины начального конуса. Ранее было сказано, что удельная нагрузка q также пропорциональна этим расстояниям. Следовательно, отношение 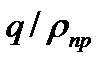 постоянно для всех сечений зуба. При этом постоянными остаются и контактные напряжения по всей длине зуба, что позволяет производить расчет по любому сечению (в данном случае по среднему). Удельная нагрузка в этом сечении (см. рис. 4.24)
постоянно для всех сечений зуба. При этом постоянными остаются и контактные напряжения по всей длине зуба, что позволяет производить расчет по любому сечению (в данном случае по среднему). Удельная нагрузка в этом сечении (см. рис. 4.24)
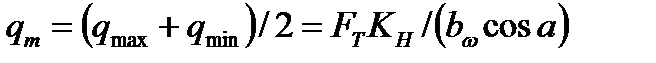 . (4.35)
. (4.35)
Сравнивая формулы (4.34) и (4.35) с аналогичными формулами (4.8) и (4.9) для прямозубых цилиндрических передач, отмечаем, что формулы для q совпадают, а для 1/рпр различаются только числителями: 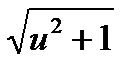 вместо (u+1). Учитывая_это различие, переписываем формулу (4.10) для проверочного расчета прямозубых конических передач в виде
вместо (u+1). Учитывая_это различие, переписываем формулу (4.10) для проверочного расчета прямозубых конических передач в виде
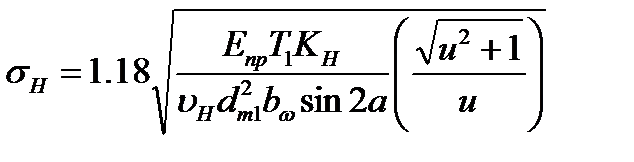 (4.36)
(4.36)
где 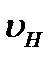 = 0,85 — опытный коэффициент (см. выше).
= 0,85 — опытный коэффициент (см. выше).
Для проектного расчета формулу (4.36) преобразуют. При этом учитывают, что основными габаритными размерами для конических передач являются de2 и Re, а нагрузка характеризуется моментом Т2 на ведомом валу. Вводим эти параметры в формулу (4.36) и после преобразований получаем 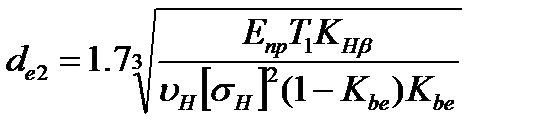 , (4.37)
, (4.37)
где Kb e= bw / Re — коэффициент ширины зубчатого венца относительно внешнего конусного расстояния. Рекомендуют Кbе<0,3. Наиболее распространено значение Кbе =0,285.
В этом случае 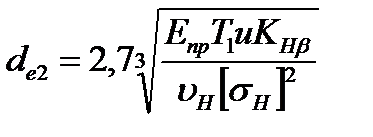 , при а = 20° и КHv =1,5 (4.38)
, при а = 20° и КHv =1,5 (4.38)
Коэффициенты расчетной нагрузкиКH и КF выбираются по справочной литературе.
4.9. Конические передачи с непрямыми зубьями
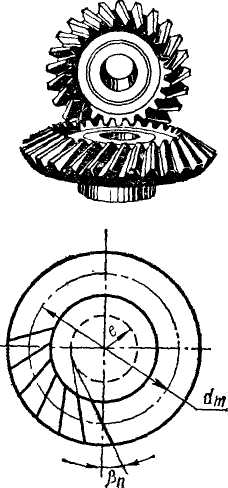
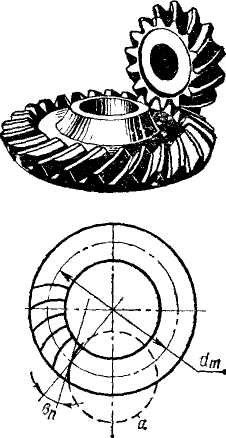
Из различных типов конических колес с непрямыми зубьями на практике получили распространение колеса с косыми или тангенциальными зубьями (рис.4.25) и колеса с круговыми зубьями (рис. 4. 26).
Тангенциальный зуб направлен по касательной к некоторой воображаемой окружности радиусом е и составляет с образующей конуса
|
|
Рис. 4.25 Рис. 4.26
 угол
угол 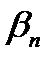 . Круговой зуб располагается по дуге окружности а, по которой движется инструмент при нарезании зубьев. Угол наклона кругового зуба переменный. За расчетный угол принимают угол на окружности среднего диаметра колеса. Значения углов
. Круговой зуб располагается по дуге окружности а, по которой движется инструмент при нарезании зубьев. Угол наклона кругового зуба переменный. За расчетный угол принимают угол на окружности среднего диаметра колеса. Значения углов 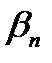 , выполняют до 25. . .30° — для колес с тангенциальным зубом и
, выполняют до 25. . .30° — для колес с тангенциальным зубом и 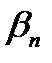
 35° — для колес с круговым зубом.
35° — для колес с круговым зубом.
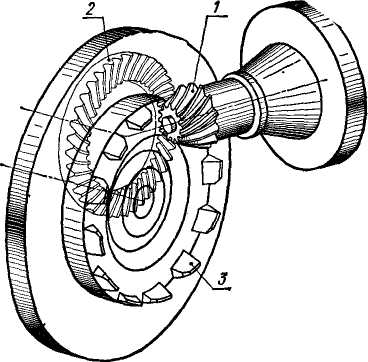
| Рис. 4.27 |
На рис 4.27 показано нарезание кругового конического колеса (1) резцовой головкой (3). Позицией 2 обозначено воображаемое колесо, зубьями которого являются резцы головки.
Расчёт конических передач с непрямыми зубьями ведётся по формулам прямозубых конических передач, но учётом особенностей их геометрии.
4.10 Зубчатые передачи с зацеплением М.Л. Новикова
Эвольвентное зацепление, господствующее пока в современном машиностроении, является линейчатым, т. е. контакт зубьев происходит по по линии ( практически по узкой площадке), расположенной вдоль зуба (рис.4. 28). Вследствие малого приведенного радиуса кривизны контактная прочность эвольвентного зацепления сравнительно невысока, поэтому для современных мощных передач важен вопрос повышения несущей способности зубчатых передач.
|
М. Л. Новиковым было предложено новое точечное зацепление, в котором профили зубьев колес в торцовом сечении очерчены по дугам окружности (рис. 4.30). Зуб шестерни делается выпуклым, а зуб колеса — вогнутым, что увеличивает их приведенный радиус кривизны, значительно повышая контактную прочность передачи.
|
Рис. 4.30. Схема движения Рис. 4.31. Передача Новикова
контактной площадки в
эвольвентном зацеплении
|
| Рис. 4.32. Схема движения контактной площадки в зацеплении Новикова |
В зацеплении Новикова линия контакта зубьев обращается в точку и зубья касаются только в момент прохождения профилей через эту точку (рис. 4.32), а непрерывность передачи движения обеспечивается винтовой формой зубьев. Поэтому зацепление Новикова может быть только косозубым с углом наклона зубьев  β = 10—24°. В результате упругой деформации точечный контакт переходит в контакт по малой площадке. При взаимном перекатывании зубьев контактная площадка перемещается вдоль зуба с большой скоростью, что создает благоприятные условия для образования устойчивого масляного слоя между зубьями. По этой причине потери на трение в передаче Новикова значительно меньше. Зубья колес точечного зацепления нарезают методом обкатки на том же оборудовании, что и при эвольвентном зацеплении, но особым зуборезным инструментом.
β = 10—24°. В результате упругой деформации точечный контакт переходит в контакт по малой площадке. При взаимном перекатывании зубьев контактная площадка перемещается вдоль зуба с большой скоростью, что создает благоприятные условия для образования устойчивого масляного слоя между зубьями. По этой причине потери на трение в передаче Новикова значительно меньше. Зубья колес точечного зацепления нарезают методом обкатки на том же оборудовании, что и при эвольвентном зацеплении, но особым зуборезным инструментом.
Существенным недостатком зацепления Новикова является повышенная чувствительность к изменению межосевого расстояния и к значительным колебаниям нагрузок. Расчет передач с зацеплением Новикова ведется аналогично расчету передач с эвольвентным зацеплением, но с учетом их особенностей.
4.11. Коэффициент полезного действия
К. п. д. зубчатой передачи 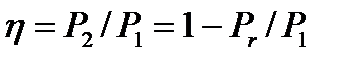 , где Р1, и Р2, — мощности на входе и выходе; Рr — мощность, потерянная в передаче. В свою очередь Рr = Р3 +Pп +Р1. Здесь Р3, Рп, Р1—соответственно мощности, потерянные на трение в зацеплении, трение в подшипниках, разбрызгивание и перемешивание масла (так называемые гидравлические потери).
, где Р1, и Р2, — мощности на входе и выходе; Рr — мощность, потерянная в передаче. В свою очередь Рr = Р3 +Pп +Р1. Здесь Р3, Рп, Р1—соответственно мощности, потерянные на трение в зацеплении, трение в подшипниках, разбрызгивание и перемешивание масла (так называемые гидравлические потери).
Обозначив 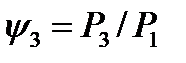 —коэффициент потерь в зацеплении,
—коэффициент потерь в зацеплении, 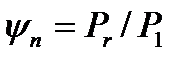 —коэффициент потерь в подшипниках,
—коэффициент потерь в подшипниках, 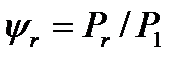 —коэффициент гидравлических потерь, можно записать
—коэффициент гидравлических потерь, можно записать
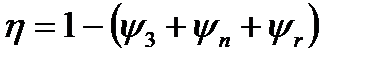 или
или 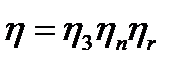
Потери в зацеплении составляют обычно главную часть потерь передачи. Значение 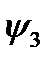 для некорригированных зацеплений можно приближенно оценить по формуле
для некорригированных зацеплений можно приближенно оценить по формуле
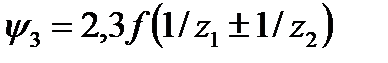 ,
,
где f = 0,06.. .0,1—коэффициент трения в зацеплении; знак « + » для наружного, a «—» для внутреннего зацепления. Средние ориентировочные значения 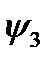 = 0,015.. .0,03. Сумма
= 0,015.. .0,03. Сумма 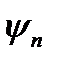 и
и 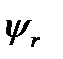 = 0,015.. , . ..0,03.
= 0,015.. , . ..0,03.
Раздельное измерение потерь связано с большими трудностями. Поэтому на практике обычно определяют суммарные потери в передаче. Для приближенных расчетов можно принимать К.П.Д. одной пары зубчатых колёс при густой смазке в пределах 0,94 – 0,96.
4.13 Материалы и термообработка
Практикой эксплуатации и специальными исследованиями установлено, что допускаемая нагрузка по контактной прочности зубьев определяется в основном твёрдостью материала. Наибольшую твёрдость, наименьшие габариты и массу передачи, можно получить при изготовлении зубчатых колес из сталей, подвергнутых термообработке. Сталь в настоящее время — основной материал для изготовления зубчатых колес и в особенности для зубчатых колес высоконагруженных передач. Стали, рекомендуемые для зубчатых колес – это, как правило среднеуглеродистые и легированные конструкционные стали, подвергнутые общей закалке или поверхностной закалке зубьев
-В зависимости от твердости (или термообработки) стальные зубчатые колеса разделяют на две основные группы: твердостью НВ<350 — зубчатые колеса, нормализованные или улучшенные; твердостью НВ>350 — с объемной закалкой, закалкой т. в. ч., цементацией, азотированием и др. Эти группы различны по технологии, нагрузочной способности и способности к приработке.
Твердость материала НВ<350 позволяет производить чистовое нарезание зубьев после термообработки. При этом можно получать высокую точность без применения дорогих отделочных операций (шлифовки, притирки и т. п.). Колеса этой группы хорошо прирабатываются и не подвержены хрупкому разрушению при динамических нагрузках. Для лучшей приработки зубьев твердость шестерни рекомендуют назначать больше твердости колеса не менее чем на 10—15 единиц НВ
Технологические преимущества материала при НВ<350 обеспечили ему широкое распространение в условиях индивидуального и мелкосерийного производства, в мало- и средненагруженных передачах, а также в передачах с большими колесами, термическая обработка которых затруднена.
При НВ>350 (вторая группа материалов) твердость выражается обычно в единицах Роквелла HRC(1HRC 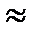 1O HB, точнее см. в справочниках).
1O HB, точнее см. в справочниках).
Специальные виды термообработки позволяют получить HRC до 50. . .60 (НВ<500. . .650). При этом допускаемые контактные напряжения увеличиваются до двух раз, а нагрузочная способность передачи до четырех раз по сравнению с нормализованными или улучшенными сталями. Возрастает также износостойкость и стойкость против заедания.
Применение высокотвердых материалов является большим резервом повышения нагрузочной способности зубчатых передач. Однако с высокой твердостью связаны некоторые дополнительные трудности:
1. Высокотвердые материалы плохо прирабатываются, поэтому они требуют повышенной точности изготовления, повышенной жесткости валов и опор, желательно фланкирование зубьев прямозубых колес.
2. Нарезание зубьев при высокой твердости затруднено, поэтому термообработку выполняют после нарезания. Некоторые виды термообработки (объемная закалка, цементация) сопровождаются значительным короблением зубьев. Для исправления формы зубьев требуются дополнительные операции: шлифовка, притирка, обкатка и т. п. Эти трудности проще преодолеть в условиях крупносерийного и массового производства, когда окупаются затраты на специальное оборудование, инструменты и приспособления. В изделиях крупносерийного и массового производства применяют, как правило, колеса с высокотвердыми зубьями.
Объемная закалка — наиболее простой способ получения высокой твердости зубьев. При этом зуб становится твердым по всему объему. Для объемной закалки используют углеродистые и легированные стали со средним содержанием углерода 0,35. . .0,5% (стали 45, 40Х, 40ХН и т. д.). Твердость на поверхности зуба HRC 45. . .55.
Недостатки объемной закалки: коробление зубьев и необходимость последующих отделочных операций; понижение изгибной прочности при ударных нагрузках (материал приобретает хрупкость). Последнее связано с тем, что для получения необходимой твердости при закалке скорость охлаждения не должна быть ниже критической. С увеличением размеров сечений детали скорость охлаждения падает, и если ее значение будет меньше критической, то получается так называемая мягкая закалка. Мягкая закалка дает пониженную твердость.
Объемную закалку во многих случаях заменяют поверхностными термическими и химико-термическими видами обработки, которые обеспечивают высокую поверхностную твердость (высокую контактную прочность) при сохранении вязкой сердцевины зуба (высокой изгибной прочности при ударных нагрузках).
Поверхностная закалка токами высокой частоты (т. в. ч.) или пламенем ацетиленовой горелки обеспечивает HRC 48. . .54 и применима для сравнительно крупных зубьев (m>5 мм). При малых модулях опасно прокаливание зуба насквозь, что делает зуб хрупким и сопровождается его короблением. При относительно тонком поверхностном закаливании зуб искажается мало. И все же без дополнительных отделочных операций трудно обеспечить степень точности выше 8-й. Закалка т. в. ч. требует специального оборудования и строгого соблюдения режимов обработки. Стоимость обработки т. в. ч. значительно возрастает с увеличением размеров колес. Поэтому большие колеса чаще закаливают с нагревом ацетиленовым пламенем. Для поверхностной закалки используют стали 40Х, 40ХН, 45 и др.
Цементация (насыщение углеродом поверхностного слоя с последующей закалкой) -г- длительный и дорогой процесс. Однако она обеспечивает очень высокую твердость (HRC 58. . .63). При закалке после цементации форма зуба искажается, а поэтому требуются отделочные операции. Для цементации применяют низкоуглеродистые простые стали (сталь 15 и 20) и легированные (20Х, 12ХНЗА и др.). Легированные стали обеспечивают повышенную прочность сердцевины и этим предохраняют продавливание хрупкого поверхностного слоя при перегрузках. Глубина цементации около 0,1. . .0,15 от толщины зуба, но не более 1,5. . .2 мм.
При цементации хорошо сочетаются весьма высокие контактная и изгибная прочности. Ее применяют в изделиях, где масса и габариты имеют решающее значение (транспорт, авиация и т. п.).
Нитроцементация — насыщение углеродом в газовой среде. При этом по сравнению с цементацией сокращаются длительность и стоимость процесса, упрочняется тонкий поверхностный слой — 0,3. . . 0,8 мм до HRС 60. . .63, коробление уменьшается, что позволяет избавиться от последующего шлифования. Нитроцементация удобна в массовом производстве и получила широкое применение в редукторах общего назначения, в автомобилестроении и других отраслях — материалы 25ХГМ, 25ХГТ и др.
Азотирование (насыщение поверхностного слоя азотом) обеспечивает не меньшую твердость, чем при цементации. Малая толщина твердого слоя (около 0,1. . =0,6 мм) делает зубья чувствительными к перегрузкам и непригодными для работы в условиях повышенного абразивного износа (например, плохая защита от загрязнения). Степень коробления при азотировании мала. Поэтому этот вид термообработки особенно целесообразно применять в тех случаях, когда трудно выполнить шлифование зубьев (например, колеса с внутренними зубьями). Для азотируемых колес применяют молибденовую сталь 38ХМЮА или ее заменители 38ХВФЮА и 38ХЮА. Заготовку зубчатого колеса, предназначенного для азотирования, подвергают улучшению в целях повышения прочности сердцевины.
При отсутствии абразивного износа целесообразно применять так называемое мягкое азотирование на глубину 10. . .15 мкм. Оно значительно проще, обеспечивает минимальное коробление и позволяет получать зубья 7-й степени точности без отделочных операций. Для мягкого азотирования применяют улучшенные хромистые стали типа 40Х, 40ХФА, 40Х2НМА.
Как было отмечено, высокая твердость зубьев значительно повышает их контактную прочность. В этих условиях решающей может оказаться не контактная, а изгибная прочность. Для повышения изгибной прочности высокотвердых зубьев рекомендуют проводить упрочнение галтелей путем дробеструйного наклепа, накатки и т. п.
В зависимости от способа получения заготовки различают литые, кованые, штампованные колеса и колеса, изготовляемые из круглого проката. Стальное литье обладает пониженной прочностью и используется обычно для колес крупных размеров, работающих в паре с кованой шестерней.
Чугун применяют главным образом для изготовления крупногабаритных, тихоходных колес и колес открытых зубчатых передач. Основной недостаток чугуна — пониженная прочность по напряжению изгиба. Однако чугун хорошо противостоит усталостному выкрашиванию и заеданию в условиях скудной смазки. Он не дорог и обладает хорошими литейными свойствами, хорошо обрабатывается. Разработанные новые сорта модифицированного чугуна позволяют чугунному литью конкурировать со стальным литьем также и в закрытых передачах. Для изготовления зубчатых колес применяют серый и модифицированный чугун, а также магниевый чугун с шаровидным графитом — см. ГОСТ 1412—79.
Из пластмасс для изготовления зубчатых колес находят применение главным образом текстолит и лигнофоль, а также полиамиды типа капрона. Из пластмассы изготовляют обычно одно из зубчатых колес пары. Из-за сравнительно низкой нагрузочной способности пластмассовых колес их целесообразно применять в малонагруженных и кинематических передачах. В силовых передачах пластмассовые колеса используют только в отдельных случаях, например при необходимости обеспечить бесшумную работу высокоскоростной передачи, не прибегая к высокой точности изготовления и вместе с тем при условии, что габариты этой передачи допускают повышенные размеры колес. Пластмассовые колеса целесообразно применять и в тех случаях, когда трудно обеспечить точное расположение валов (нет общего жесткого корпуса). Эти колеса менее чувствительны к неточностям сборки и изготовления благодаря малой жесткости материала.
4.13. Допускаемые напряжения
Допускаемые контактные напряжения при расчете на усталость.
Расчет на усталость при циклических контактных напряжениях, так же как и при циклических нормальных или касательных напряжениях, базируется на кривых усталости.
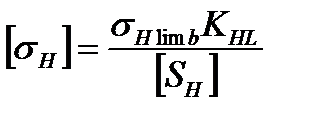 , (4.39)
, (4.39)
где 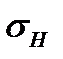 - максимальное напряжение цикла,
- максимальное напряжение цикла, 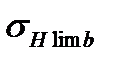 - предел контактной выносливости выносливости при отнулевом цикле напряжений и базовом числе циклов (выбирается по справочникам), Khl—коэффициент долговечности. Если число циклов нагружений каждого зуба колеса больше базового (
- предел контактной выносливости выносливости при отнулевом цикле напряжений и базовом числе циклов (выбирается по справочникам), Khl—коэффициент долговечности. Если число циклов нагружений каждого зуба колеса больше базового ( 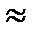 107 ) , то принимают
107 ) , то принимают 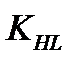 =1. В других случаях, когда эквивалентное число циклов перемены напряжений NHE меньше базового NHO , то
=1. В других случаях, когда эквивалентное число циклов перемены напряжений NHE меньше базового NHO , то 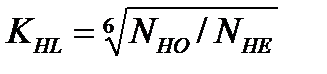 .
.
Если при расчёте колёс из нормализованной или улучшенной стали 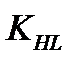 получается больше
получается больше
2,6 , то принимают 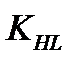 = 2,6. Для колёс из закаленной стали
= 2,6. Для колёс из закаленной стали 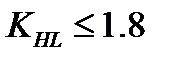 .
.
Коэффициент безопасности 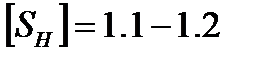 при объёмной закалке и
при объёмной закалке и 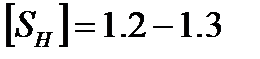 при поверхностной закалке зубьев.
при поверхностной закалке зубьев.
Для прямозубых передач, а также для косозубых с небольшой разностью твердости зубьев шестерни и колеса за расчетное принимается меньшее из двух допускаемых напряжений, определенных для материала шестерни и колеса .
В косозубых передачах зубья шестерни целесообразно выполнять с твердостью, значительно превышающей твердость зубьев колеса (например, шестерня > НВ 400, колесо < НВ 320), потому что зубья шестерни чаще входят в зацепление чем зубья колеса.
Допускаемые напряжения изгиба при расчёте на усталость вычисляются по формуле, аналогичной (4.39), но там значения составляющих принимают по напряжениям изгиба.
4.14 Планетарные передачи
Общие сведения
Планетарными называют передачи, имеющие зубчатые колеса с перемещающимися осями. Наиболее распространенная простейшая однорядная планетарная передача (рис. 4.33) состоит из центрального колеса 1 с наружными зубьями, неподвижного центрального (корончатого) колеса 3 с внутренними зубьями и водила Н, на котором закреплены оси планетарных колес, или сателлитов, 2.
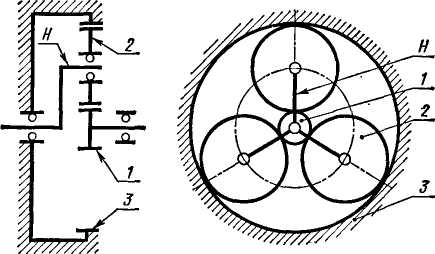
Рис. 4.33. Схема однорядной планетарной передачи
Сателлиты обкатываются по центральным колесам и вращаются вокруг своих осей, т. е. совершают движение, подобное движению планет. Водило вместе с сателлитами вращается вокруг центральной оси.
При неподвижном колесе 3 движение передается от колеса 1 к водилу Н или наоборот.
Если в планетарной передаче сделать подвижными все звенья, т. е. оба колеса и водило, то такую передачу называют дифференциалом. При помощи дифференциала одно движение можно разложить на два или два сложить в одно. Например, движение от колеса 3 можно передавать одновременно колесу 1 и водилу Н или от колес 1 и 3 к водилу Н и т. д.
Достоинства, недостатки и применение планетарных передач
Достоинства: 1. Малые габариты и масса (передача вписывается в размеры корончатого колеса). Это объясняется тем, что мощность передается по нескольким потокам, численно равным числу сателлитов, поэтому нагрузка на зубья в каждом зацеплении уменьшается в несколько раз. 2. Благодаря соосности ведущих и ведомых валов эти передачи удобны для компоновки машин. 3. Планетарные передачи работают с меньшим шумом, чем обычные зубчатые, что связано с меньшими размерами колес и замыканием сил в механизме. При симметричном расположении сателлитов силы в передаче взаимно уравновешиваются. 4. Малые нагрузки на опоры, что упрощает конструкцию опор и снижает потери в них. 5. Планетарный принцип передачи движения позволяет получить большие передаточные отношения при небольшом числе зубчатых колес и малых габаритах.
Недостатки: 1. Повышенные требования к точности изготовления и монтажа передачи.
2. Резкое снижение к. п. д. передачи с ростом передаточного отношения.
Применение. Планетарную передачу применяют как:
а) редуктор в силовых передачах и приборах;
б) коробку перемены передач, передаточное отношение в которой изменяется путем поочередного торможения различных звеньев (например, водила или одного из колес);
в) как дифференциал в автомобилях, тракторах, станках, приборах. Особенно эффективно применение планетарных передач, совмещенных с электродвигателем.
Передаточное отношениеПри определении передаточного отношения планетарной передачи используют метод остановки водила (метод Виллиса). По этому методу всей планетарной передаче мысленно сообщается дополнительное вращение с угловой скоростью водила 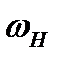 , но в обратном направлении. При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом становятся промежуточными (паразитными) колесами.
, но в обратном направлении. При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом становятся промежуточными (паразитными) колесами.
В качестве примера определения передаточного отношения рассмотрим планетарную передачу, изображенную на рис. 4.33 при передаче движения от колеса 1 к водилу Н.
Для обращенного механизма этой передачи
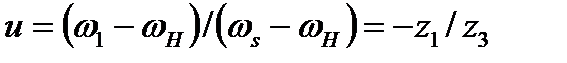 (4.40)
(4.40)
где 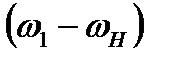 и
и 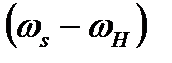 — соответственно угловые скорости колес 1 и 3 относительно водила Н; z1 и z3 — соответственно числа зубьев колес 1 и 3.
— соответственно угловые скорости колес 1 и 3 относительно водила Н; z1 и z3 — соответственно числа зубьев колес 1 и 3.
Здесь существенное значение имеет знак передаточного отношения. Принято передаточное отношение считать положительным, если в обращенном механизме ведущее и ведомое звенья вращаются в одну сторону, и отрицательным, если в разные стороны. В рассматриваемом обращенном механизме колеса 1и 3 вращаются в разные стороны.
Для реальной планетарной передачи, у которой в большинстве случаев колесо 3 закреплено неподвижно, колесо 1 является ведущим, а водило Н — ведомым, из формулы (4.40) при 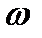 3 = 0 получим
3 = 0 получим
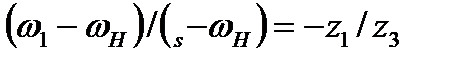 ;
; 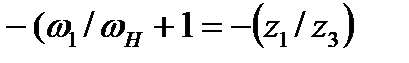
или 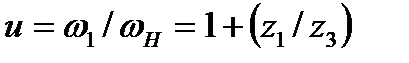 (4.41)
(4.41)
Для других видов планетарных передач передаточное отношение определяется таким же методом.
Разновидности планетарных передач
Существует большое количество различных типов планетарных передач. Выбор типа передачи определяется ее назначением.
Наиболее широко в машиностроении применяется однорядная планетарная передача, схема которой показана на рис. 4.33.
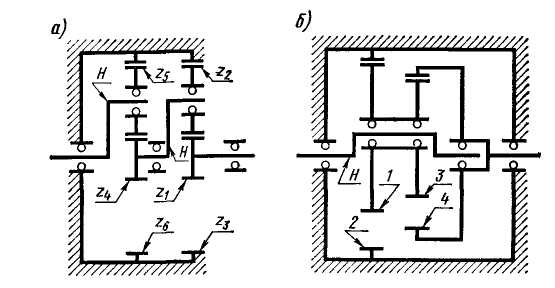
Рис. 4.34. Схема планетарной передачи с двухрядным сателлитом
Эта передача имеет минимальные габариты. Применяется в силовых и вспомогательных приводах. Имеет наиболее высокий К. П. Д. η = 0,96—0,99 при
u = 1,28—8.
Для получения больших передаточных отношений в силовых приводах применяют многоступенчатые планетарные передачи по схеме рис. 4.35, а, представляющие собой последовательное соединение однорядных планетарных передач. В этом случае u =i1*i2 ; 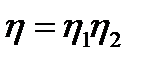
На рис. 4.34,б изображена схема планетарной передачи с двумя внутренними зацеплениями, для которой при передаче движения от водила Н к колесу 4 передаточное отношение
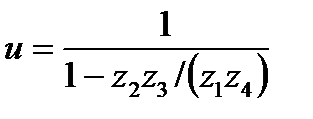 (4.42)
(4.42)
В этой передаче можно получить u> 1600, но при ή < 0,1. Рациональные значения
u = 30—100 при ή = 0,82—0,64. Такую передачу применяют при необходимости получения больших i в случаях, когда к. п. д. не имеет значения (например, в приборах).
Расчет на прочность Расчет на прочность зубьев планетарных передач ведут по формулам обыкновенных зубчатых передач. Расчет выполняют для каждого зацепления. Например, в передаче, изображенной на схеме рис.4.33, необходимо рассчитать внешнее зацепление колес 1и 2 и внутреннее — колес 2 и 3. Так как модули и силы в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочнее внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление.
Выбор числа зубьев колес зависит не только от передаточного отношения u, но и от условия собираемости передачи. По этому условию сумма зубьев центральных колес (z1 + z3) должна быть кратной числу сателлитов С (обычно С = 3—5).
В планетарных передачах применяются не только цилиндрические, но и конические колеса. Зубья могут быть прямые и косые.
4.15 Волновая зубчатая передача
Общие сведения. Волновые зубчатые передачи кинематически представляют собой планетарные передачи с одним гибким зубчатым колесом.
Наиболее распространенная волновая передача (рис. 4.35) состоит из водила Н, вращающегося гибкого колеса 1 с наружными зубьями и неподвижного жесткого колеса 2 с внутренними зубьями.
Водило состоит из овального кулачка и специального шарикоподшипника. Гибкое зубчатое колесо изготовляют в виде стакана с тонкой легко деформирующейся стенкой и соединяют с валом. Длина стакана колеса близка к его диаметру. Жесткое зубчатое колесо соединено с корпусом. Зубья колес чаще всего эвольвентные.
Делительный диаметр d1 гибкого колеса меньше делительного диаметра d2 жесткого колеса на величину d2—dL = s.
Размер овала подшипника качения водила по большой оси больше внутреннего диаметра обода гибкого колеса на величину s.
Сборку зацепления осуществляют после деформирования гибкого колеса водилом. Деформированный зубчатый венец гибкого колеса принимает овальную форму, образуя при этом как бы два сателлита, связанных гибкой стенкой стакана.
Гибкое колесо деформируется так, что на концах большой оси овала зубья зацепляются на полную рабочую высоту. На малой оси
А-А
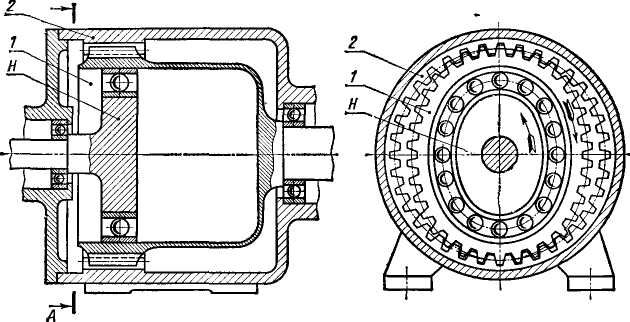
Рис. 4.35. Схема волновой передачи
зубья не зацепляются. Между этими участками зацепление частичное. Из рис. 4.35 следует, что волновая передача может обеспечить одновременное зацепление большого числа зубьев.
| Рис. 4.36. Схема волновой передачи движения в герметизированное простраство |
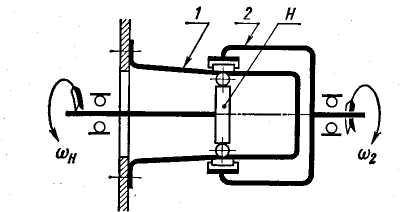 В волновой передаче преобразование движения осуществляется за счет деформирования зубчатого венца гибкого колеса. При вращении водила волна деформации бежит по окружности гибкого зубчатого венца; при этом венец обкатывается в обратномнаправлении по неподвижному жесткому колесу, вращая стакан и вал. Поэтому передача называется волновой, а водило — волновым генератором. При вращении волнового генератора овальной формы образуются две волны. Такую передачу называют двухволновой. Возможны трехволнов ы е передачи.
В волновой передаче преобразование движения осуществляется за счет деформирования зубчатого венца гибкого колеса. При вращении водила волна деформации бежит по окружности гибкого зубчатого венца; при этом венец обкатывается в обратномнаправлении по неподвижному жесткому колесу, вращая стакан и вал. Поэтому передача называется волновой, а водило — волновым генератором. При вращении волнового генератора овальной формы образуются две волны. Такую передачу называют двухволновой. Возможны трехволнов ы е передачи.
Существует много разновидностей волновых передач. Например, для передачи движения через герметическую стенку в химической, авиационной, космической, атомной и других отраслях техники применяют герметическую волновую передачу (рис. 4.36). Здесь гибкий зубчатый венец расположен в середине глухого стакана 1, герметично соединенного с корпусом. Движение передается от генератора волн Н к жесткому колесу 2, соединенному с валом.
Волновая зубчатая передача запатентована в 1959 г. , находится в стадии интенсивного исследования и уже широко применяется в стандартных редукторах малых мощностей .
Достоинства, недостатки и применение волновых передач Достоинства: 1. Способность передавать большие нагрузки, так как в зацеплении одновременно находится большое число зубьев.
2. Возможность передачи движения в герметизированное пространство без применения уплотнений.
3. Большое передаточное отношение при малых габаритах и сравнительно высоком, к. п. д. Для одной ступени u< 300 при К. П. Д. η = 0,8—0,9.
4. Работают с меньшим шумом и обладают высокой демпфирующей способностью.
Недостатки: 1. Сложность изготовления гибкого колеса и генератора.
2. Ограничение угловой скорости вала генератора при больших диаметрах колес (во избежание больших окружных скоростей в ободе генератора).
Передаточное отношение.В волновой передаче разность чисел зубьев колес должна быть равной или кратной числу волн С (как в планетарной передаче — числу сателлитов):
z2 –z1 = C , где z1 и z2 — соответственно числа зубьев гибкого и жесткого колеса.
Передаточное отношение волновых передач определяется так же, как для планетарных, методом остановки водила.
При неподвижном жестком колесе (см. рис. 4.35)
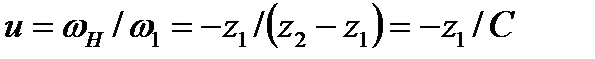 ,(4.43)
,(4.43)
где 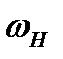 и
и 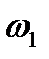 — соответственно угловые скорости волнового генератора и гибкого колеса. Знак минус указывает на разные направления вращения генератора и гибкого колеса.
— соответственно угловые скорости волнового генератора и гибкого колеса. Знак минус указывает на разные направления вращения генератора и гибкого колеса.
При неподвижном гибком колесе (см. рис.4.6)
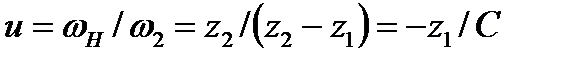 , (4.44)
, (4.44)
где 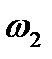 — угловая скорость жесткого колеса.
— угловая скорость жесткого колеса.
Из анализа формул (4.43)—(4.44) следует, что волновая передача может иметь большие u.
Рекомендуется: при стальном гибком колесе u = 60—300; при пластмассовом гибком колесе
u = 20—300.
Расчет волновых передачОдним из критериев работоспособности волновых передач является износ зубьев, который зависит от допускаемых напряжений смятия [σ]см на их рабочих поверхностях. По этому показателю рассчитывают диаметр делительной окружности d гибкого колеса как основной габаритный размер передачи:
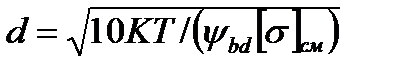
где Т — момент вращения на валу гибкого колеса; К — коэффициент нагрузки, равный 1,25 при умеренной динамической нагрузке, 1,75 — при резко динамической нагрузке; 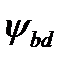 — коэффициент ширины венца (берется 0,18—0,2 для силовых передач; 0,1—0,15 — для приборов).
— коэффициент ширины венца (берется 0,18—0,2 для силовых передач; 0,1—0,15 — для приборов).
В средних условиях [σ]см для стальных колес 10—30 МПа, для пластмассовых 3—5 МПа.
Модуль зацепления m не лимитирует нагрузочной способности передачи и определяется геометрическим путем (обычно m = 0,5 — 1,5 мм).
Подшипники качения генератора волн рассчитывают по динамической грузоподъемности (см. главу «Подшипники качения»).
Дата добавления: 2015-11-28; просмотров: 1493;
