Фрикционные передачи. Фрикционные передачи по форме фрикционных катков могут быть: цилиндрическими, коническими, лобовыми - с внешним и внутренним контактом
Фрикционные передачи по форме фрикционных катков могут быть: цилиндрическими, коническими, лобовыми - с внешним и внутренним контактом. Главное достоинство фрикционных передач заключается в возможности создания на их базе фрикционных вариаторов (бесступенчатых коробок передач), а также в бесшумной их работе при высоких скоростях.
ГЛАВА ΙV.
Зубчатые передачи
4.1.Общие сведения
В курсе «Детали машин» изучают методы расчета зубчатых передач на прочность. При этом предполагается, что из курса «Теория механизмов» изучающим известны расчеты геометрии зацепления и способы изготовления зубчатых колес. Некоторые сведения по этим вопросам излагаются в курсе «Детали машин» в том объеме, какой необходим для уяснения основных
| Рис. 4.1 |
Принцип действия и
| Рис.4.1 |
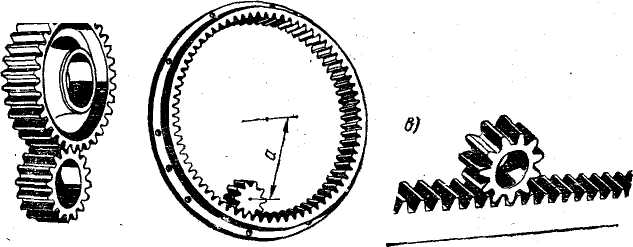
По расположению осей валов различают: передачи с параллельными осями, которые выполняют с цилиндрическими коле-сами внешнего или внутреннего зацепления, рис. 4.1 а, б; передачи с пересекающимися осями — конические колеса, см. рис. 8.29; передачи с пересекающимися осями — цилиндрические винтовые, см. рис. 8.56, конические гипоидные, см. рис. 8.57, червячные, см. рис. 9.1. Кроме того, применяют передачи между зубчатым колесом и рейкой, рис. 8.2, в.
По расположению зубьев на колесах различают передачи: прямозубые и косозубые.
По форме профиля зуба различают: эвольвентные и круговые. Наиболее распространен эвольвентный профиль зуба, предложенный Эйлером в 1760 г. Он обладает рядом существенных технологических и эксплуатационных преимуществ. Круговой профиль зуба предложен М. Л. Новиковым в 1954 г. По сравнению с эвольвентным он позволяет повысить нагрузку передач.
Оценка и применение.
Основные преимущества зубчатых передач: высокая нагрузочная способность как следствие, малые габариты,
большая долговечность и надежность работы (например, для редукторов общего применения установлен ресурс ~30 000 ч); высокий к. п. д. (до 0,97...0,98 в одной ступени); постоянство передаточного отношения (отсутствие проскальзывания); возможность применения в широком диапазоне скоростей (до 150 м/с), мощностей (до десятков тысяч кВт) и передаточных отношений (до нескольких сотен и даже тысяч).
Среди недостатков зубчатых передач можно отметить повышенные требования к точности изготовления, шум при больших скоростях, высокую жесткость, не позволяющую компенсировать динамические нагрузки. Отмеченные недостатки не снижают существенного преимущества зубчатых передач перед другими. Вследствие этого зубчатые передачи наиболее широко распространены во всех отраслях машиностроения и приборостроения. Из всех перечисленных выше разновидностей зубчатых передач наибольшее распространение имеют передачи с цилиндрическими колесами, как наиболее простые в изготовлении и эксплуатации, надежные и малогабаритные. Конические, винтовые и червячные передачи применяют лишь в тех случаях, когда это необходимо по условиям компоновки машины.
4.2. Краткие сведения о геометрии и кинематике
Все понятия и термины, относящиеся к геометрии и кинематике зубчатых передач, стандартизованы. Стандарты устанавливают термины, определения и обозначения, а также методы расчета геометрических параметров.
Основные параметры.
Меньшее из пары зубчатых колес называют шестерней, а большее — колесом. Термин «зубчатое колесо» является общим. Параметрам шестерни приписывают индекс 1, а параметрам колеса — 2 (рис. 4.2). Кроме того, различают индексы, относящиеся: w — к начальной поверхности или окружности; b — к основной поверхности или окружности; а — к поверхности или окружности вершин и головок зубьев; f — к поверхности или окружности, впадин и ножек зубьев. Параметрам, относящимся к делительной поверхности или окружности, дополнительного индекса не приписывают.
| Рис. 4.2 |
 Общие понятия о параметрах пары зубчатых колес и их взаимосвязи проще всего уяснить, рассматривая прямозубые колеса. При этом особенности косозубых колес рассматривают дополнительно. z1 и z2— число зубьев шестерни и колеса; u=z1/z2 — передаточное число (отношение большего числа зубьев к меньшему, которое используется наряду с передаточным отношением i=n1/n2, как более удобное при расчете по контактным напряжениям; р — делительный окружной шаг зубьев (равный шагу исходной зубчатой рейки); рb=p cosa — основной окружной шаг зубьев; a — угол профиля делительный (равный углу профиля исходного контура), по ГОСТ 13755 a=2О°;
Общие понятия о параметрах пары зубчатых колес и их взаимосвязи проще всего уяснить, рассматривая прямозубые колеса. При этом особенности косозубых колес рассматривают дополнительно. z1 и z2— число зубьев шестерни и колеса; u=z1/z2 — передаточное число (отношение большего числа зубьев к меньшему, которое используется наряду с передаточным отношением i=n1/n2, как более удобное при расчете по контактным напряжениям; р — делительный окружной шаг зубьев (равный шагу исходной зубчатой рейки); рb=p cosa — основной окружной шаг зубьев; a — угол профиля делительный (равный углу профиля исходного контура), по ГОСТ 13755 a=2О°;
aw – угол зацепления или угол профиля начальный, cos aw=a cos a/aw;
m=p/π — окружной модуль зубьев (основная характеристика размеров зубьев). Значения модулей стандартизованы в диапазоне 0,05...100 мм (табл. 4.1);
d=pz/π =mz — делительный диаметр
Таблица 4.1
| Ряды Модуль, мм 1-й 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25 2-й 1,125; 1,375; 1,75; 2,25; 2,75; 3,5 4,5; 5,5 ; 7 ; 9; 11; 14; 18; 22 |
Примечание. Следует предпочитать 1-й ряд
(диаметр окружности, по которой обкатывается инструмент при нарезании); db=d cosa— основной диаметр (диаметр окружности, разверткой которой являются эвольвенты зубьев); dw1 и dw2 — начальные диаметры (диаметры окружностей, по которым пара зубчатых колес обкатывается в процессе вращения):
dw1=2aw /(u+1), dw1=2aω—dwl.
У передач без смещения и при суммарном смещении 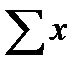 (см. ниже) начальные и делительные окружности совпадают:
(см. ниже) начальные и делительные окружности совпадают:
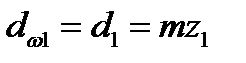 ;
; 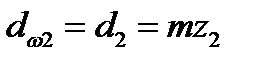 .
.
При нарезании колес со смещением делительная плоскость рейки (делительная окружность инструмента) смещается к центру или от центра заготовки на хт (см. рис. 4.14  ); х — коэффициент смещения исходного контура. Смещение от центра считается положительным (x>0), а к центру — отрицательным (x<0).
); х — коэффициент смещения исходного контура. Смещение от центра считается положительным (x>0), а к центру — отрицательным (x<0).
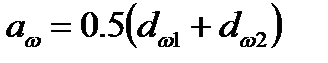 —межосевое расстояние;
—межосевое расстояние;
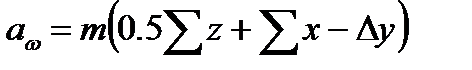 ,
,
Где , 
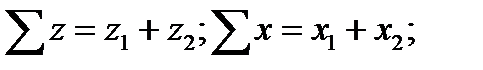
 y—коэффициент уравнительного смещения при
y—коэффициент уравнительного смещения при 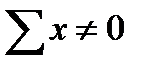 (определяется по ГОСТ 16532, ) для передач без смещения и при
(определяется по ГОСТ 16532, ) для передач без смещения и при  или x1=x2 или
или x1=x2 или 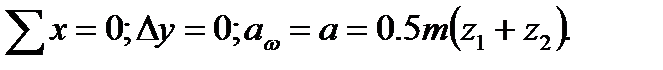
h= m(2ha* +c*-  y) –высота зуба; da = d + 2m (ha*+x-
y) –высота зуба; da = d + 2m (ha*+x-  y) —диаметр вершин зубьев;
y) —диаметр вершин зубьев;
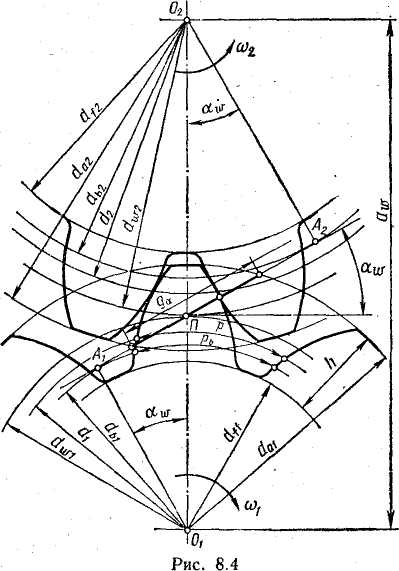
df = d-2m(h*a+c*—x) - диаметр впадин; h*a—коэффициент высоты головки зуба (по ГОСТ 13755 h*a =l); с*—коэффициент радиального зазора (по ГОСГ 13755 - с* = 0,25). Для колес без смещения h = 2,25m; da = d – 2m; df = d—2,5m; A1A2—линия зацепления (общая касательная к основным окружностям); ga—длина активной линии зацепления (отсекаемая ок-ружностями вершин зубьев); П — полюс зацепления (точка касания начальных окружности и одновременно точка пересечения линии центров колес O1O2 с линией зацепления).
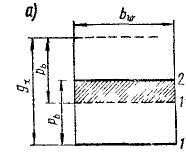
Коэффициент терцового перекрытия έa и изменение нагрузкипо профилю зуба. При вращении колес (см. рис. 4.3) линия контакта зубьев перемещается в поле зацепления (рис. 4.5,а), у которого одна сторона равна длине активной линии зацепления ga,
|
| Рис. 4.3 |
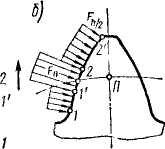 а другая — рабочей ширине зубчатого венца bw. Пусть линия контакта первой пары зубьев находится в начале поля зацепления, тогда при рь < ga в поле зацепления находится еще и линия контакта 2 второй пары зубьев. При вращении колес линии 1 и 2 перемещаются в направлении, указанном стрелкой. Когда вторая пара придет
а другая — рабочей ширине зубчатого венца bw. Пусть линия контакта первой пары зубьев находится в начале поля зацепления, тогда при рь < ga в поле зацепления находится еще и линия контакта 2 второй пары зубьев. При вращении колес линии 1 и 2 перемещаются в направлении, указанном стрелкой. Когда вторая пара придет
на границу поля 2', первая пара займет положение 1'. При дальнейшем движении на участке 1'.. .2 зацепляется только одна пара зубьев. Однопарное зацепление продолжается до rex пор, пока пара / не займет положение 2. В этот момент в зацепление вступит следующая пара зубьев и снова начнется двухпарное зацепление.
| 6) |
Переходя от поля зацепления к профилю зуба (рис. 4.4), можно отметить, что зона однопарного зацепления 1...2 располагается посредине зуба или в районе полюса зацепления (см. также рис. 4.2). В зоне однопарного зацепления зуб передает полную нагрузку Fn, а в зонах двухпарного зацепления (приближенно) только половину 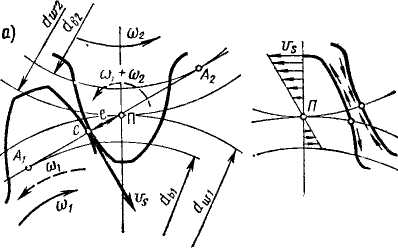 нагрузки. Размер зоны
нагрузки. Размер зоны
однопарного зацепления зависит от значения коэффициента торцового перекрытия 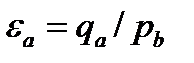 .
.
| Рис.4.4 |
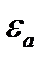 > 1 .
> 1 .
Скольжение и трение в зацеплении. В точках контакта С
наблюдается (рис. 4.4, а) перекатывание и скольжение зубьев. Скорость скольжения пропорциональна расстоянию е точки контакта от полюса. В полюсе она равна нулю, а при переходе через полюс меняется знак. Переходя от линии зацепления к поверхности зубьев (рис. 4.4, б), отметим, что максимальное скольжение наблюдается на ножках и головках зубьев, на начальной окружности оно равно нулю и изменяет направление. Скольжение сопровождается трением. Трение является причиной потерь в зацеплении и износа зубьев. У ведущих зубьев силы трения направлены от начальной окружности, а у ведомых — наоборот. При постоянных диаметрах колес расстояние точек начала и конца зацепления от полюса, и, следовательно, скорость скольжения увеличиваются с увеличением высоты зуба и модуля зацепления. У мелкомодульных колес с большим числом зубьев скольжение меньше, а к. п. д. выше, чем у крупномодульных с малым числом зубьев .
Точность изготовления и ее влияние на качество передачи. Качество передачи связано с ошибками изготовления зубчатых колес и деталей (корпусов, подшипников и валов), определяющих их взаимное расположение. Деформация деталей под нагрузкой также влияет на качество передачи. Основными ошибками изготовления зубчатых колес являются: ошибка шага и формы профиля зубьев, ошибки в направлении зубьев относительно образующей делительного цилиндра.
Ошибки шага и профиля нарушают кинематическую точность и плавность работы передачи. В передаче сохраняется постоянным только среднее значение передаточного отношения u. Мгновенные значения u в процессе вращения периодически изменяются. Колебания передаточного отношения особенно нежелательны в кинематических цепях, выполняющих следящие, делительные и измерительные функции (станки, приборы и др.). В силовых быстроходных передачах с ошибками шага и профиля связаны дополнительные динамические нагрузки, удары и шум в зацеплении.
Ошибки в направлении зубьев в сочетании с перекосом валов вызывают неравномерное распределение нагрузки по длине зуба.
Точность изготовления зубчатых передач регламентируется стандартом, который предусматривает 12 степеней точности. Каждая степень точности характеризуется тремя показателями: 1) нормой кинематической точности, регламентирующей наибольшую погрешность передаточного отношения или полную погрешность угла поворота зубчатого колеса в пределах одного оборота (в зацеплении с эталонным колесом); 2) нормой плавности работы, регламентирующей многократно повторяющиеся циклические ошибки, передаточного отношения или угла поворота в пределах одного оборота; 3) нормой контакта зубьев, регламентирующей ошибки изготовления зубьев и сборки передачи, влияющие на размеры пятна контакта в зацеплении (распределение нагрузки по длине зубьев).
Степень точности выбирают в зависимости от назначения и условий работы передачи. Наибольшее распространение имеют 6, 7 и 8-я степени точности.
Стандарт допускает комбинацию степеней точности по отдельным нормам. Например, для тихоходных высоконагруженных передач можно принять повышенную норму контакта зубьев по сравнению с другими нормами, а для быстроходных малонагруженных — повышенную норму плавности и т. п.
Во избежание заклинивания зубьев в зацеплении должен быть боковой зазор. Размер зазора регламентируется видом сопряжения зубчатых колес. Стандартом предусмотрено шесть видов сопряжения: И — нулевой зазор; Е — малый зазор; С и D — уменьшенный зазор; В — нормальный зазор; А — увеличенный зазор. При сопряжениях Н, Е и С требуется повышенная точность изготовления. Их применяют для реверсируемых передач при высоких требованиях к кинематической точности, а также при наличии крутильных колебаний валов.
Стандарт устанавливает также допуски на межосевые расстояния, перекос валов и некоторые другие параметры.
4.3. Контактные напряжения и контактная прочность
Контактные напряжения образуются в месте соприкосновения двух тел в тех случаях, когда размеры площадки касания малы по сравнению с размерами тел (сжатие двух шаров, шара и плоскости, двух цилиндров и т. п.). Если значение контактных напряжений больше допускаемого, то на поверхности деталей появляются вмятины, борозды, трещины или мелкие раковины. Подобные повреждения наблюдаются у зубчатых, червячных, фрикционных и цепных передач, а также в подшипниках качения.
Теория контактных напряжений является предметом курса «Теория упругости». Расчеты многих деталей машин, изучаемые в данном курсе, выполняют по контактным напряжениям. Поэтому ниже излагаются краткие сведения о контактных напряжениях и о разрушениях деталей, связанных с этими напряжениями.
При расчете контактных напряжений различают два характерных случая: первоначальный контакт в точке (два шара, шар и плоскость и т. п.); первоначальный контакт по линии (два цилиндра с параллельными осями, цилиндр и плоскость и т. п.).
На рис. 4.5 изображен пример сжатия двух цилиндров с параллельными осями. До приложения удельной нагрузки q цилиндры соприкасались по линии. Под нагрузкой линейный контакт переходит в контакт по узкой площадке. При этом точки максимальных нормальных напряжений ан располагаются на продольной оси симметрии контактной площадки. Значение этих напряжений вычисляют по формуле
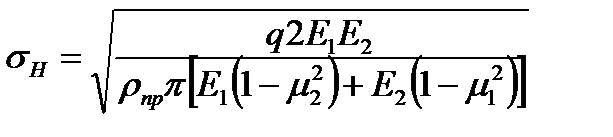 (4.1)
(4.1)
Для конструкционных металлов коэффициент Пуассона располагается в пределах μ=0,25...0,35. Без существенной погрешности принимают μ1 = μ2 = 0,3 и получают
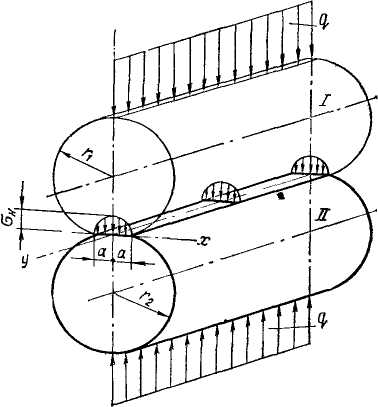
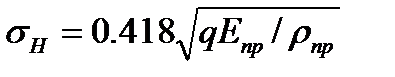 (4.2)
(4.2)
Здесь 1/рпр=1/ρ1±1/ρ2, Eпр = 2E1E2 /(E1 +E2) (4.3)
 где Епр и рпр — приведенные модуль упругости и радиус кривизны; Е1 Е2, р1 р2—модули упругости и радиусы цилиндров. (Основоположником теории контактных напряжений является Н. Herz (1881). В его честь приписывают индекс Н обозначениям контактных напряжений).
где Епр и рпр — приведенные модуль упругости и радиус кривизны; Е1 Е2, р1 р2—модули упругости и радиусы цилиндров. (Основоположником теории контактных напряжений является Н. Herz (1881). В его честь приписывают индекс Н обозначениям контактных напряжений).
Формула (4.2) справедлива не только для круговых, но и для любых других цилиндров. Для последних r1 и г2— радиусы кривизны в точках контакта. При контакте цилиндра с плоскостью r2= 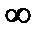 . Знак минус в формуле (4.3) относится к случаю внутреннего контакта (когда поверхность одного из цилиндров вогнутая).
. Знак минус в формуле (4.3) относится к случаю внутреннего контакта (когда поверхность одного из цилиндров вогнутая).
| Рис. 4.5 |
| в) |
| Рис.4.6 |
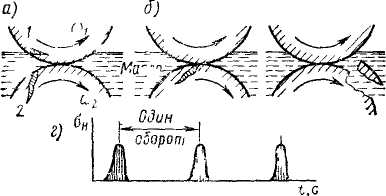 прохождения зоны контакта и свободна от напряжений в остальное время оборота цилиндра. Переменные контактные напряжения вызывают усталость поверхностных слоев деталей. На поверхности образуются микротрещины с последующим выкрашиванием мелких частиц металла. Если детали работают в масле, то оно проникает в микротрещины (рис. 4.6, а). Попадая в зону контакта (рис. 4.6, б), трещина закрывс1ется, а заполняющее ее масло подвергается высокому давлению. Это давление способствует развитию трещины до тех пор, пока не произойдет выкрашивание частицы металла (рис. 4,6, в) Выкрашивание не наблюдается, если значение контактных напряжений не превышает допускаемого
прохождения зоны контакта и свободна от напряжений в остальное время оборота цилиндра. Переменные контактные напряжения вызывают усталость поверхностных слоев деталей. На поверхности образуются микротрещины с последующим выкрашиванием мелких частиц металла. Если детали работают в масле, то оно проникает в микротрещины (рис. 4.6, а). Попадая в зону контакта (рис. 4.6, б), трещина закрывс1ется, а заполняющее ее масло подвергается высокому давлению. Это давление способствует развитию трещины до тех пор, пока не произойдет выкрашивание частицы металла (рис. 4,6, в) Выкрашивание не наблюдается, если значение контактных напряжений не превышает допускаемого
| Рис. 4.7 |
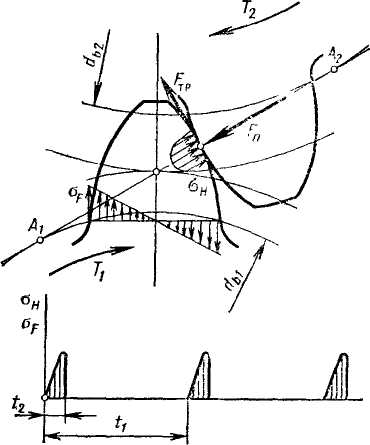 Экспериментально установлено, что при качении со скольжениемцилиндры I и 2 обладают различным сопротивлением усталости. Это объясняется следующим. Усталостные микротрещины при скольжении располагаются не радиально, а вытягиваются в направлении сил трения. При этом в зоне контакта масло выдавливается из трещин опережающего цилиндра и запрессовывается в трещины отстающего цилиндра 2. Поэтому отстающий цилиндр обладает меньшим сопротивлением усталости. Ускорение развития трещин при работе в масле не означает, что без масла разрушение рабочих поверхностей замедлено. Во-первых, масло образует на поверхности защитные пленки, которые частично или полностью устраняют непосредственный металлический контакт и уменьшают трение. При контакте через масляную пленку контактные напряжения уменьшаются, срок службы до зарождения трещин увеличивается. Во-вторых, при работе без масла увеличивается интенсивность абразивного износа, который становится главным критерием работоспособности и существенно сокращает срок службы.
Экспериментально установлено, что при качении со скольжениемцилиндры I и 2 обладают различным сопротивлением усталости. Это объясняется следующим. Усталостные микротрещины при скольжении располагаются не радиально, а вытягиваются в направлении сил трения. При этом в зоне контакта масло выдавливается из трещин опережающего цилиндра и запрессовывается в трещины отстающего цилиндра 2. Поэтому отстающий цилиндр обладает меньшим сопротивлением усталости. Ускорение развития трещин при работе в масле не означает, что без масла разрушение рабочих поверхностей замедлено. Во-первых, масло образует на поверхности защитные пленки, которые частично или полностью устраняют непосредственный металлический контакт и уменьшают трение. При контакте через масляную пленку контактные напряжения уменьшаются, срок службы до зарождения трещин увеличивается. Во-вторых, при работе без масла увеличивается интенсивность абразивного износа, который становится главным критерием работоспособности и существенно сокращает срок службы.
Кривые усталости материала по контактным напряжениям подобны кривым усталости по напряжениям изгиба, растяжения — сжатия и другим (см. курс «Сопротивление материалов»)
4.4. Критерии работоспособности и расчета
Условия работы зуба в зацеплении. При передаче крутящего момента (рис. 4.4) в зацеплении кроме нормальной силы Fn действует сила трения Fтр=Fnf, связанная со скольжением. Под действием этих сил зуб находится в сложном напряженном состоянии (рис. 4.7).
Решающее влияние на его работоспособность оказывают два основных напряжения: контактные напряжения σн и напряжения изгиба σF. Для каждого зуба σн и σF не являются постоянно действующими. Они изменяются во времени по некоторому прерывистому отнулевому циклу (см. рис. 8.9). Время действия σF за один оборот колеса (t1) равно продолжительности зацепления одного зуба (t2). Напряжения σF действуют еще меньшее время. Это время равно продолжительности пребывания в зацеплении данной точки поверхности зуба с учетом зоны распространения контактных напряжений.
Переменные напряжения являются причиной усталостного разрушения зубьев: поломка зубьев от напряжений изгиба и выкрашивание поверхности от контактных напряжений. С контактными напряжениями и трением в зацеплении связаны также износ, заедание и другие виды повреждения поверхностей зубьев.
| Рис. 4.8 |
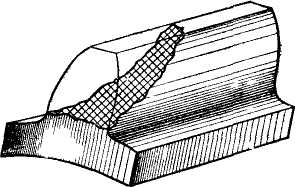 Поломка зубьев (рис. 4.8). Поломка связана с напряжениями изгиба. На практике наблюдается выламывание углов зубьев вследствие концентрации нагрузки. Различают два вида поломки зубьев: поломка от больших перегрузок ударного или даже статического действия (предупреждают защитой привода от перегрузок или учетом перегрузок при расчете); усталостная поломка, происходящая от действия переменных напряжений в течение сравнительно длительного срока службы (предупреждают определением размеров из расчета на усталость). Особое значение имеют меры по устранению концентраторов напряжений (рисок от обработки, раковин и трещин в отливках, микротрещин от термообработки и т. п.). Общие меры предупреждения поломки зубьев — увеличение модуля, положительное смещение при нарезании зубьев,- термообработка, наклеп, уменьшение концентрации нагрузки по краям (жесткие валы, зубья со срезанными углами и пр.).
Поломка зубьев (рис. 4.8). Поломка связана с напряжениями изгиба. На практике наблюдается выламывание углов зубьев вследствие концентрации нагрузки. Различают два вида поломки зубьев: поломка от больших перегрузок ударного или даже статического действия (предупреждают защитой привода от перегрузок или учетом перегрузок при расчете); усталостная поломка, происходящая от действия переменных напряжений в течение сравнительно длительного срока службы (предупреждают определением размеров из расчета на усталость). Особое значение имеют меры по устранению концентраторов напряжений (рисок от обработки, раковин и трещин в отливках, микротрещин от термообработки и т. п.). Общие меры предупреждения поломки зубьев — увеличение модуля, положительное смещение при нарезании зубьев,- термообработка, наклеп, уменьшение концентрации нагрузки по краям (жесткие валы, зубья со срезанными углами и пр.).
Повреждение поверхности зубьев. Все виды повреждения поверхности зубьев (рис. 4.9) связаны с контактными напряжениями и трением.
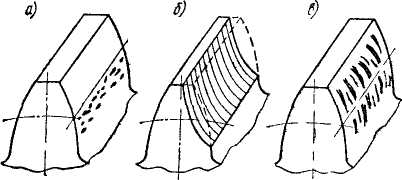 Усталостное выкрашивание от контактных напряжений является основным видом разрушения поверхности зубьев при хорошей смазке передачи (чаще всего это бывают). Зубья таких
Усталостное выкрашивание от контактных напряжений является основным видом разрушения поверхности зубьев при хорошей смазке передачи (чаще всего это бывают). Зубья таких
| Рис. 4.9 |
передач разделены тонким слоем масла, устраняющим металлический контакт. При этом износ зубьев мал. Передача работает длительное время до появления усталости в поверхностных слоях зубьев. На поверхности появляются небольшие углубления, напоминающие оспинки, которые растут и превращаются в раковины. Выкрашивание (рис. 4.9.а) начинается обычно вблизи полюсной линии на ножках зубьев там, где нагрузка передается одной парой зубьев, а скольжение и перекатывание зубьев направлены так, что масло запрессовывается в трещины и способствует выкрашиванию частиц металла. При выкрашивании нарушаются условия образования сплошной масляной пленки, появляется металлический контакт с последующим быстрым износом или задиром поверхности. Образование первых усталостных раковин не всегда служит признаком близкого полного разрушения зубьев. В передачах, зубья которых имеют невысокую твердость (НВ<350), наблюдаются случаи так называемого ограниченного или начального выкрашивания. Начальное выкрашивание связано с приработкой зубьев недостаточно точно изготовленных передач. Оно появляется в местах концентрации нагрузки после непродолжительной работы и затем приостанавливается. При этом образовавшиеся раковины не развиваются и даже совершенно исчезают вследствие сглаживания. Прекращение дальнейшего выкрашивания в этом случае объясняется тем, что разрушение мест концентрации нагрузки выравнивает ее распределение по поверхности зуба. При высокой твердости зубьев (НВ>350) явление ограниченного выкрашивания обычно не наблюдается. Образовавшиеся раковины быстро растут вследствие хрупкого разрушения их краев.
В передачах, работающих со значительным износом, выкрашивание не наблюдается, так как поверхностные слои снимаются раньше, чем появляются трещины усталости.
Основные меры предупреждения выкрашивания: определение размеров из расчета на усталость по контактным напряжениям; повышение твердости материала путем термообработки; повышение степени точности и в особенности по норме контакта зубьев.
Абразивный износ (рис. 4.9, б) является основной причиной выхода из строя передач при плохой смазке. К таким передачам относятся прежде всего открытые передачи, а также закрытые, но недостаточно защищенные от загрязнения абразивными частицами (пыль, продукты износа и т. п.). Такие передачи можно встретить в сельскохозяйственных и транспортных машинах, горнорудном оборудовании, грузоподъемных машинах и т. п. У изношенной передачи увеличиваются зазоры в зацеплении, появляется шум, возрастают динамические нагрузки. В то же время прочность изношенного зуба понижается вследствие уменьшения площади его поперечного сечения. Все это может привести к поломке зубьев, если зубчатые колеса своевременно не забраковать.
Расчет на износ затруднен тем, что интенсивность износа зависит от многих случайных факторов и, в первую очередь, от интенсивности загрязнения смазки.
Основные меры предупреждения износа — повышение твердости поверхности зубьев, защита от загрязнения, применение специальных масел.
Заедание (рис. 4.9,в) наблюдается преимущественно в высоконагруженных и высокоскоростных передачах. В месте соприкасания зубьев этих передач развивается высокая температура, способствующая разрыву масляной пленки и образованию металлического контакта. Здесь происходит как бы сваривание частиц металла с последующим отрывом их от менее прочной поверхности. Образовавшиеся наросты задирают рабочие поверхности зубьев в направлении скольжения. Кромочный удар (см. ниже) способствует заеданию.
Меры предупреждения заедания — те же, что и против износа. Желательно фланкирование зубьев и интенсивное охлаждение смазки. Эффективно применение противозадирных масел с повышенной вязкостью и химически активными добавками. Правильным выбором сорта масла можно поднять допускаемую нагрузку по заеданию над допускаемыми нагрузками по другим критериям.
Пластические сдвиги наблюдаются у тяжелонагруженных тихоходных зубчатых колес, выполненных из мягкой стали. При перегрузках на мягкой поверхности зубьев появляются пластические деформации с последующим сдвигом в направлении скольжения (см. рис. 4.4). В результате у полюсной линии зубьев ведомого колеса образуется хребет, а у ведущего — соответствующая канавка. Образование хребта нарушает правильность зацепления и приводит к разрушению зубьев Пластические сдвиги можно устранить повышением твердости рабочий поверхностей зубьев.
Отслаивание твердого поверхностного слоя зубьев, подвергнутых поверхностному упрочнению (азотирование, цементирование, закалка Т. В. Ч. и т. п.). Этот вид разрушения наблюдается при недостаточно высоком качестве термической обработки, когда внутренние напряжения не сняты отпуском или когда хрупкая корка зубьев не имеет под собой достаточно прочной сердцевины. Отслаиванию способствуют перегрузки.
Из всех перечисленных видов разрушения поверхности зубьев наиболее изучено выкрашивание. Это позволило выработать нормы допускаемых контактных напряжений, устраняющих выкрашивание в течение заданного срока службы. Расчеты по контактным напряжениям, предупреждающие выкрашивание, получили широкое pacnpостранение.
Специальные методы расчета для предупреждения других видов разрушения поверхности зубьев или еще не разработаны (при пластическом сдвиге, отслаивании), или недостаточно разработаны (при износе, заедании), а поэтому здесь не рассматриваются. Поскольку упомянутые нормы допускаемых контактных напряжений проверяют опытом эксплуатации передач, то приближенно можно полагать, что эти нормы учитывают кроме выкрашивания и другие виды повреждения поверхности зубьев. При этом рекомендуют выполнять указанные меры предупреждения повреждений.
В современной методике расчета из двух напряжений σн и аF за основные в большинстве случаев приняты контактные напряжения, так как в пределах заданных габаритов колес σн остаются постоянными, a σF можно уменьшать путем увеличения модуля.
4.5. Расчетная нагрузка 
За расчетную нагрузку принимают максимальное значение удельной нагрузки, распределенной по линии контакта зубьев:
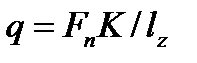 (4.4)
(4.4)
где Fn—нормальная сила в зацеплении; K = KbKV —коэффициент расчетной нагрузки;
Kb—коэффициент концентрации нагрузки; Kv—коэффициент динамической нагрузки;
lz—суммарная длина линии контакта зубьев.
Концентрация нагрузки и динамические нагрузки различно влияют на прочность по контактным и изгибным напряжениям. Соответственно различают KH, KHβ, Khv при расчетах по контактным напряжениям и КF, КFβ  , КF V —по напряжениям изгиба.
, КF V —по напряжениям изгиба.
Коэффициент концентрации нагрузки Kb. Концентрация или неравномерность распределения нагрузки по длине зуба связана с деформацией валов, корпусов, опор и самих зубчатых колес, а также с погрешностями изготовления монтажа передачи.
Коэффициент динамической нагрузки KV. Данный коэффициент учитывает погрешности в изготовлении зубьев колёс по шагу и профилю, которые явно непропорционально проявляются с увеличением частоты вращения колёс (окружной скорости).
Точный расчёт данных коэффициентов довольно сложен и их рекомендуется выбирать из справочной литературы по расчёту зубчатых передач.
4.6. Расчёт прямозубых цилиндрических передач на прочность
Расчёт на прочность прямозубых и косозубых цилиндрических передач стандартизирован ГОСТ 21354. В данном конспекте лекций введены некоторые упрощения, мало влияющие на результаты расчётов для большинства практических случаев.
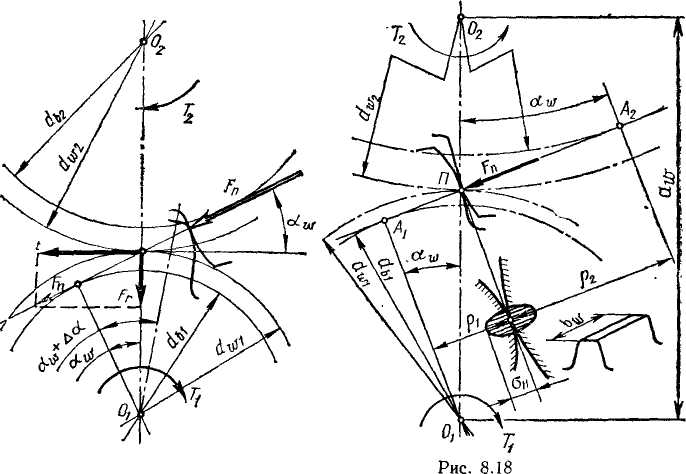
Силы в зацеплении.На рис. 4.10 нормальная сила Fn , направлена по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. При этом силу Fn переносят в полюс и раскладывают на окружную Ft и радиальную Fr . Такое разложение удобно при последующем расчёте валов и опор. По заданным крутящему моменту Т и диаметру зубчатого колеса d определяют окружную силу : 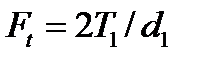 (4.5)
(4.5)
И через неё выражают все остальные составляющие:
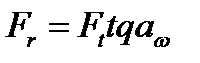 ;
; 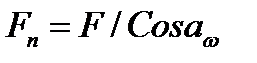 (4.6)
(4.6)
Расчет прочности зубьев по контактным напряжениям.Исследованиями установлено, что наименьшей контактной усталостью обладает околополюсная зона рабочей поверхности зубьев, где наблюдается однопарное зацепление — см. рис. 8.5. Поэтому расчет контактных
напряжений принято выполнять при контакте в полюсе зацепления (рис. 4.3). Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусами р1 и р2. При этом контактные напряжения определяют по формуле (4.2), а именно: 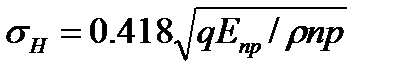 (4.7)
(4.7)
| Рис 4.11 |
| Рис 4.10 |
q = FnKH/bw = FtKH/(bw cos aw) = 2T1KH/(dwlbw cos aw). (4.8)
Радиусы кривизны эвольвент зубьев в точке контакта (см. рис. 8.11):
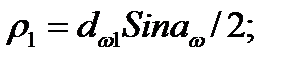
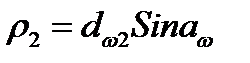
По формуле (4.3):
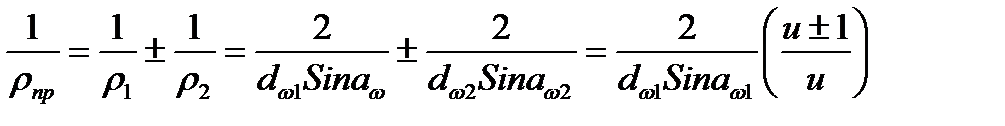 (4.9)
(4.9)
Где 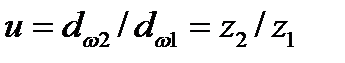 , знак «+» для наружного, а «—» для внутреннего зацепления.
, знак «+» для наружного, а «—» для внутреннего зацепления.
Подставляя в формулу (4.7) и заменяя 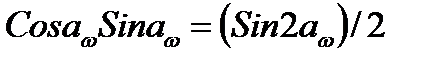 , получаем
, получаем
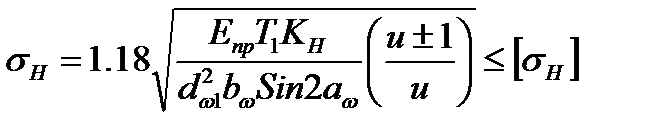 (4.10)
(4.10)
Данная формула определения контактных напряжений является классической. Гост 21354 даёт другую формулу, где ряд коэффициентов имеют иной вид, но она построена на базе формулы 4.10. В различных учебных пособиях и расчётных электронных программах эта формула также может быть представлена в ином виде и поэтому, если Вы выполняете расчет по одному из выбранных пособий, то значения коэффициентов необходимо принимать только из этого пособия.
Значения расчетных контактных напряжений одинаковы для шестерни и колеса. Поэтому расчет выполняют для того из колес пары, у которого меньше допускаемое напряжение [σн] (чаще это бывает колесо, а не шестерня).
Формулу (8.10) используют для проверочного расчета, когда все необходимые размеры и другие параметры передачи известны. При проектном расчете необходимо определить размеры передачи по заданным основным характеристикам: крутящему моменту Т1 или Т2и передаточному числу и. С этой целью формулу (4.10) решают относительно d1или а. Другие неизвестные параметры оценивают приближенно или выбирают по рекомендациям на основе накопленного опыта. В нашем случае принимаем: 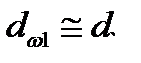 ,
, 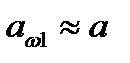 =20°, (sin 2a
=20°, (sin 2a 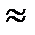 0,6428), Кv
0,6428), Кv 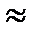 1,15 (этот коэффициент зависит от окружной скорости и, которая пока неизвестна, поэтому принято некоторое среднее значение — см. табл. 4.2). При этом из составляющих коэффициента Кн [см. формулу (4.4)] остается только Кнβ . Далее обозначаем
1,15 (этот коэффициент зависит от окружной скорости и, которая пока неизвестна, поэтому принято некоторое среднее значение — см. табл. 4.2). При этом из составляющих коэффициента Кн [см. формулу (4.4)] остается только Кнβ . Далее обозначаем 
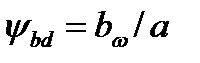 — коэффициент ширины шестерни относительно диаметра. Подставляя в формулу (4.10) и решая относительно d1, находим:
— коэффициент ширины шестерни относительно диаметра. Подставляя в формулу (4.10) и решая относительно d1, находим:
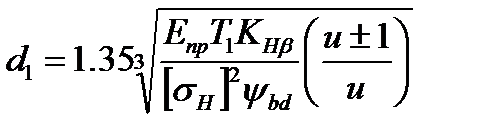 (4.11)
(4.11)
Решая относительно межосевого расстояния a, заменяем 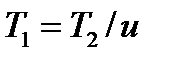 ;
; 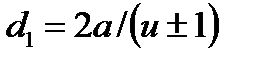 и вводим
и вводим 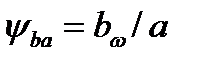 - коэффициент ширины колеса относительно межосевого расстояния. После преобразований с учётом зависимости
- коэффициент ширины колеса относительно межосевого расстояния. После преобразований с учётом зависимости 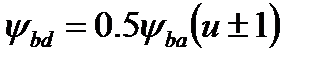 (4.12) ,
(4.12) ,
получим 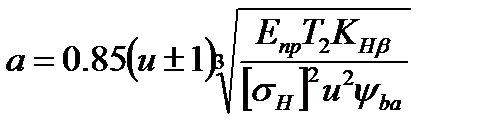 . (4.13)
. (4.13)
При расчёте передач с цилиндрическими зубчатыми колёсами чаще используют формулу (4.13) , так как габариты передачи определяет преимущественно межосевое расстояние.
Ниже приводятся рекомендуемые значения стандартизированного межосевого расстояния и рекомендуемые передаточные числа редукторов.
Стандартные межосевые расстояния aw:
1-й ряд —40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400...
2-й ряд—140, 180, 225, 280, 355, 450...
Стандартные значения 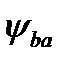 : 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8; 1,0; 1,25.
: 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8; 1,0; 1,25.
Стандартные номинальные передаточные числа u:
1-й ряд— 1,0; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0;
2-й ряд— 1,12; 1,4, 1,8; 2,24; 2,8; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2 (допускаемое отклонение ±4%).
Выбор модуля и числа зубьев. В формуле (8.10) модуль и число зубьев непосредственно не участвуют. Они входят в эту формулу косвенно через d1, который определяется произведением mz1. Из этого следует, что значение контактных напряжений 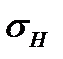 не зависит от модуля или числа зубьев в отдельности, а определяется только их произведениями или диаметрами колес. По условиям контактной прочности при данном d1 передачи может быть сколь угодно малым, лишь бы соблюдалось равенство mz1=d1.
не зависит от модуля или числа зубьев в отдельности, а определяется только их произведениями или диаметрами колес. По условиям контактной прочности при данном d1 передачи может быть сколь угодно малым, лишь бы соблюдалось равенство mz1=d1.
Минимально допускаемое значение модуля можно определить из условий прочности зубьев на изгиб. Однако при таком расчете в большинстве случаев получают зацепления с очень мелкими зубьями, применение которых практически ограничено. Поэтому значение тобычно выбирают, ориентируясь на рекомендации, выработанные практикой, и затем проверяют на изгиб. В этих рекомендациях учитывают следующее.
Мелкомодульные колеса с большим числом зубьев предпочтительны по условиям плавности хода передачи (увеличивается 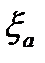 ) и экономичности. При малых т уменьшаются потери на трение (уменьшается скольжение), сокращается расход материала (уменьшается наружный диаметр) и экономится станочное время нарезания зубьев (уменьшается объем срезаемого материала).
) и экономичности. При малых т уменьшаются потери на трение (уменьшается скольжение), сокращается расход материала (уменьшается наружный диаметр) и экономится станочное время нарезания зубьев (уменьшается объем срезаемого материала).
Крупномодульные колеса с большим объемом зубьев дольше противостоят износу, могут работать длительное время после начала выкрашивания, менее чувствительны к перегрузкам и неоднородности материала (дефекты литья и т. п.). При мелком модуле возрастают требования к точности и жесткости передачи, так как увеличивается возможность поломки зубьев вследствие концентрации нагрузки , в особенности при перегрузках.
Практически рекомендуется принимать модуль зацепления в пределах 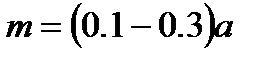 и стремиться к меньшему его значению.
и стремиться к меньшему его значению.
Расчет прочности зубьев по напряжениям изгиба. Зуб имеет сложное напряженное состояние. Наибольшие напряжения изгиба образуются у корня зуба в зоне перехода эвольвенты в галтель. Здесь же наблюдаются концентрация напряжений. Для того чтобы по возможности просто получить основные расчетные зависимости и уяснить влияние основных параметров на прочность зубьев, рассмотрим вначале приближенный расчет, а затем введем 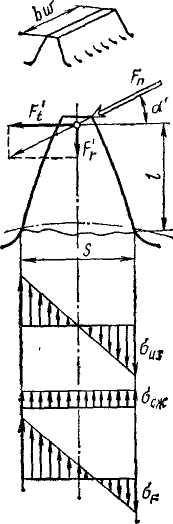 поправки в виде соответствующих коэффициентов. Допустим следующее (рис. 4.12):
поправки в виде соответствующих коэффициентов. Допустим следующее (рис. 4.12):
Вся нагрузка зацепления передается одной зубьев и приложена к вершине зуба. Практика подтверждает, что этот худший случай справедлив для 7-й, 8-й и более низких степеней точности, ошибки изготовления которых, не могут гарантировать наличие двухпарного зацепления. Например, ошибки шага приводят к тому, что зубья начинают зацепляться вершинами еще до выхода на линию зацепления. При этом вместо теоретического двухпарного зацепления будет однопарное. Зуб рассматриваем как консольную балку, для которой справедлива гипотеза плоских сечений или методы сопротивления материалов. Фактически зуб подобен выступу, у которого размеры поперечного сечения соизмеримы с размерами высоты. Точный расчет напряжений в таких элементах выполняют методами теории упругости. Результаты точного расчета используют для исправления приближенного расчета путем введения теоретического коэффициента концентрации напряжений (см. ниже). На расчетной схеме (см. рис. 4.12):
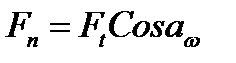 - см. формулу (4.6),
- см. формулу (4.6),
Где Ft – окружная сила, a – угол, определяющий направление нормальной силы Fn к оси симметрии зуба. Угол а/ несколько больше угла зацепления 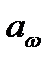 .
.
Силу 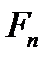 переносят по линии действия на ось симметрии зуба и раскладывают на составляющие
переносят по линии действия на ось симметрии зуба и раскладывают на составляющие
| Рис. 4.12 |
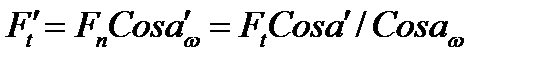
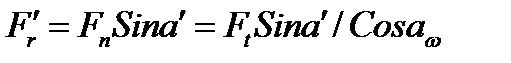
Напряжение в опасном сечении, расположенном вблизи хорды основной окружности 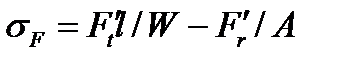 , где
, где
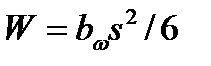 - момент сопротивления сечения при изгибе,
- момент сопротивления сечения при изгибе, 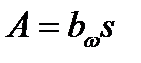 - площадь сечения. Величины bω , s , l - показаны на рис. 4.12.
- площадь сечения. Величины bω , s , l - показаны на рис. 4.12.
Знак (-) в формуле указывает, что за расчётные напряжения принимают напряжения на растянутой стороне зуба, так как на практике именно здесь возникают трещины усталостного порядка ( для чугуна и стали растяжение опаснее сжатия).
Значения l и s неудобны для расчётов и их заменяют на безразмерные коэффициенты 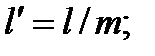 и
и 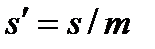 . Подставляя принятые обозначения, и вводя уточняющие поправки окончательно получим
. Подставляя принятые обозначения, и вводя уточняющие поправки окончательно получим
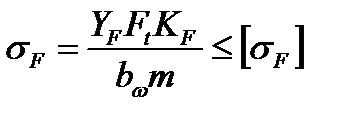 (4.14) , где
(4.14) , где 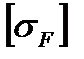 - допускаемое напряжение изгиба.
- допускаемое напряжение изгиба.
Величина YF - вбирает в себя все уточнения, поправки и конкретные значения и называется коэффициент формы зуба.Процесс вычисления данного коэффициента весьма трудоёмкий его значения в зависимости от числа зубьев на колесе или шестерне обязательно приводятся в справочной литературе по расчёту зубчатых передач.
KF – коэффициент нагрузки при расчёте на изгиб. Он учитывает точность изготовления и сборки передачи, условия её работы и выбирается по справочной литературе. На этапе проектного расчёта обычно принимают KF =1,5.
Если решить формулу (4.14) относительно модуля : 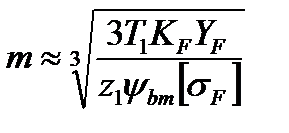 (4.15)
(4.15)
Здесь 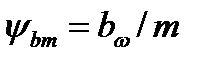 , z1 – число зубьев шестерни, Т1 – крутящий момент на шестерне.
, z1 – число зубьев шестерни, Т1 – крутящий момент на шестерне.
Дата добавления: 2015-11-28; просмотров: 3813;
