Кинетическая энергия системы
Кинетической энергией системы называется скалярная величина, равная сумме кинетических энергий всех точек системы:
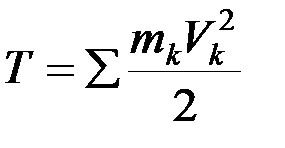 .
.
Вычислим кинетическую энергию при различных видах движения твердого тела.
Поступательное движение.В этом случае все точки движутся с одинаковыми скоростями, равными скорости центра масс – 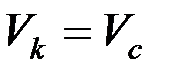 :
:
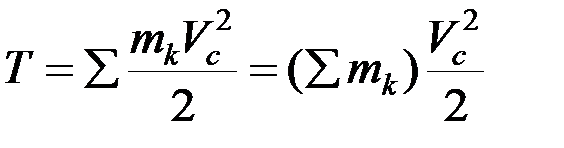 ,
,
следовательно, 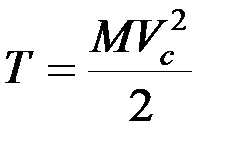 .
.
Вращательное движение.Пусть тело вращается относительно оси Оz с угловой скоростью w, тогда:
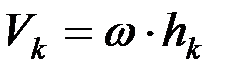 ,
,
где 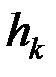 – расстояние от точки до оси вращения, w – угловая скорость. Тогда
– расстояние от точки до оси вращения, w – угловая скорость. Тогда
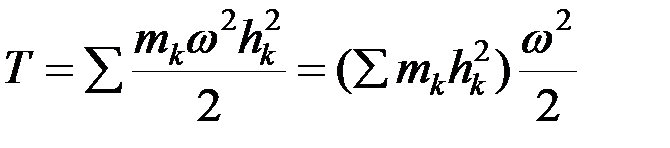 ,
,
следовательно, 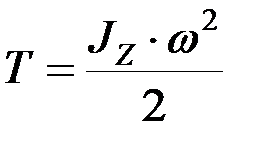 .
.
Плоскопараллельное движение.При этом движении все точки тела совершают вращательное движение вокруг оси, проходящей через мгновенный центр скоростей, следовательно
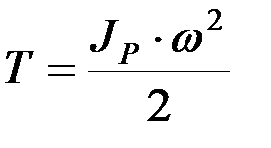 ,
,
где 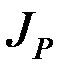 – момент инерции тела относительно оси, проходящей через МЦС.
– момент инерции тела относительно оси, проходящей через МЦС. 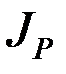 – величина переменная, т.к. положение мгновенного центра скоростей (точки Р) в каждый момент времени меняется. Выразим
– величина переменная, т.к. положение мгновенного центра скоростей (точки Р) в каждый момент времени меняется. Выразим 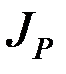 через
через 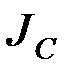 (момент инерции относительно параллельной оси, проходящей через центр масс). По теореме Гюйгенса,
(момент инерции относительно параллельной оси, проходящей через центр масс). По теореме Гюйгенса,
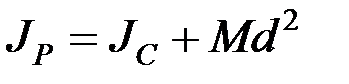 ,
,
где d = PC, тогда w d = w PC = VС,
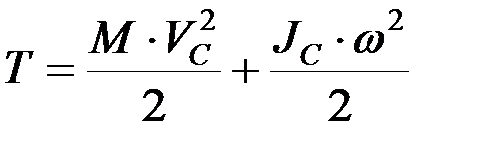 .
.
При плоскопараллельном движении кинетическая энергия тела равна энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг центра масс.
Эта теорема является частным случаем более общей теоремы, доказанной Кенигом (1751 г.).
Дата добавления: 2015-12-26; просмотров: 696;
