Индивидуальные и общие индексы
Индивидуальные индексы характеризуют изменение отдельных элементов той или иной совокупности. Индивидуальные индексы представляют собой относительные величины динамики, выполнения плана, сравнения, и их расчет не требует знания специальных правил.
В зависимости от экономического назначения индивидуальные индексы бывают физического объема продукции, себестоимости, цен, трудоемкости и т.д.
При расчете индексов используются общепринятые условные обозначения:
q1 и qo - физический объем продукции соответственно в отчетном и в базисном периодах;
p1 и po - цена единицы продукции соответственно в отчетном и в базисном периодах;
z1 и zo - себестоимость единицы продукции соответственно в отчетном и в базисном периодах;
t1 и to - затраты труда (рабочего времени) на единицу продукции соответственно в отчетном и в базисном периодах.
Индивидуальный индекс физического объема продукции:
.
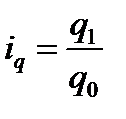Индивидуальный индекс цен:
.
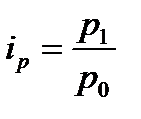Индивидуальный индекс себестоимости:
.
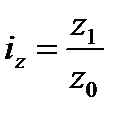Индивидуальный индекс производительности труда:
.
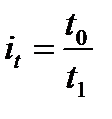Индивидуальный индекс производительности труда находится в результате деления величины показателя в базисном периоде на величину в текущем, т.к. между количеством продукции, произведенной в единицу времени (v), и затратами рабочего времени на производство единицы продукции (t) существует обратно пропорциональная зависимость:
.
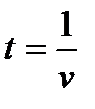В знаменателе может быть не только значение показателя за какой-то предыдущий период, но и плановое, нормативное, эталонное.
Пример
Имеются следующие данные о продаже и цене изделий в магазине города (табл. 11.1). Определить индивидуальные индексы физического объема продукции (объема продаж) и индивидуальные индексы цен.
Таблица 11.1 – Объем продаж плащей и курток
| Наименование товара | Объем продаж, шт. | Цена 1 изд., тыс. руб. | Расчетные графы | |||
| Индивидуальные индексы | ||||||
| физического объема | цен | |||||
| q0 | q1 | p0 | p1 | iq = q1 / q0 | ip = p1 / p0 | |
| Плащи жен. | 1,5 | 1,7 | 0,820 | 1,133 | ||
| Куртки муж. | 0,8 | 0,9 | 1,053 | 1,125 |
Таким образом, объем продаж плащей в 2013 г. по сравнению с 2012 г. уменьшился на 18% (82-100), а курток увеличился на 5,3% (105,3-100); цена плащей увеличилась на 13,3% (113,3-100), а курток - на 12,5% (112,5-100).
Общие (сводные) индексы – сложные относительные показатели, которые характеризуют среднее изменение социально-экономических явлений, состоящих из непосредственно несоизмеримых элементов. Общие индексы строят для количественных (объемных) и качественных показателей. В зависимости от цели исследования и наличия исходных данных используют различную форму построения общих индексов: агрегатную или среднюю.
Агрегатные индексы
Исходной формой сводного индекса является агрегатная. Агрегатная форма сводного индекса является основной. Агрегатный индекс - это сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из непосредственно несоизмеримых элементов. При расчете агрегатного индекса для разнородной совокупности находят такой общий показатель, в котором можно объединить все ее элементы.
Агрегатные индексы состоят из двух элементов: индексируемой величины и веса индекса. Индексируемая величина - это показатель, изменение которого изучается (отражает индекс). Вес индекса – это величина, служащая для целей соизмерения индексируемых величин. В числителе и знаменателе он принимается на уровне одного периода (отчетного или базисного). В практике статистики соблюдается правило: индексы объемных показателей строятся по весам базисного периода, индексы качественных показателей строятся по весам текущего периода. При этом выбор веса (соизмерителя) должен осуществляться с учетом сущности изучаемых явлений, а показатели, полученные в результате взвешивания, должны быть не просто соизмеримы, но и сохранять определенное экономическое содержание. Это позволяет определять сумму экономического эффекта, т.е. изменение изучаемого явления в абсолютном выражении. Рассмотрим основные агрегатные индексы, используемые в статистике.
Агрегатный индекс стоимости продукции (товарооборота) рассчитывается по формуле:
.
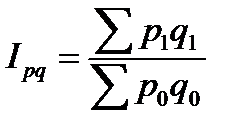Такой индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции.
Если из значения индекса стоимости вычесть 100% (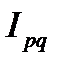 
-100), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным.
Разность числителя и знаменателя (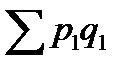 
- 
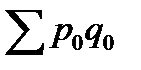) показывает, на сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным.
На величину данного индекса оказывают влияние как изменение цен, так и изменение объемов реализации. Чтобы оценить изменение только цен (индексируемой величины) или только физического объема продукции, необходимо другой показатель (вес индекса) зафиксировать на каком-либо постоянном уровне.
Агрегатный индекс физического объема продукции рассчитывается по формуле:
.
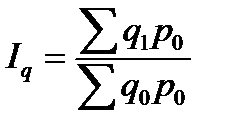Индекс физического объема продукции показывает во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объема ее производства или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения физического объема ее производства.
Если из значения индекса физического объема продукции вычесть 100% (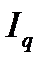 
-100), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным из-за роста (снижения) физического объема ее производства.
Разность числителя и знаменателя (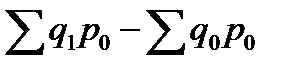 
) показывает на сколько рублей изменилась стоимость продукции в отчётном периоде по сравнению с базисным в результате изменения физического объема. Изменение цен не влияет на величину индекса.
Агрегатный индекс цен рассчитывается по формуле:
.
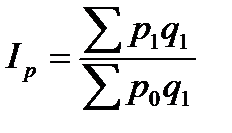Этот индекс характеризует изменение цен на различные товары, реализованные в текущем периоде. Индекс цен показывает во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен, или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения цен.
Если из значения индекса цен вычесть 100% (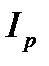 
-100), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным из-за изменения цен.
Разность числителя и знаменателя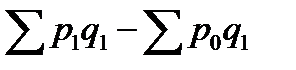 
показывает на сколько рублей изменилась стоимость продукции в отчётном периоде по сравнению с базисным в результате изменения цен. Изменение количества произведенной продукции не влияет на величину индекса.
Разность между числителем и знаменателем показывает экономию, или дополнительные затраты населения, в результате снижения или повышения цен.
Между рассчитанными индексами существует следующая взаимосвязь:
Ip·Iq = Ipq .
Пример
Определить по имеющимся данным (табл. 11.2) сводный индекс физического объёма продукции; сводный индекс цен; сводный индекс стоимости продукции (товарооборота); абсолютный прирост (уменьшение) товарооборота в 2013 году по сравнению с 2012 – всего, в т. ч. за счет изменения физического объёма продукции и цен. Показать взаимосвязь между исчисленными индексами.
Таблица 11.2 – Объем продаж плащей и курток
| Наименование товара | Продано изделий, шт. | Цена 1 изд., тыс. руб. | Расчетные графы | ||||
| 
| 
| |||||
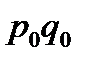
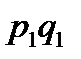
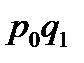
| q0 | q1 | p0 | p1 | ||||
| Плащи жен. | 1,5 | 1,7 | 150,0 | 139,4 | 123,0 | ||
| Куртки муж. | 0,8 | 0,9 | 45,6 | 54,0 | 48,0 | ||
| Итого | - | - | - | - | 195,6 | 193,4 | 171,0 |
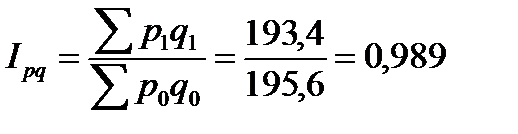или 98,9%
Индекс показывает, что стоимость продукции в 2013 году сократилась по сравнению с 2012 г. на 1,1% (98,9-100) или на 2,2 тыс. руб. (193,4-195,6).
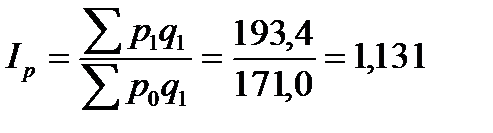или 113,1%
Индекс показывает, что стоимость продукции в 2013 году по сравнению с 2012 г. увеличилась в результате роста цен на 13,1% (113,1-100) или на 22,4 тыс. руб. (193,4-171,0).
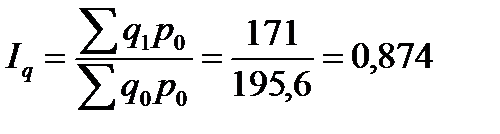или 87,4 %
Индекс показывает, что стоимость продукции в 2013 году по сравнению с 2012 г. сократилась в результате снижения объема продаж на 12,6% (87,4-100) или на 24,6 тыс. руб. (171,0-195,6)
Проверка: 1,131·0,874 = 0,989
Аналогично строятся индексы для показателей, которые являются произведением двух сомножителей: издержек производства (произведение себестоимости единицы продукции на количество продукции); затрат времени на производство всей продукции (произведение затрат времени на производство единицы продукции на количество выработанной продукции).
Агрегатный индекс издержек производства:
.
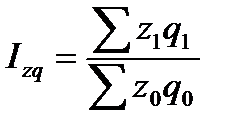Агрегатный индекс себестоимости:
.
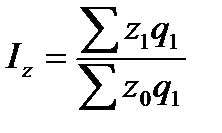Агрегатный индекс физического объема продукции:
.
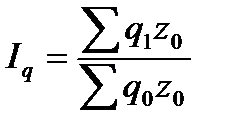Производительность трудаможет быть измерена количеством продукции, производимой в единицу времени (выработка) или затратами рабочего времени на производство единицы продукции (трудоемкость).
Агрегатный индекс затрат времени на производство продукции:
.
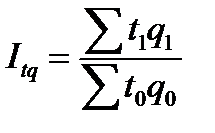Агрегатный индекс производительности труда:
.
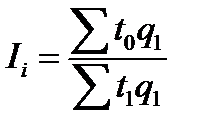Агрегатный индекс физического объема продукции:
.
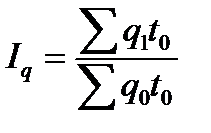Средние индексы
Второй формой сводного индекса являются средние индексы. Их применяют, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если отсутствуют данные о ценах, но имеется информация о стоимости продукции в текущем периоде и известны индивидуальные индексы цен по каждому товару, то общий индекс цен как агрегатный определить нельзя, однако возможно исчислить его как средний из индивидуальных.
Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. В практике статистики используют средний арифметический и средний гармонический индексы.
Предположим, мы располагаем данными о стоимости проданной продукции в текущем периоде (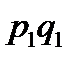 
) и индивидуальными индексами цен 
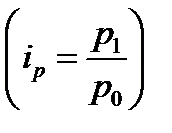, т.е. знаем, как изменились цены на отдельные товары. Тогда в знаменателе сводного индекса цен 
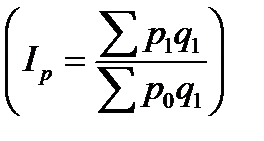можно использовать следующую замену: 
.
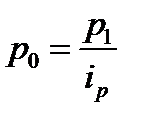Таким образом, сводный индекс цен будет выражен в форме средней гармонической из индивидуальных индексов:
.
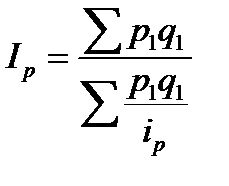Средний гармонический индекс тождественен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса.
Пример
Определить сводный индекс тарифов по имеющимся данным (табл. 11.3)
Таблица 11.3 – Доходы от перевозки грузов
| Род груза | Сумма доходов в текущем периоде, тыс. руб. (p1q1) | Изменение тарифа в текущем периоде по сравнению с базисным, % | Расчетные графы | |
| 
| |||
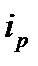
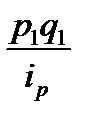
| Лесоматериалы Нефтепродукты Торф | +4,0 +2,3 -0,8 | 1,04 1,023 0,992 | ||
| Итого | – | – |
Вычислим средний гармонический индекс:
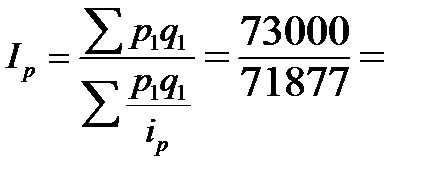1,016 или 101,6 %.
Таким образом, тарифы по данной группе грузов в текущем периоде по сравнению с базисным в среднем возросли на 1,6 %.
Средний арифметический индекс тождественен агрегатному индексу, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса.
При расчете сводного индекса физического объема продукции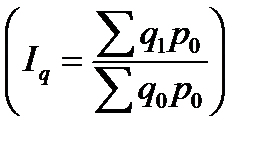 
можно использовать среднюю арифметическую форму. При этом в числителе производится замена 
= 
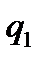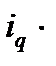
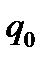. Тогда индекс примет вид:
.
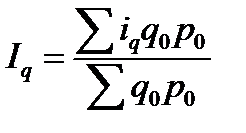Пример
Определить сводный индекс объема перевозок по следующим данным (табл. 11.4):
Таблица 11.4 – Доходы от перевозки грузов
| Род груза | Доходы от перевозок в базисном периоде,
тыс. руб. (  )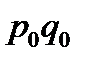
| Изменение объема перевозок в текущем периоде по сравнению с базисным, % | Расчетные графы | |
|   
| |||
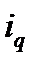
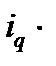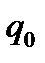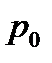
| Кирпич Цемент Удобрения | –6,4 –8,2 +1,3 | 0,936 0,918 1,013 | ||
| Итого | – | – |
Рассчитаем средний арифметический индекс:
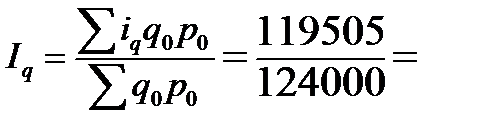0,964 или 96,4 %.
Таким образом, объем перевозок по данной группе грузов в среднем снизился на 3,6 %.
11.5. Система индексов: цепные и базисные
Система используется при изучении динамики социально-экономических явлений за некоторый интервал времени, включающий более двух периодов времени. Системой индексов называется ряд последовательно построенных индексов. Такие системы характеризуют изменения, происходящие в изучаемом явлении в течение исследуемого периода времени.
В зависимости от базы сравнения системы индексов бывают базисными и цепными (см. рис. 11.1). Система базисных индексов - это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения, т.е. в знаменателе всех индексов находится индексируемая величина базисного периода. Система цепных индексов - это ряд индексов одного и того же явления, вычисленных с меняющейся от индекса к индексу базой сравнения. В экономико-статистических исследованиях выбор системы индексов (базисные или цепные) проводится в зависимости от цели анализа.
Системы цепных и базисных индексов могут быть построены для индивидуальных и общих индексов. Системы индивидуальных индексов стоимости продукции, физического объема продукции и цен (табл. 11.5) просты по построению. Аналогично им строятся системы индивидуальных индексов и для других показателей.
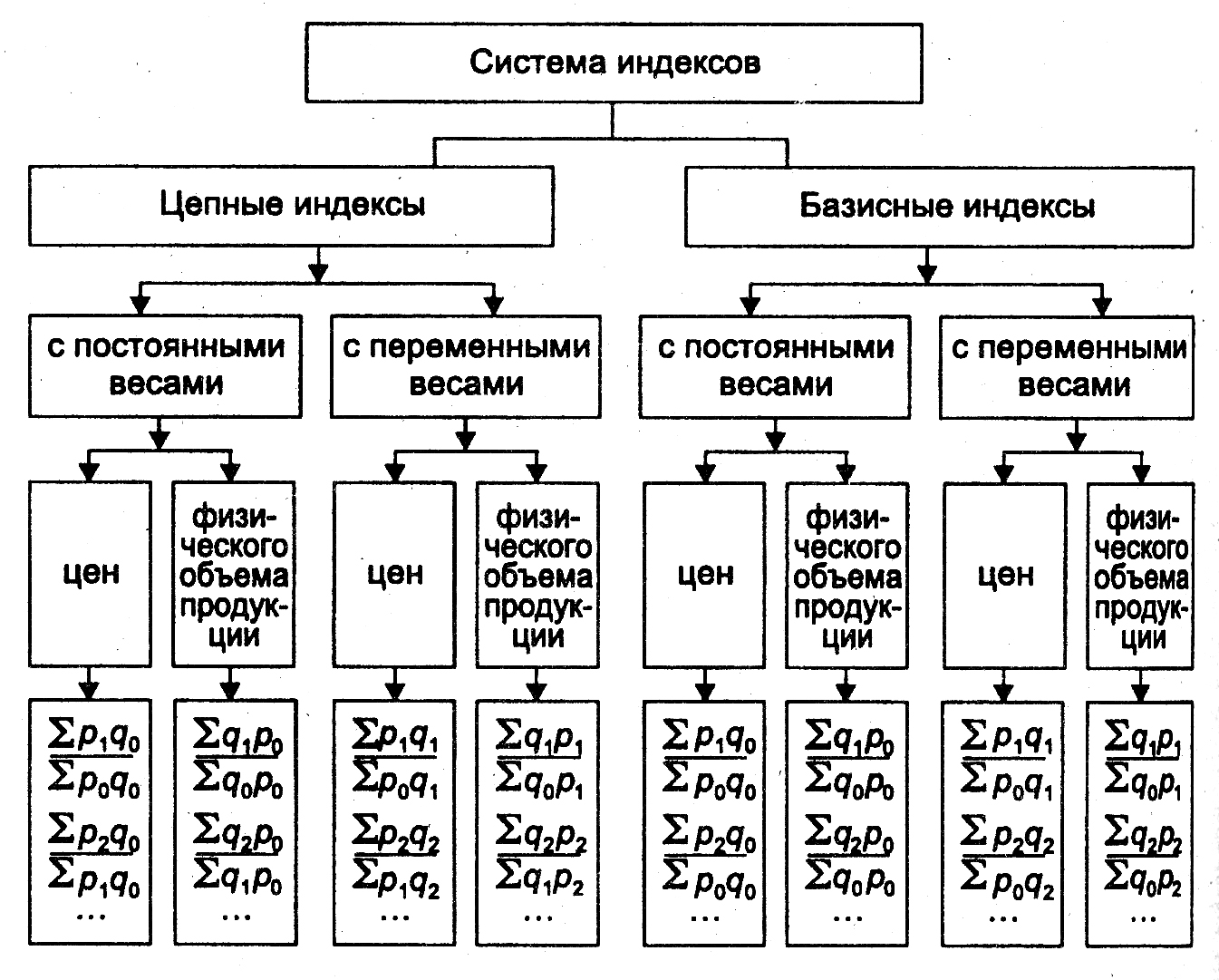
Рис. 11.1. Способы построения системы индексов
Таблица 11.5 – Система индивидуальных индексов
Между цепными и базисными индексами существуют различные виды связей. Если известны цепные индексы, то путем их последовательного перемножения можно получить базисные индексы. Например,
.
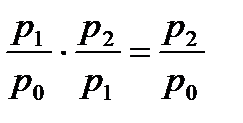Зная последовательные значения базисных индексов, легко рассчитать на их основе цепные индексы:
.
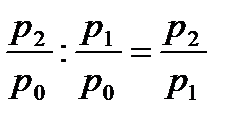Рассмотрим пример построения система базисных и цепных индексов для агрегатных индексов стоимости продукции (товарооборота):
Цепные индексы: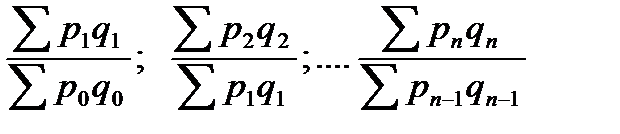 
Базисные индексы: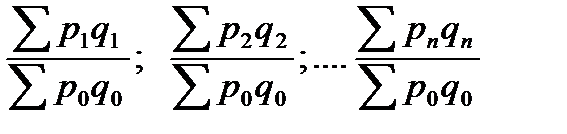 
Формирование системы индексов, например, цен или физического объема, отличается от уже рассмотренных. Это связано с тем, что при построении систем этих индексов можно использовать постоянные и переменные веса.
Системой индексов с постоянными весами называется система сводных индексов одного и того же явления, вычисленных с весами, не меняющимися при переходе от одного индекса к другому. Постоянные веса позволяют исключить влияние изменения структуры на величину индекса. Система индексов с переменными весами представляет собой систему сводных индексов одного и того же явления, вычисленных с весами, последовательно меняющимися от одного индекса к другому. Переменные веса – это веса отчетного периода. Рассмотрим систему индексов на примере сводного индекса цен, рассчитываемого за три периода:
1. Цепные индексы цен с переменными весами:
; 
; 
.
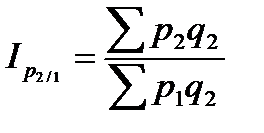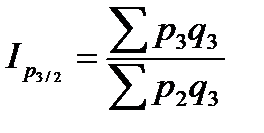2. Цепные индексы цен с постоянными весами:
; 
; 
.
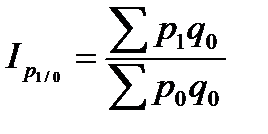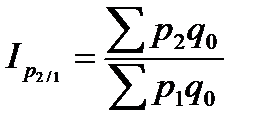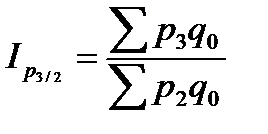3. Базисные индексы цен с переменными весами:
; 
; 
.
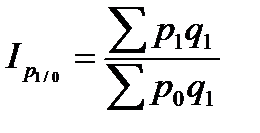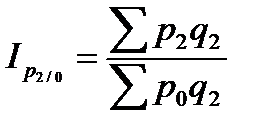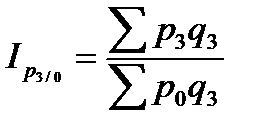4. Базисные индексы цен с постоянными весами:
; 
; 
.
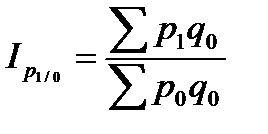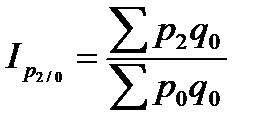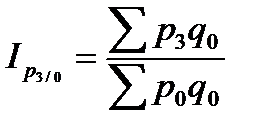Дата добавления: 2015-12-26; просмотров: 15753;